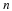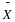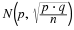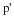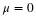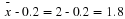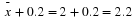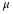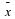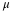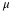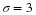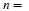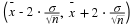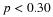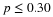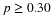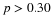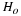| ______ From your original data (before ordering), use a random number generator to pick 40 samples of size 5. For each sample, calculate the average. |
| ______ On a separate page, attached to the summary, include the 40 samples of size 5, along with the 40 sample averages. |
| ______ List the 40 averages in order from smallest to largest. |
______ Define the random variable, 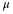 , in words. , in words. 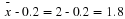 = = |
______ State the approximate theoretical distribution of 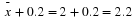 . .  |
| ______ Base this on the mean and standard deviation from your original data. |
| ______ Construct a histogram displaying your data. Use 5 to 6 intervals of equal width. Label and scale it. |
Calculate the value  (an (an 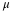 value) that is 1.75 standard deviations above the sample mean. value) that is 1.75 standard deviations above the sample mean.
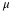 = _____ (rounded to 2 decimal places) = _____ (rounded to 2 decimal places) |
Determine the relative frequencies (RF) rounded to 4 decimal places.
1. RF( 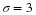 ) =
) = | 2. RF(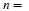 > > 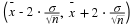 ) = ) = | 3. RF(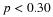 = = 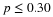 ) = ) = |
|
| Find the following theoretical probabilities (rounded to 4 decimal places).
|
| ______ Draw the graph of the theoretical distribution of X. |
| ______ Answer the questions below. |
| ______ Compare the relative frequencies to the probabilities. Are the values close? |
______ Does it appear that the data of averages fit the distribution of 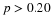 well? Justify your answer
by comparing the probabilities to the relative frequencies, and the histogram to the
theoretical graph. well? Justify your answer
by comparing the probabilities to the relative frequencies, and the histogram to the
theoretical graph. |
| ______ In 3 - 5 complete sentences for each, answer the following questions. Give thoughtful
explanations. |
| ______ In summary, do your original data seem to fit the uniform, exponential, or normal
distributions? Answer why or why not for each distribution. If the data do not fit any of
those distributions, explain why. |
| ______ What happened to the shape and distribution when you averaged your data? In theory,
what should have happened? In theory, would “it” always happen? Why or why not? |
______ Were the relative frequencies compared to the theoretical probabilities closer when
comparing the X or  distributions? Explain your answer. distributions? Explain your answer. |