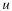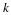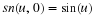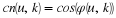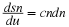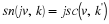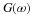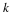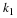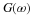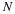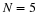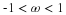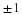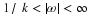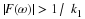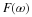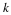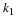Definition of the Fourier Series
We assume that the signal x(t) to be analyzed is well described by a
real or complex valued function of a real variable t defined over a
finite interval {0≤t≤T}. The trigonometric series expansion
of x(t) is given by
where xk(t)=cos(2πkt/T) and yk(t)=sin(2πkt/T) are the
basis functions for the expansion. The energy or power in an electrical,
mechanical, etc. system is a function of the square of voltage, current,
velocity, pressure, etc. For this reason, the natural setting for a
representation of signals is the Hilbert space of L2[0,T]. This modern
formulation of the problem is developed in 6, 11. The
sinusoidal basis functions in the trigonometric expansion form a complete
orthogonal set in L2[0,T]. The orthogonality is easily seen from inner
products
and
where δ(t) is the Kronecker delta function with
δ(0)=1 and δ(k≠0)=0. Because of this, the kth
coefficients in the series can be found by taking the inner product of
x(t) with the kth basis functions. This gives for the coefficients
and
where T is the time interval of interest or the period of
a periodic signal. Because of the orthogonality of the basis functions, a
finite Fourier series formed by truncating the infinite series is an
optimal least squared error approximation to x(t). If the finite series
is defined by
the squared error is
which is minimized over all a(k) and b(k) by
Equation 1.4 and Equation 1.5. This is an extraordinarily important
property.
It follows that if x(t)∈L2[0,T], then the series converges to
x(t) in the sense that ε→0 as N→∞6, 11. The question of point-wise convergence is
more difficult. A sufficient condition that is adequate for most
application states: If f(x) is bounded, is piece-wise continuous, and
has no more than a finite number of maxima over an interval, the Fourier
series converges point-wise to f(x) at all points of continuity and to
the arithmetic mean at points of discontinuities. If f(x) is
continuous, the series converges uniformly at all points
11, 8, 3.
A useful condition 6, 11 states that if x(t)
and its derivatives through the qth derivative are defined and have
bounded variation, the Fourier coefficients a(k) and b(k)
asymptotically drop off at least as fast as 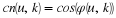 as k→∞. This ties global rates of convergence of the
coefficients to local smoothness conditions of the function.
as k→∞. This ties global rates of convergence of the
coefficients to local smoothness conditions of the function.
The form of the Fourier series using both sines and cosines makes
determination of the peak value or of the location of a particular
frequency term difficult. A different form that explicitly gives the peak
value of the sinusoid of that frequency and the location or phase shift of
that sinusoid is given by
and, using Euler's relation and the usual electrical
engineering notation of 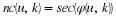 ,
,
(1.9)
ejx
=
cos
(
x
)
+
j
sin
(
x
)
,
the complex exponential form is obtained as
where
The coefficient equation is
The coefficients in these three forms are related by
(1.13)
|
d
|
2
=
|
c
|
2
=
a2
+
b2
and
It is easier to evaluate a signal in terms of c(k) or d(k) and
θ(k) than in terms of a(k) and b(k). The first two are polar
representation of a complex value and the last is rectangular. The
exponential form is easier to work with mathematically.
Although the function to be expanded is defined only over a specific
finite region, the series converges to a function that is defined over the
real line and is periodic. It is equal to the original function over the
region of definition and is a periodic extension outside of the region.
Indeed, one could artificially extend the given function at the outset and
then the expansion would converge everywhere.