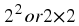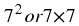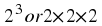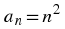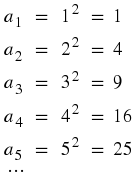In earlier grades you saw patterns in the form of pictures and numbers. In this chapter, we learn more about the mathematics of patterns. Patterns are recognisable as repetitive sequences and can be found in nature, shapes, events, sets of numbers and almost everywhere you care to look. For example, seeds in a sunflower, snowflakes, geometric designs on quilts or tiles, the number sequence 0, 4, 8, 12, 16,....
Can you spot any patterns in the following lists of numbers?
2; 4; 6; 8; 10; ...
1; 2; 4; 7; 11; ...
1; 4; 9; 16; 25; ...
5; 10; 20; 40; 80; ...
Numbers can have interesting patterns. Here we list the most common patterns and how they are made.
Examples:
1,4,7,10,13,16,19,22,25,... This sequence has a difference of 3 between each number. The pattern is continued by adding 3 to the last number each time.
3,8,13,18,23,28,33,38,... This sequence has a difference of 5 between each number. The pattern is continued by adding 5 to the last number each time.
2,4,8,16,32,64,128,256,... This sequence has a factor of 2 between each number. The pattern is continued by multiplying the last number by 2 each time.
3,9,27,81,243,729,2187,... This sequence has a factor of 3 between each number. The pattern is continued by multiplying the last number by 3 each time.
1 , 3 , 6 , 10 , 15 , 21 , 28 , 36 , 45 , . . .
This sequence is generated from a pattern of dots which form a triangle. By adding another row of dots (with one more dot in each row than in the previous row) and counting all the dots, we can find the next number of the sequence.
1 , 4 , 9 , 16 , 25 , 36 , 49 , 64 , 81 , . . .
The next number is made by squaring the number of the position in the pattern.
The second number is 2 squared (
).
The seventh number is 7 squared (
) etc.
1 , 8 , 27 , 64 , 125 , 216 , 343 , 512 , 729 , . . .
The next number is made by cubing the number of the position in the pattern.
The second number is 2 cubed (
).
The seventh number is 7 cubed (
) etc.
0 , 1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , . . .
The next number is found by adding the two numbers before it together. The 2 is found by adding the two numbers in front of it (1 + 1). The 21 is found by adding the two numbers in front of it (8 + 13). The next number in the sequence above would be 55 (21 + 34).
Can you figure out the next few numbers?
Figure 1.1. Khan Academy video on Number Patterns - 1
Exercise 1.1.1. Study Table (Go to Solution)
Say you and 3 friends decide to study for Maths, and you are seated at a square table. A few minutes later, 2 other friends join you and would like to sit at your table and help you study. Naturally, you move another table and add it to the existing one. Now 6 of you sit at the table. Another 2 of your friends join your table, and you take a third table and add it to the existing tables. Now 8 of you can sit comfortably.
Figure 1.2.
Examine how the number of people sitting is related to the number of tables.
Solution to Exercise 1.1.1. (Return to Exercise)
Tabulate a few terms to see if there is a pattern :
| Number of Tables, n | Number of people seated |
| 1 | 4 = 4 |
| 2 | 4 + 2 = 6 |
| 3 | 4 + 2 + 2 = 8 |
| 4 | 4 + 2 + 2 + 2 = 10 |
| ⋮ | ⋮ |
| n | 4 + 2 + 2 + 2 + ... + 2 |
We can see that for 3 tables we can seat 8 people, for 4 tables we can seat 10 people and so on. We started out with 4 people and added two each time. Thus, for each table added, the number of persons increased by 2.
Figure 1.3. Khan Academy video on Number Patterns
A sequence does not have to follow a pattern but when it does, we can often write down a formula to calculate the n th -term, a n . In the sequence
where the sequence consists of the squares of integers, the formula for the n th -term is
You can check this by looking at:
Therefore, using Equation 1.2, we can generate a pattern, namely squares of integers.
Exercise 1.2.1. Study Table continued .... (Go to Solution)
As before, you and 3 friends are studying for Maths, and you are seated at a square table. A few minutes later, 2 other friends join you and add another table to the existing one. Now 6 of you can sit together. A short time later 2 more of your friends join your table, and you add a third table to the existing tables. Now 8 of you can sit comfortably as shown:
Figure 1.4.
Find the expression for the number of people seated at n tables. Then, use the general formula to determine how many people can sit around 12 tables and how many tables are needed for 20 people.
It is also important to note the difference between n and a n . n can be compared to a place holder, while a n is the value at the place “held” by n . Like our “Study Table” example above, the first table (Table 1) holds 4 people. Thus, at place n = 1, the value of a 1 = 4 and so on:
| n | 1 | 2 | 3 | 4 | ... |
| a n | 4 | 6 | 8 | 10 | ... |
Find the general formula for the following sequences and then find a 10, a 50 and a 100:
2,5,8,11,14,...
0,4,8,12,16,...
2, – 1, – 4, – 7, – 10,...
The general term has been given for each sequence below. Work out the missing terms.
0;3;...;15;24 n 2 – 1
3;2;1;0;...; – 2 – n + 4
– 11;...; – 7;...; – 3 – 13 + 2n
Figure 1.5. Khan Academy video on Number Patterns - 2
In mathematics, a conjecture is a mathematical statement which appears to be true, but has not been formally proven to be true. A conjecture can be seen as an educated guess or an idea about a pattern.
For example: Make a conjecture about the next number based on the pattern 2;6;11;17 : ...
The numbers increase by 4, 5, and 6.
Conjecture: The next number will increase by 7. So, it will be 17 + 7 or 24.
Exercise 1.2.2. Number patterns (Go to Solution)
Consider the following pattern.
Add another two rows to the end of the pattern.
Make a conjecture about this pattern. Write your conjecture in words.
Generalise your conjecture for this pattern (in other words, write your conjecture algebraically).
Prove that your conjecture is true.
There are several special sequences of numbers:
Triangular numbers 1 , 3 , 6 , 10 , 15 , 21 , 28 , 36 , 45 , . . .
Square numbers 1 , 4 , 9 , 16 , 25 , 36 , 49 , 64 , 81 , . . .
Cube numbers 1 , 8 , 27 , 64 , 125 , 216 , 343 , 512 , 729 , . . .
Fibonacci numbers 0 , 1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , . . .
General formula is a n = a 1 + d · ( n – 1 ) where d is the common difference between terms and a n is the n th -term
Find the n th term for: 3,7,11,15,... Click here for the solution
Find the general term of the following sequences:
– 2,1,4,7,...
11,15,19,23,...
sequence with a 3 = 7 and a 8 = 15
sequence with a 4 = – 8 and a 10 = 10
The seating in a section of a sports stadium can be arranged so the first row has 15 seats, the second row has 19 seats, the third row has 23 seats and so on. Calculate how many seats are in the row 25. Click here for the solution
A single square is made from 4 matchsticks. Two squares in a row need 7 matchsti