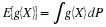We use the term m-function to designate a user-defined function as distinct from the basic MATLAB functions which are part of the MATLAB package. For example, the m-function minterm produces the specified minterm vector. An m-procedure (or sometimes a procedure) is an m-file containing a set of MATLAB commands which carry out a prescribed set of operations. Generally, these will prompt for (or assume) certain data upon which the procedure is carried out. We use the term m-program to refer to either an m-function or an m-procedure.
In addition to the m-programs there is a collection of m-files with properly formatted data which can be entered into the workspace by calling the file.
Although the m-programs were written for MATLAB version 4.2, they work for versions 5.1, 5.2, and 7.04. The latter versions offer some new features which may make more efficient implementation of some of the m-programs, and which make possible some new ones. With one exception (so noted), these are not explored in this collection.
Utilization of MATLAB resources is made possible by a systematic analysis of some features of the basic probability model. In particular, the minterm analysis of logical (or Boolean) combinations of events and the analysis of the structure of simple random variables with the aid of indicator functions and minterm analysis are exploited.
A number of standard features of MATLAB are utilized extensively. In addition to standard matrix algebra, we use:
Array arithmetic. This involves element by element calculations. For example,
if a, b are matrices of the same size, then a.*b is the matrix obtained
by multiplying corresponding elements in the two matrices to obtain a new matrix of
the same size.
Relational operations, such as less than, equal, etc. to obtain zero-one matrices with ones at element positions where the conditions are met.
Logical operations on zero-one matrices utilizing logical operators and, or,
and not, as well as certain related functions such as any, all, not,
find, etc.
Note. Relational operations and logical operations produce zero-one arrays, called logical
arrays, which MATLAB treats differently from zero-one numeric arrays. A rectangular array
in which some rows are logical arrays but others are not is treated as a numeric array.
Any zero-one rectangular array can be converted to a numeric array (matrix) by the command
A = ones(size(A)).*A,
Certain MATLAB functions, such as meshgrid, sum, cumsum, prod, cumprod are used repeatedly. The function dot for dot product does not work if either array is a logical array. If one of the pair is numeric, the command C = A*B' will work.
One of the most useful is a special sorting and consolidation operation implemented in the m-function csort. A standard problem arises when each of a non distinct set of values has an associated probability. To obtain the distribution, it is necessary to sort the values and add the probabilities associated with each distinct value. The following m-function achieves these operations: function [t,p] = csort(T,P). T and P are matrices with the same number of elements. Values of T are sorted and identical values are consolidated; values of P corresponding to identical values of T are added. A number of derivative functions and procedures utilize csort. The following two are useful.
function [t,p] = csort(T,P) % CSORT [t,p] = csort(T,P) Sorts T, consolidates P % Version of 4/6/97 % Modified to work with Versions 4.2 and 5.1, 5.2 % T and P matrices with the same number of elements % The vector T(:)' is sorted: % * Identical values in T are consolidated; % * Corresponding values in P are added. T = T(:)'; n = length(T); [TS,I] = sort(T); d = find([1,TS(2:n) - TS(1:n-1) >1e-13]); % Determines distinct values t = TS(d); % Selects the distinct values m = length(t) + 1; P = P(I); % Arranges elements of P F = [0 cumsum(P(:)')]; Fd = F([d length(F)]); % Cumulative sums for distinct values p = Fd(2:m) - Fd(1:m-1); % Separates the sums for these values
distinct.m
function y = distinct(T) determines and sorts the distinct
members of matrix T.
function y = distinct(T)
% DISTINCT y = distinct(T) Disinct* members of T
% Version of 5/7/96 Rev 4/20/97 for version 4 & 5.1, 5.2
% Determines distinct members of matrix T.
% Members which differ by no more than 10^{-13}
% are considered identical. y is a row
% vector of the distinct members.
TS = sort(T(:)');
n = length(TS);
d = [1 abs(TS(2:n) - TS(1:n-1)) >1e-13];
y = TS(find(d));
freq.m sorts the distinct members of a matrix, counts the number of occurrences of each value, and calculates the cumulative relative frequencies.
% FREQ file freq.m Frequencies of members of matrix
% Version of 5/7/96
% Sorts the distinct members of a matrix, counts
% the number of occurrences of each value, and
% calculates the cumulative relative frequencies.
T = input('Enter matrix to be counted ');
[m,n] = size(T);
[t,f] = csort(T,ones(m,n));
p = cumsum(f)/(m*n);
disp(['The number of entries is ',num2str(m*n),])
disp(['The number of distinct entries is ',num2str(length(t)),] )
disp(' ')
dis = [t;f;p]';
disp(' Values Count Cum Frac')
disp(dis)
dsum.mfunction y = dsum(v,w) determines and sorts the distinct
elements among the sums of pairs of elements of row vectors v and
w.
function y = dsum(v,w) % DSUM y = dsum(v,w) Distinct pair sums of elements % Version of 5/15/97 % y is a row vector of distinct % values among pair sums of elements % of matrices v, w. % Uses m-function distinct [a,b] = meshgrid(v,w); t = a+b; y = distinct(t(:)');
rep.mfunction y = rep(A,m,n) replicates matrix A, m times
vertically and n times horizontally. Essentially the same as the function repmat in
MATLAB version 5, released December, 1996.
function y = rep(A,m,n) % REP y = rep(A,m,n) Replicates matrix A % Version of 4/21/96 % Replicates A, % m times vertically, % n times horizontally % Essentially the same as repmat in version 5.1, 5.2 [r,c] = size(A); R = [1:r]'; C = [1:c]'; v = R(:,ones(1,m)); w = C(:,ones(1,n)); y = A(v,w);
elrep.mfunction y = elrep(A,m,n) replicates each element of
A, m times vertically and n times horizontally.
function y = elrep(A,m,n) % ELREP y = elrep(A,m,n) Replicates elements of A % Version of 4/21/96 % Replicates each element, % m times vertically, % n times horizontally [r,c] = size(A); R = 1:r; C = 1:c; v = R(ones(1,m),:); w = C(ones(1,n),:); y = A(v,w);
kronf.mfunction y = kronf(A,B) determines the Kronecker product
of matrices 
. Achieves the same result for full matrices as the MATLAB function
kron.
function y = kronf(A,B) % KRONF y = kronf(A,B) Kronecker product % Version of 4/21/96 % Calculates Kronecker product of full matrices. % Uses m-functions elrep and rep % Same result for full matrices as kron for version 5.1, 5.2 [r,c] = size(B); [m,n] = size(A); y = elrep(A,r,c).*rep(B,m,n);
colcopy.mfunction y = colcopy(v,n) treats row or column vector
v as a column vector and makes a matrix with n columns of v.
function y = colcopy(v,n) % COLCOPY y = colcopy(v,n) n columns of v % Version of 6/8/95 (Arguments reversed 5/7/96) % v a row or column vector % Treats v as column vector % and makes n copies % Procedure based on "Tony's trick" [r,c] = size(v); if r == 1 v = v'; end y = v(:,ones(1,n));
colcopyi.mfunction y = colcopyi(v,n) treats row or column
vector v as a column vector, reverses the order of the elements, and makes a
matrix with n columns of the reversed vector.
function y = colcopyi(v,n) % COLCOPYI y = colcopyi(v,n) n columns in reverse order % Version of 8/22/96 % v a row or column vector. % Treats v as column vector, % reverses the order of the % elements, and makes n copies. % Procedure based on "Tony's trick" N = ones(1,n); [r,c] = size(v); if r == 1 v = v(c:-1:1)'; else v = v(r:-1:1); end y = v(:,N);
rowcopy.mfunction y = rowcopy(v,n) treats row or column vector
v as a row vector and makes a matrix with n rows of v.
function y = rowcopy(v,n) % ROWCOPY y = rowcopy(v,n) n rows of v % Version of 5/7/96 % v a row or column vector % Treats v as row vector % and makes n copies % Procedure based on "Tony's trick" [r,c] = size(v); if c == 1 v = v'; end y = v(ones(1,n),:);
repseq.mfunction y = repseq(V,n) replicates vector V n
times—horizontally if V is a row vector and vertically if V is a column vector.
function y = repseq(V,n); % REPSEQ y = repseq(V,n) Replicates vector V n times % Version of 3/27/97 % n replications of vector V % Horizontally if V a row vector % Vertically if V a column vector m = length(V); s = rem(0:n*m-1,m)+1; y = V(s);
total.m Total of all elements in a matrix, calculated by:
total(x) = sum(sum(x)).
function y = total(x) % TOTAL y = total(x) % Version of 8/1/93 % Total of all elements in matrix x. y = sum(sum(x));
dispv.m Matrices A,B are transposed and displayed side by side.
function y = dispv(A,B) % DISPV y = dispv(A,B) Transpose of A, B side by side % Version of 5/3/96 % A, B are matrices of the same size % They are transposed and displayed % side by side. y = [A;B]';
roundn.mfunction y = roundn(A,n) rounds matrix A to n
decimal places.
function y = roundn(A,n); % ROUNDN y = roundn(A,n) % Version of 7/28/97 % Rounds matrix A to n decimals y = round(A*10^n)/10^n;
arrep.mfunction y = arrep(n,k) forms all arrangements, with
repetition, of k elements from the sequence 1:n.
function y = arrep(n,k); % ARREP y = arrep(n,k); % Version of 7/28/97 % Computes all arrangements of k elements of 1:n, % with repetition allowed. k may be greater than n. % If only one input argument n, then k = n. % To get arrangements of column vector V, use % V(arrep(length(V),k)). N = 1:n; if nargin == 1 k = n; end y = zeros(k,n^k); for i = 1:k y(i,:) = rep(elrep(N,1,n^(k-i)),1,n^(i-1)); end
The analysis of logical combinations of events (as sets) is systematized by the use of the minterm expansion. This leads naturally to the notion of minterm vectors. These are zero-one vectors which can be combined by logical operations. Production of the basic minterm patterns is essential to a number of operations. The following m-programs are key elements of various other programs.
minterm.mfunction y = minterm(n,k) generates the kth minterm
vector in a class of n.
function y = minterm(n,k) % MINTERM y = minterm(n,k) kth minterm of class of n % Version of 5/5/96 % Generates the kth minterm vector in a class of n % Uses m-function rep y = rep([zeros(1,2^(n-k)) ones(1,2^(n-k))],1,2^(k-1));
mintable.mfunction y = mintable(n) generates a table of minterm
vectors by repeated use of the m-function minterm.
function y = mintable(n)
% MINTABLE y = mintable(n) Table of minterms vectors
% Version of 3/2/93
% Generates a table of minterm vectors
% Uses the m-function minterm
y = zeros(n,2^n);
for i = 1:n
y(i,:) = minterm(n,i);
end
minvec3.m sets basic minterm vectors A,B,C,Ac,Bc,Cc for the class {A,B,C}. (Similarly for minvec4.m, minvec5.m, etc.)
% MINVEC3 file minvec3.m Basic minterm vectors
% Version of 1/31/95
A = minterm(3,1);
B = minterm(3,2);
C = minterm(3,3);
Ac = ~A;
Bc = ~B;
Cc = ~C;
disp('Variables are A, B, C, Ac, Bc, Cc')
disp('They may be renamed, if desired.')
minmapfunction y = minmap(pm) reshapes a row or column vector
pm of minterm probabilities into minterm map format.
function y = minmap(pm)
% MINMAP y = minmap(pm) Reshapes vector of minterm probabilities
% Version of 12/9/93
% Reshapes a row or column vector pm of minterm
% probabilities into minterm map format
m = length(pm);
n = round(log(m)/log(2));
a = fix(n/2);
if m ~= 2^n
disp('The number of minterms is incorrect')
else
y = reshape(pm,2^a,2^(n-a));
end
binary.mfunction y = binary(d,n) converts a matrix d of
floating point nonnegative integers to a matrix of binary equivalents, one on each row.
Adapted from m-functions written by Hans Olsson and by Simon Cooke. Each matrix row may
be converted to an unspaced string of zeros and ones by the device ys = setstr(y + '0').
function y = binary(d,n) % BINARY y = binary(d,n) Integers to binary equivalents % Version of 7/14/95 % Converts a matrix d of floating point, nonnegative % integers to a matrix of binary equivalents. Each row % is the binary equivalent (n places) of one number. % Adapted from the programs dec2bin.m, which shared % first prize in an April 95 Mathworks contest. % Winning authors: Hans Olsson from Lund, Sweden, % and Simon Cooke from Glasgow, UK. % Each matrix row may be converted to an unspaced string % of zeros and ones by the device: ys = setstr(y + '0'). if nargin < 2, n = 1; end % Allows omission of argument n [f,e] = log2(d); n = max(max(max(e)),n); y = rem(floor(d(:)*pow2(1-n:0)),2);
mincalc.m The m-procedure mincalc determines minterm probabilities from suitable data. For a discussion of the data formatting and certain problems, see 2.6.
% MINCALC file mincalc.m Determines minterm probabilities
% Version of 1/22/94 Updated for version 5.1 on 6/6/97
% Assumes a data file which includes
% 1. Call for minvecq to set q basic minterm vectors, each (1 x 2^q)
% 2. Data vectors DV = matrix of md data Boolean combinations of basic sets--
% Matlab produces md minterm vectors-- one on each row.
% The first combination is always A|Ac (the whole space)
% 3. DP = row matrix of md data probabilities.
% The first probability is always 1.
% 4. Target vectors TV = matrix of mt target Boolean combinations.
% Matlab produces a row minterm vector for each target combination.
% If there are no target combinations, set TV = [];
[md,nd] = size(DV);
ND = 0:nd-1;
ID = eye(nd); % Row i is minterm vector i-1
[mt,nt] = size(TV);
MT = 1:mt;
rd = rank(DV);
if rd < md
disp('Data vectors are NOT linearly independent')
else
disp('Data vectors are linearly independent')
end
% Identification of which minterm probabilities can be determined from the data
% (i.e., which minterm vectors are not linearly independent of data vectors)
AM = zeros(1,nd);
for i = 1:nd
AM(i) = rd == rank([DV;ID(i,:)]); % Checks for linear dependence of each
end
am = find(AM); % minterm vector
CAM = ID(am,:)/DV; % Determination of coefficients for the available minterms
pma = DP*CAM'; % Calculation of probabilities of available minterms
PMA = [ND(am);pma]';
if sum(pma < -0.001) > 0 % Check for data consistency
disp('Data probabilities are INCONSISTENT')
else
% Identification of which target probabilities are computable from the data
CT = zeros(1,mt);
for j = 1:mt
CT(j) = rd == rank([DV;TV(j,:)]);
end
ct = find(CT);
CCT = TV(ct,:)/DV; % Determination of coefficients for computable targets
ctp = DP*CCT'; % Determination of probabilities
disp(' Computable target probabilities')
disp([MT(ct); ctp]')
end % end for "if sum(pma < -0.001) > 0"
disp(['The number of minterms is ',num2str(nd),])
disp(['The number of available minterms is ',num2str(length(pma)),])
disp('Available minterm probabilities are in vector pma')
disp('To view available minterm probabilities, call for PMA')
mincalct.m Modification of mincalc. Assumes mincalc has been run, calls for new target vectors and performs same calculations as mincalc.
% MINCALCT file mincalct.m Aditional target probabilities
% Version of 9/1/93 Updated for version 5 on 6/6/97
% Assumes a data file which includes
% 1. Call for minvecq to set q basic minterm vectors.
% 2. Data vectors DV. The first combination is always A|Ac.
% 3. Row matrix DP of data probabilities. The first entry is always 1.
TV = input('Enter matrix of target Boolean combinations ');
[md,nd] = size(DV);
[mt,nt] = size(TV);
MT = 1:mt;
rd = rank(DV);
CT = zeros(1,mt); % Identification of computable target probabilities
for j = 1:mt
CT(j) = rd == rank([DV;TV(j,:)]);
end
ct = find(CT);
CCT = TV(ct,:)/DV; % Determin