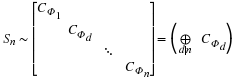
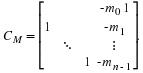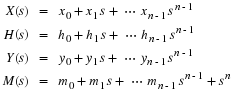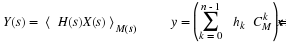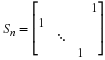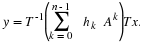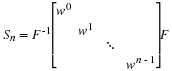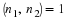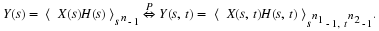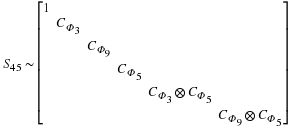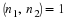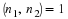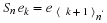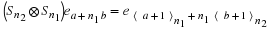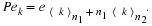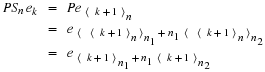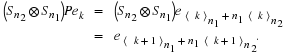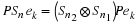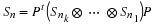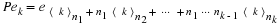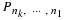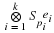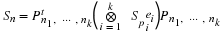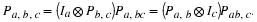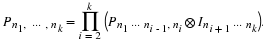Because we compute prime point DFTs by converting them in to
circular convolutions, most of this and the next section is devoted
to an explanation of the split nesting convolution algorithm.
In this section we introduce the various operations needed
to carry out the split nesting algorithm.
In particular, we describe the prime factor permutation
that is used to convert a one-dimensional circular convolution
into a multi-dimensional one.
We also discuss the reduction operations needed when
the Chinese Remainder Theorem for polynomials is used
in the computation of convolution.
The reduction operations needed for the split nesting algorithm
are particularly well organized.
We give an explicit matrix description of the reduction operations
and give a program that implements the action of these
reduction operations.
The presentation relies upon the notions of similarity
transformations, companion matrices and Kronecker products.
With them, we describe the split nesting algorithm in a manner
that brings out its structure.
We find that when companion matrices are used to describe
convolution, the reduction operations block diagonalizes
the circular shift matrix.
The companion matrix
of a monic polynomial,
M(s)=m0+m1s+⋯+mn–1sn–1+sn
is given by
Its usefulness in the following discussion comes from
the following relation which permits a matrix formulation
of convolution.
Let
Then
where  ,
,
 ,
and CM is the companion matrix of M(s).
In Equation 2.3, we say y is the convolution of x and
h with respect to M(s).
In the case of circular convolution,
M(s)=sn–1 and Csn–1 is
the circular shift matrix
denoted by Sn,
,
and CM is the companion matrix of M(s).
In Equation 2.3, we say y is the convolution of x and
h with respect to M(s).
In the case of circular convolution,
M(s)=sn–1 and Csn–1 is
the circular shift matrix
denoted by Sn,
Notice that any circulant matrix can be written as
∑khkSkn.
Similarity transformations
can be used to interpret the action of some convolution algorithms.
If CM=T–1AT for some matrix T
(CM and A are similar, denoted
CM∼A),
then Equation 2.3 becomes
That is, by employing the similarity transformation given
by T in this way, the action of Skn is
replaced by that of Ak.
Many circular convolution algorithms can be understood,
in part,
by understanding the manipulations made to Sn
and the resulting new matrix A.
If the transformation T is to be useful,
it must satisfy two requirements:
(1) Tx must be simple to compute, and
(2) A must have some advantageous structure.
For example, by the convolution property of the DFT,
the DFT matrix F diagonalizes Sn,
so that it diagonalizes every circulant matrix.
In this case, Tx can be computed by using an FFT and
the structure of A is the simplest possible.
So the two above mentioned conditions are met.
The Winograd Structure
can be described in this manner also.
Suppose M(s) can be factored as M(s)=M1(s)M2(s)
where M1 and M2 have no common roots,
then CM∼(CM1 ⊕ CM2)
where ⊕ denotes the matrix direct sum.
Using this similarity and recalling Equation 2.3,
the original convolution is decomposed into
disjoint convolutions.
This is, in fact, a statement of the Chinese Remainder Theorem
for polynomials expressed in matrix notation.
In the case of circular convolution,
sn–1=∏d|nΦd(s), so that
Sn can be transformed to a block diagonal matrix,
where Φd(s) is the dth cyclotomic polynomial.
In this case, each block represents a convolution
with respect to a cyclotomic polynomial, or a
`cyclotomic convolution'.
Winograd's approach carries out these cyclotomic convolutions
using the Toom-Cook algorithm.
Note that for each divisor, d, of n there is a
corresponding block on the diagonal of size
φ(d),
for the degree of Φd(s)
is φ(d)
where φ(·) is the Euler totient function.
This method is good for short lengths, but
as n increases
the cyclotomic convolutions become cumbersome,
for as the number of distinct prime divisors of d
increases,
the operation described by ∑khk(CΦd)k
becomes more difficult to implement.
The Agarwal-Cooley Algorithm
utilizes the fact that
(2.8)
Sn
=
Pt
(Sn1 ⊗ Sn2)
P
where n=n1n2, 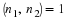 and
P is an appropriate permutation 1.
This converts the one dimensional circular convolution
of length n to a two dimensional one of length
n1 along one dimension and length n2 along
the second.
Then an n1-point and an n2-point circular convolution
algorithm can be combined to obtain an n-point algorithm.
In polynomial notation, the mapping accomplished by
this permutation
P can be informally indicated by
and
P is an appropriate permutation 1.
This converts the one dimensional circular convolution
of length n to a two dimensional one of length
n1 along one dimension and length n2 along
the second.
Then an n1-point and an n2-point circular convolution
algorithm can be combined to obtain an n-point algorithm.
In polynomial notation, the mapping accomplished by
this permutation
P can be informally indicated by
It should be noted that Equation 2.8
implies that a circulant matrix of size n1n2 can be
written as a block circulant matrix with circulant
blocks.
The Split-Nesting algorithm
3 combines the structures of the
Winograd and Agarwal-Cooley methods, so that Sn is transformed
to a block diagonal
matrix as in Equation 2.7,
Here
Ψ(d)=⊗p|d,p∈PCΦHd(p)
where Hd(p) is the highest power of p dividing d, and
P is the set of primes.
In this structure a multidimensional cyclotomic convolution,
represented by Ψ(d), replaces each cyclotomic convolution
in Winograd's algorithm (represented by CΦd in
Equation 2.7.
Indeed, if the product of b1,⋯,bk is d and they are
pairwise relatively prime, then
CΦd∼CΦb1⊗⋯⊗CΦbk.
This gives a method for combining cyclotomic convolutions
to compute a longer circular convolution.
It is like the Agarwal-Cooley method but requires fewer
additions 3.
Prime Factor Permutations
One can obtain Sn1⊗Sn2 from
Sn1n2 when 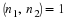 ,
for in this case,
Sn is similar to Sn1⊗Sn2, n=n1n2.
Moreover, they are related by a permutation.
This permutation is that of the prime factor FFT
algorithms and is employed in nesting algorithms
for circular convolution 1, 2.
The permutation is described by Zalcstein 7,
among others, and it is his description we draw on in the following.
,
for in this case,
Sn is similar to Sn1⊗Sn2, n=n1n2.
Moreover, they are related by a permutation.
This permutation is that of the prime factor FFT
algorithms and is employed in nesting algorithms
for circular convolution 1, 2.
The permutation is described by Zalcstein 7,
among others, and it is his description we draw on in the following.
Let n=n1n2 where 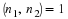 .
Define ek, (0≤k≤n–1), to be the standard basis vector,
(0,⋯,0,1,0,⋯,0)t, where the 1 is in
the kth position.
Then, the circular shift matrix, Sn, can be described by
.
Define ek, (0≤k≤n–1), to be the standard basis vector,
(0,⋯,0,1,0,⋯,0)t, where the 1 is in
the kth position.
Then, the circular shift matrix, Sn, can be described by
Note that, by inspection,
where 0≤a≤n1–1 and 0≤b≤n2–1.
Because n1 and n2 are relatively prime a permutation matrix P
can be defined by
With this P,
and
Since 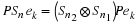 and P–1=Pt, one gets, in the multi-factor case, the following.
and P–1=Pt, one gets, in the multi-factor case, the following.
Lemma
If n=n1⋯nk and n1,...,nk are pairwise
relatively prime, then
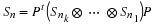 where P is the permutation matrix given by
where P is the permutation matrix given by
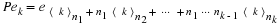 .
.
This useful permutation will be denoted here as
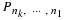 .
If n=p1e1p2e2⋯pkek then
this permutation yields the matrix, Sp1e1⊗⋯⊗Spkek. This product can be written
simply as
.
If n=p1e1p2e2⋯pkek then
this permutation yields the matrix, Sp1e1⊗⋯⊗Spkek. This product can be written
simply as 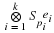 , so that
one has
, so that
one has
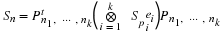 .
.
It is quite simple to show that
In general, one has
A Matlab function for Pa,b⊗Is is
pfp2I()
in one of the appendices.
This program is a direct implementation
of the definition.
In a paper by Templeton 5, another method for
implementing Pa,b, without `if' statements,
is given. That method requires some precalculations, however.
A function for
Pn1,⋯,nk is
pfp(). It uses Equation 2.18