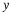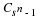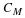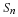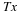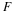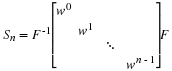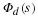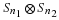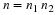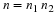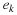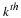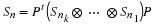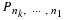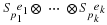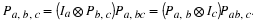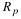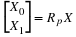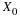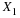A basic technique in fast algorithms for convolution is that of interpolation. That is, two polynomials are evaluated at some common points and these values are multiplied 1, 3, 4. By interpolating these products, the product of the two original polynomials can be determined. In the Winograd short convolution algorithms, this technique is used and the common points of evaluation are the simple integers, 0, 1, and –1. Indeed, the computational savings of the interpolation technique depends on the use of special points at which to interpolate. In the Winograd algorithm the computational savings come from the simplicity of the small integers. (As an algorithm for convolution, the FFT interpolates over the roots of unity.) This interpolation method is often called the Toom-Cook method and it is given by two matrices that describe a bilinear form.
We use bilinear forms to give a matrix formulation of the split nesting algorithm. The split nesting algorithm combines smaller convolution algorithms to obtain algorithms for longer lengths. We use the Kronecker product to explicitly describe the way in which smaller convolution algorithms are appropriately combined.
First we consider the linear convolution of two n point sequences. Recall that the linear convolution of h and x can be represented by a matrix vector product. When n=3:
This linear convolution matrix can be written as h0H0+h1H1+h2H2 where Hk are clear.
The product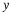 
can be found using the Toom-Cook algorithm, an
interpolation method.
Choose 2n–1 interpolation points, i1,⋯,i2n–1,
and let A and C be matrices given by
That is, A is a degree n–1 Vandermonde matrix and C is the inverse of the degree 2n–2 Vandermonde matrix specified by the same points specifying A. With these matrices, one has
where * denotes point by point multiplication.
The terms Ah and Ax are the values of
H(s) and X(s) at the points i1,⋯i2n–1.
The point by point multiplication gives the
values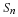 
.
The operation of C obtains the coefficients of
Y(s) from its values at these points of evaluation.
This is the bilinear form
and it implies that
If n=2, then equations Equation 3.3 and Equation 3.4 give
When the interpolation points are 0, 1,and –1,
However, A and C do not need to be Vandermonde
matrices as in Equation 3.2.
For example, see the two point linear convolution algorithm
in the appendix.
As long as A and C are matrices such that
, then the linear convolution
of x and h is given by
the bilinear form y=C{Ah*Ax}.
More generally, as long as A, B and C are
matrices satisfying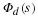 
,
then y=C{Bh*Ax} computes the
linear convolution of h and x.
For convenience, if C{Ah*Ax}
computes the n point linear convolution of h and x
(both h and x are n point sequences),
then we say “(A,B,C) describes a bilinear
form for n point linear convolution."
Similarly, we can write a bilinear form for cyclotomic
convolution.
Let d be any positive integer and let X(s)
and H(s) be polynomials of degree
φ(d)–1 where φ(·) is the Euler
totient function.
If A, B and C are matrices
satisfying 
for 0≤k≤φ(d)–1,
then the coefficients of Y(s)=〈X(s)H(s)〉Φd(s)
are given by y=C{Bh*Ax}.
As above, if y=C{Bh*Ax} computes the
d-cyclotomic convolution, then we say
“(A,B,C) describes a bilinear form for Φd(s)
convolution."
But since 〈X(s)H(s)〉Φd(s) can be found by computing the product of X(s) and H(s) and reducing the result, a cyclotomic convolution algorithm can always be derived by following a linear convolution algorithm by the appropriate reduction operation: If G is the appropriate reduction matrix and if (A,B,F) describes a bilinear form for a φ(d) point linear convolution, then (A,B,GF) describes a bilinear form for Φd(s) convolution. That is, y=GF{Bh*Ax} computes the coefficients of 〈X(s)H(s)〉Φd(s).
By using the Chinese Remainder Theorem for polynomials, circular convolution can be decomposed into disjoint cyclotomic convolutions. Let p be a prime and consider p point circular convolution. Above we found that
and therefore
If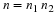 
describes a bilinear form for Φp(s)
convolution,
then
and consequently the circular convolution of h and x can be computed by
where A=1⊕Ap, B=1⊕Bp and C=1⊕Cp. We say (A,B,C) describes a bilinear form for p point circular convolution. Note that if (D,E,F) describes a (p–1) point linear convolution then Ap, Bp and Cp can be taken to be Ap=D, Bp=E and Cp=GpF where Gp represents the appropriate reduction operations. Specifically, Gp is given by Equation 42 from Preliminaries.
Next we consider pe point circular convolution.
Recall that
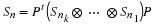as in Equation 27 from Preliminaries
so that the circular convolution is decomposed into
a set of e+1 disjoint Φpi(s) convolutions.
If 
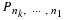describes a bilinear form for Φpi(s) convolution
and if
then 
describes a bilinear form for pe point circular convolution.
In particular, if
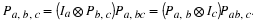describes a bilinear form for d point
linear convolution, then Api, Bpi and Cpi
can be taken to be
where Gpi represents the appropriate reduction operation and φ(·) is the Euler totient function. Specifically, Gpi has the following form
if p≥3, while
Note that the matrix Rpe block diagonalizes Spe and each diagonal block represents a cyclotomic convolution. Correspondingly, the matrices A, B and C of the bilinear form also have a block diagonal structure.
We now describe the split-nesting algorithm for general length circular convolution 4. Let n=p1e1⋯pkek where pi are distinct primes. We have seen that
where P is the prime factor permutation
P=Pp1e1,⋯,pkek
and R represents the reduction operations.
For example, see Equation 46 in Preliminaries.
RP block diagonalizes Sn and each diagonal
block represents a multi-dimensional cyclotomic
convolution.
To obtain a bilinear form for a multi-dimensional convolution,
we can combine bilinear forms for one-dimensional
convolutions.
If 
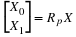describes a bilinear form for Φpji(s)
convolution
and if
with
where Hd(p) is the highest power of p dividing