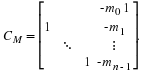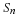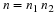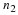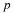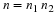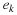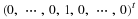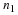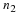Implementing Kronecker Products Efficiently
In the algorithm described above
we encountered expressions
of the form A1⊗A2⊗⋯⊗An
which we denote by
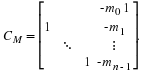 To calculate the product (⊗iAi)x
it is computationally advantageous to factor
⊗iAi into terms of the form
I⊗Ai⊗I1.
Then each term represents a set of copies of Ai.
First, recall the following property of Kronecker products
To calculate the product (⊗iAi)x
it is computationally advantageous to factor
⊗iAi into terms of the form
I⊗Ai⊗I1.
Then each term represents a set of copies of Ai.
First, recall the following property of Kronecker products
(5.1)
A
B
⊗
C
D
=
(
A
⊗
C
)
(
B
⊗
D
)
.
This property can be used to factor ⊗iAi
in the following way.
Let the number of rows and columns of Ai be denoted
by ri and ci respectively.
Then
But we can also write
Note that in factorization Equation 5.2, copies of
A2 are applied to the data vector x first,
followed by copies of A1.
On the other hand, in factorization Equation 5.3, copies of
A1 are applied to the data vector x first,
followed by copies of A2.
These two factorizations can be distinguished by the
sequence in which A1 and A2 are ordered.
Lets compare the computational complexity of
factorizations
Equation 5.2 and Equation 5.3.
Notice that Equation 5.2 consists of r2 copies of
A1 and c1 copies of A2,
therefore
Equation 5.2 has a computational cost of
r2Q1+c1Q2 where
Qi is the computational cost of Ai.
On the other hand,
the computational cost of Equation 5.3 is
c2Q1+r1Q2.
That is, the factorizations Equation 5.2
and Equation 5.3 have in general different
computational costs
when Ai are not square.
Further, observe that Equation 5.2 is the more
efficient factorization exactly when
(5.4)
r2
Q1
+
c1
Q2
<
c2
Q1
+
r1
Q2
or equivalently, when
Consequently,
in the more efficient factorization,
the operation Ai applied to the data vector x first is the one
for which the ratio 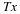 is the
more negative.
If r1>c1 and r2<c2
then Equation 5.4 is always true (Qi is always positive).
Therefore, in the most computationally efficient
factorization of A1⊗A2, matrices with fewer rows than
columns are always applied to the data vector x before
matrices with more rows than columns.
If both matrices are square, then their ordering does not
affect the computational efficiency, because
in that case
each ordering has the same computation cost.
is the
more negative.
If r1>c1 and r2<c2
then Equation 5.4 is always true (Qi is always positive).
Therefore, in the most computationally efficient
factorization of A1⊗A2, matrices with fewer rows than
columns are always applied to the data vector x before
matrices with more rows than columns.
If both matrices are square, then their ordering does not
affect the computational efficiency, because
in that case
each ordering has the same computation cost.
We now consider the Kronecker product of more than two matrices.
For the Kronecker product ⊗ni=1Ai there
are n! possible different ways in which to order
the operations Ai.
For example
Each factorization of ⊗iAi can be described by
a permutation g(·) of {1,...,n} which gives
the order in which Ai is applied to the data vector x.
Ag(1) is the first operation applied to the
data vector x, Ag(2) is the second, and so on.
For example, the factorization Equation 5.6 is described
by the permutation g(1)=3, g(2)=1, g(3)=2.
For n=3,
the computational cost of each factorization can be written
as
(5.7)
C
(
g
)
=
Qg
(
1
)
cg
(
2
)
cg
(
3
)
+
rg
(
1
)
Qg
(
2
)
cg
(
3
)
+
rg
(
1
)
rg
(
2
)
Qg
(
3
)
In general
Therefore, the most efficient factorization of ⊗iAi
is described by the permutation g(·) that minimizes C.
It turns out that for the Kronecker product of more than two
matrices, the ordering of operations that describes
the most efficient factorization of ⊗iAi
also depends only on the ratios 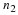 .
To show that this is the case, suppose
u(·) is the permutation that
minimizes C,
then u(·) has the property that
.
To show that this is the case, suppose
u(·) is the permutation that
minimizes C,
then u(·) has the property that
for k=1,⋯,n–1.
To support this, note that since u(·)
is the permutation that minimizes C,
we have in particular
(5.10)
C
(
u
)
≤
C
(
v
)
where v(·) is
the permutation defined by the following:
Because only two terms in Equation 5.8 are different,
we have from Equation 5.10
which, after canceling common terms from each side, gives
(5.13)
Qu
(
k
)
cu
(
k
+
1
)
+
ru
(
k
)
Qu
(
k
+
1
)
≤
Qv
(
k
)
cv
(
k
+
1
)
+
rv
(
k
)
Qv
(
k
+
1
)
.
Since v(k)=u(k+1) and v(k+1)=u(k)
this becomes
(5.14)
Qu
(
k
)
cu
(
k
+
1
)
+
ru
(
k
)
Qu
(
k
+
1
)
≤
Qu
(
k
+
1
)
cu
(
k
)
+
ru
(
k
+
1
)
Qu
(
k
)
which is equivalent to Equation 5.9.
Therefore, to find the best factorization of ⊗iAi
it is necessary only to compute the ratios
 and to order them in an non-decreasing order.
The operation Ai whose index appears first in this list
is applied to the data vector x first, and so on
and to order them in an non-decreasing order.
The operation Ai whose index appears first in this list
is applied to the data vector x first, and so on
As above, if ru(k+1)>cu(k+1) and ru(k)<cu(k)
then Equation 5.14 is always true.
Therefore, in the most computationally efficient
factorization of ⊗iAi, all matrices with fewer rows than columns are
always applied to the data vector x before
any matrices with more rows than columns.
If some matrices are square, then their ordering does not
affect the computational efficiency as long
as they are applied after all matrices
with fewer rows than columns and before
all matrices with more rows than columns.
Once the permutation g(·) that minimizes C
is determined by ordering the ratios
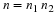 ,
⊗iAi can be written as
,
⊗iAi can be written as
where
and where γ(·) is defined by
A Matlab program that computes the permutation
that describes the computationally most efficient
factorization of ⊗ni=1Ai is cgc()
.
It also gives the resulting computational cost.
It requires the computational cost of each of the
matrices Ai and the number of rows and columns
of each.
function [g,C] = cgc(Q,r,c,n)
% [g,C] = cgc(Q,r,c,n);
% Compute g and C
% g : permutation that minimizes C
% C : computational cost of Kronecker product of A(1),...,A(n)
% Q : computation cost of A(i)
% r : rows of A(i)
% c : columns of A(i)
% n : number of terms
f = find(Q==0);
Q(f) = eps * ones(size(Q(f)));
Q = Q(:);
r = r(:);
c = c(:);
[s,g] = sort((r-c)./Q);
C = 0;
for i = 1:n
C = C + prod(r(g(1:i-1)))*Q(g(i))*prod(c(g(i+1:n)));
end
C = round(C);
The Matlab program kpi()
implements the Kronecker
product ⊗ni=1Ai.
function y = kpi(d,g,r,c,n,x)
% y = kpi(d,g,r,c,n,x);
% Kronecker Product : A(d(1)) kron ... kron A(d(n))
% g : permutation of 1,...,n
% r : [r(1),...,r(n)]
% c : [c(1),..,c(n)]
% r(i) : rows of A(d(i))
% c(i) : columns of A(d(i))
% n : number of terms
for i = 1:n
a = 1;
for k = 1:(g(i)-1)
if i > find(g==k)
a = a * r(k);
else
a = a * c(k);
end
end
b = 1;
for k = (g(i)+1):n
if i > find(g==k)
b = b * r(k);
else
b = b * c(k);
end
end
% y = (I(a) kron A(d(g(i))) kron I(b)) * x;
y = IAI(d(g(i)),a,b,x);
end
where the last line of code
calls a function that implements 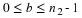 .
That is, the program
.
That is, the program IAI(i,a,b,x)
implements
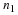 .
.
The Matlab program IAI
implements 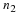
function y = IAI(A,r,c,m,n,x)
% y = (I(m) kron A kron I(n))x
% r : number of rows of A
% c : number of columns of A
v = 0:n:n*(r-1);
u = 0:n:n*(c-1);
for i = 0:m-1
for j = 0:n-1
y(v+i*r*n+j+1) = A * x(u+i*c*n+j+1);
end
end
It simply uses two loops to implement the mn copies
of A. Each copy of A is applied to a different
subset of the elements of x.
Vector/Parallel Interpretation
The command I⊗A⊗I where ⊗ is the
Kronecker (or Tensor) product can be interpreted as a
vector/parallel command 2, 3.
In these references, the implementation of these
commands is discussed in detail and
they have found that the Ten