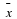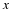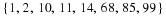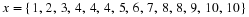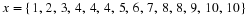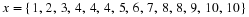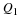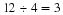Geometry (Greek: geo = earth, metria = measure) arose as the field of knowledge dealing with spatial relationships. It was one of the two fields of pre-modern mathematics, the other being the study of numbers. In modern times, geometric concepts have become very complex and abstract and are barely recognizable as the descendants of early geometry. Geometry is often split into Euclidean geometry and analytical geometry. Euclidean geometry is covered in this chapter.

In this section we will look at the properties of some special quadrilaterals. We will then use these properties to solve geometrical problems. It should be noted that although all the properties of a figure are given, we only need one unique property of the quadrilateral to prove that it is that quadrilateral. For example, if we have a quadrilateral with two pairs of opposite sides parallel, then that quadrilateral is a parallelogram. We can then prove the other properties of the quadrilateral using what we have learnt about parallel lines and triangles.

Trapezium

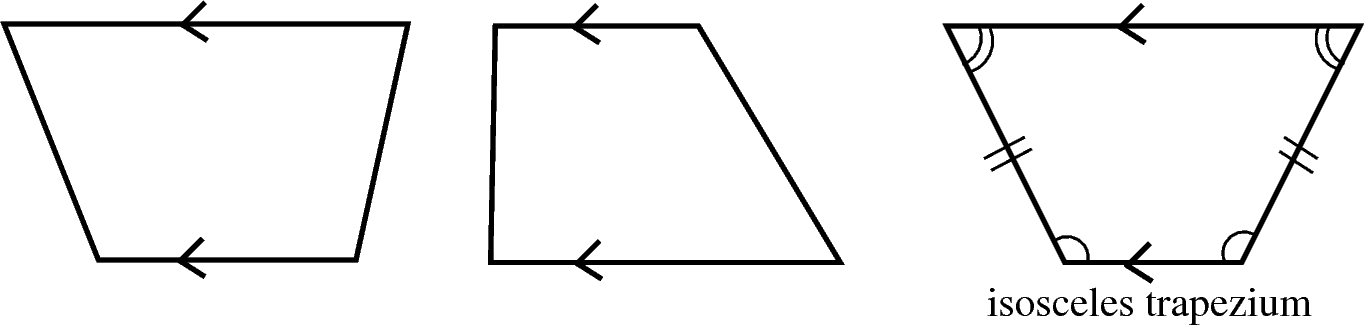
A trapezium is a quadrilateral with one pair of parallel opposite sides. It may also be called a trapezoid. A special type of trapezium is the isosceles trapezium, where one pair of opposite sides is parallel, the other pair of sides is equal in length and the angles at the ends of each parallel side are equal. An isosceles trapezium has one line of symmetry and its diagonals are equal in length.

Note: The term trapezoid is predominantly used in North America and refers to what we call a trapezium. Rather confusingly, they use the term 'trapezium' to refer to a general irregular quadrilateral, that is a quadrilateral with no parallel sides!

Figure 14.1. 

Examples of trapeziums.

Parallelogram

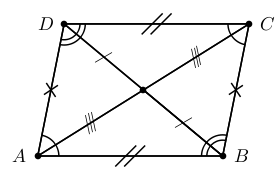
A trapezium with both sets of opposite sides parallel is called a parallelogram. A summary of the properties of a parallelogram is:

• Both pairs of opposite sides are parallel.

• Both pairs of opposite sides are equal in length.

• Both pairs of opposite angles are equal.

• Both diagonals bisect each other (i.e. they cut each other in half).

Figure 14.2. 

An example of a parallelogram.

Rectangle

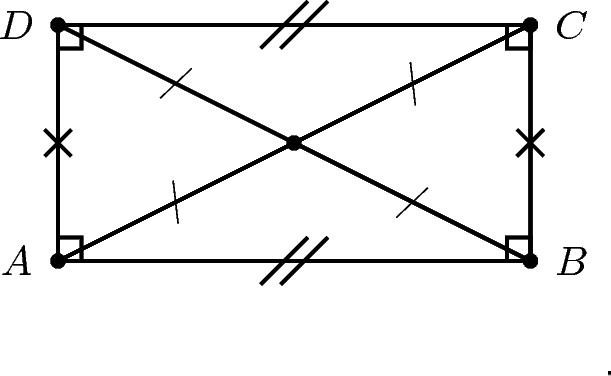
A rectangle is a parallelogram that has all four angles equal to 90^∘. A summary of the properties of a rectangle is:

• Both pairs of opposite sides are parallel.

• Both pairs of opposite sides are of equal length.

• Both diagonals bisect each other.

• Diagonals are equal in length.

• All angles at the corners are right angles.

Figure 14.3. 

Example of a rectangle.

Rhombus

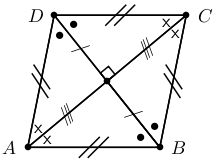
A rhombus is a parallelogram that has all four sides of equal length. A summary of the properties of a rhombus is:

• Both pairs of opposite sides are parallel.

• All sides are equal in length.

• Both pairs of opposite angles are equal.

• Both diagonals bisect each other at 90^∘.

• Diagonals of a rhombus bisect both pairs of opposite angles.

Figure 14.4. 

An example of a rhombus. A rhombus is a parallelogram with all sides equal.

Square

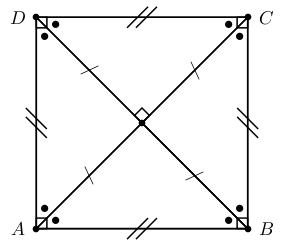
A square is a rhombus that has all four angles equal to 90^∘.

A summary of the properties of a square is:

• Both pairs of opposite sides are parallel.

• All sides are equal in length.

• All angles are equal to 90^∘.

• Both pairs of opposite angles are equal.

• Both diagonals bisect each other at 90^∘.

• Diagonals are equal in length.

• Diagonals bisect both pairs of opposite angles (ie. all 45^∘).

Figure 14.5. 

An example of a square. A square is a rhombus with all angles equal to 90^∘.

Kite

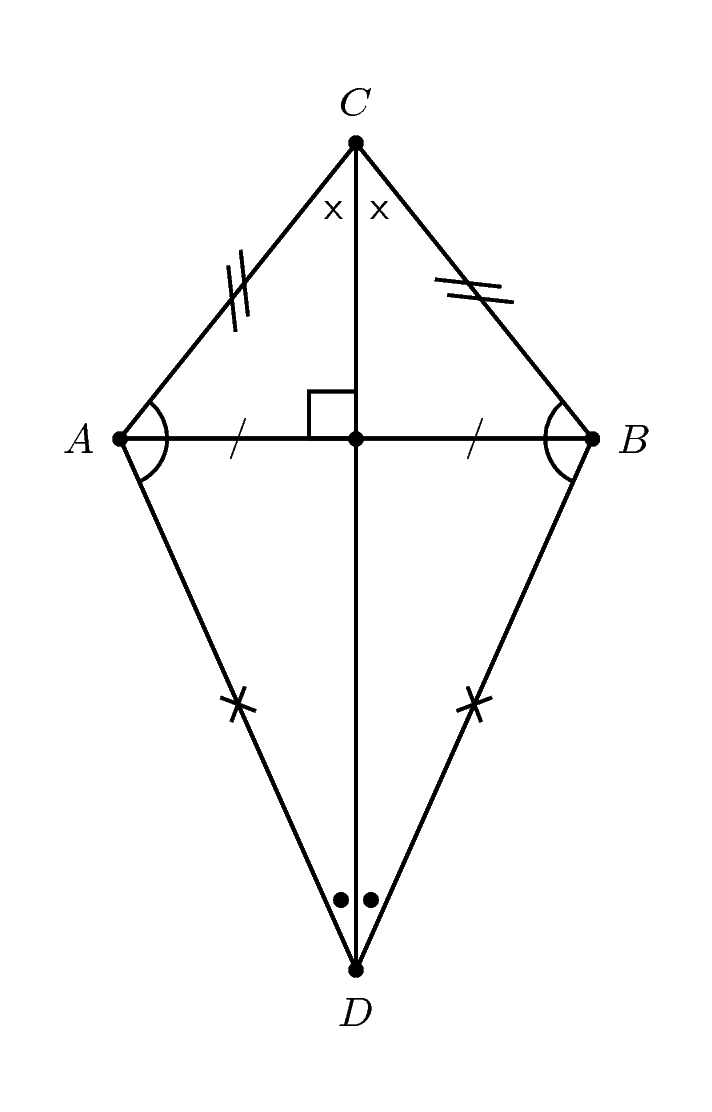
A kite is a quadrilateral with two pairs of adjacent sides equal.

A summary of the properties of a kite is:

• Two pairs of adjacent sides are equal in length.

• One pair of opposite angles are equal where the angles are between unequal sides.

• One diagonal bisects the other diagonal and one diagonal bisects one pair of opposite angles.

• Diagonals intersect at right-angles.

Figure 14.6. 

An example of a kite.

Rectangles are a special case (or a subset) of parallelograms. Rectangles are parallelograms that have all angles equal to 90. Squares are a special case (or subset) of rectangles. Squares are rectangles that have all sides equal in length. So all squares are parallelograms and rectangles. So if you are asked to prove that a quadrilateral is a parallelogram, it is enough to show that both pairs of opposite sides are parallel. But if you are asked to prove that a quadrilateral is a square, then you must also show that the angles are all right angles and the sides are equal in length.

Polygons are all around us. A stop sign is in the shape of an octagon, an eight-sided polygon. The honeycomb of a beehive consists of hexagonal cells. The top of a desk is a rectangle. Note that although in the first two of these cases the sides of the polygon are all the same, but this need not be the case. Polygons with all sides and angles the same are called 'regular', while those with some sides or angles that are different are called 'irregular'. Although we often work with irregular triangles and quadrilaterals, once one gets up to polygons with greater than four sides, the more interesting ones are often the regular ones.

In this section, you will learn about similar polygons.

Similarity of Polygons

Discussion : Similar Triangles

Fill in the table using the diagram and then answer the questions that follow.

Table 14.1.

=	=...∘	...∘
=	=...∘	=...∘
=	...∘	=...∘

Figure 14.7. 

1. What can you say about the numbers you calculated for: , , ?

2. What can you say about and ?

3. What can you say about and ?

4. What can you say about and ?

If two polygons are similar, one is an enlargement of the other. This means that the two polygons will have the same angles and their sides will be in the same proportion.

We use the symbol ||| to mean is similar to.

Definition: Similar Polygons

Two polygons are similar if:

1. their corresponding angles are equal, and

2. the ratios of corresponding sides are equal.

Exercise 1.: Similarity of Polygons

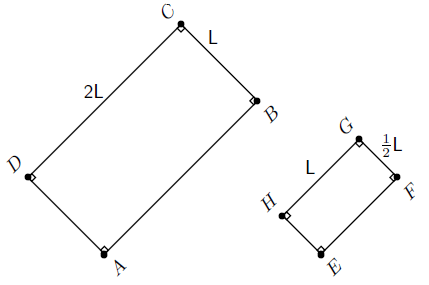
Show that the following two polygons are similar.

Figure 14.7. 

1. Determine what is required :

   We are required to show that the pair of polygons is similar. We can do this by showing that the ratio of corresponding sides is equal and by showing that corresponding angles are equal.

2. Corresponding angles :

   We are given the angles. So, we can show that corresponding angles are equal.

3. Show that corresponding angles are equal :

   All angles are given to be 90^∘ and

   (14.1)

   
4. Show that corresponding sides have equal ratios :

   We first need to see which sides correspond. The rectangles have two equal long sides and two equal short sides. We need to compare the ratio of the long side lengths of the two different rectangles as well as the ratio of the short side lenghts.

   Long sides, large rectangle values over small rectangle values:

   (14.2)

   

   Short sides, large rectangle values over small rectangle values:

   (14.3)

   

   The ratios of the corresponding sides are equal, 2 in this case.

5. Final answer :

   Since corresponding angles are equal and the ratios of the corresponding sides are equal the polygons ABCD and EFGH are similar.

Tip

All squares are similar.

Exercise 2.: Similarity of Polygons

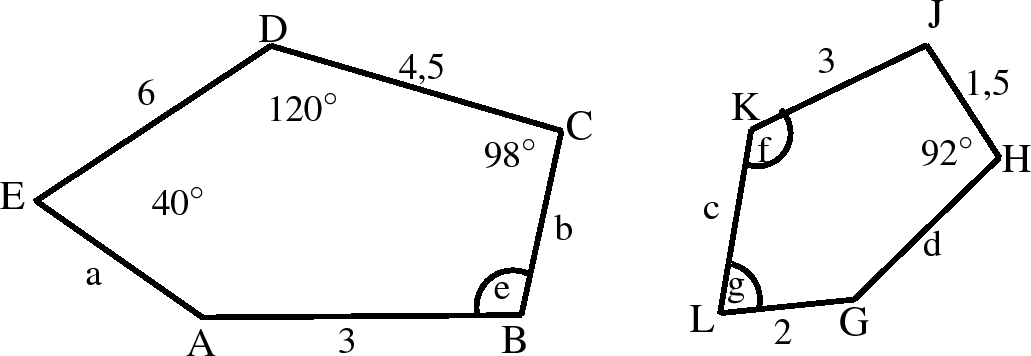
If two pentagons ABCDE and GHJKL are similar, determine the lengths of the sides and angles labelled with letters:

Figure 14.7. 

1. Determine what is given :

   We are given that ABCDE and GHJKL are similar. This means that:

   (14.4)

   

   and

   (14.5)

   
2. Determine what is required :

   We are required to determine the

   1. lengths: a, b, c and d, and

   2. angles: e, f and g.

3. Decide how to approach the problem :

   The corresponding angles are equal, so no calculation is needed. We are given one pair of sides DC and KJ that correspond. so we know that all sides of KJHGL are 1,5 times smaller than ABCDE.

4. Calculate lengths :

   (14.6)

   

5. Calculate angles :

   (14.7)

   

6. Write the final answer :

   (14.8)

   

Activity: Similarity of Equilateral Triangles

Working in pairs, show that all equilateral triangles are similar.

Polygons-mixed

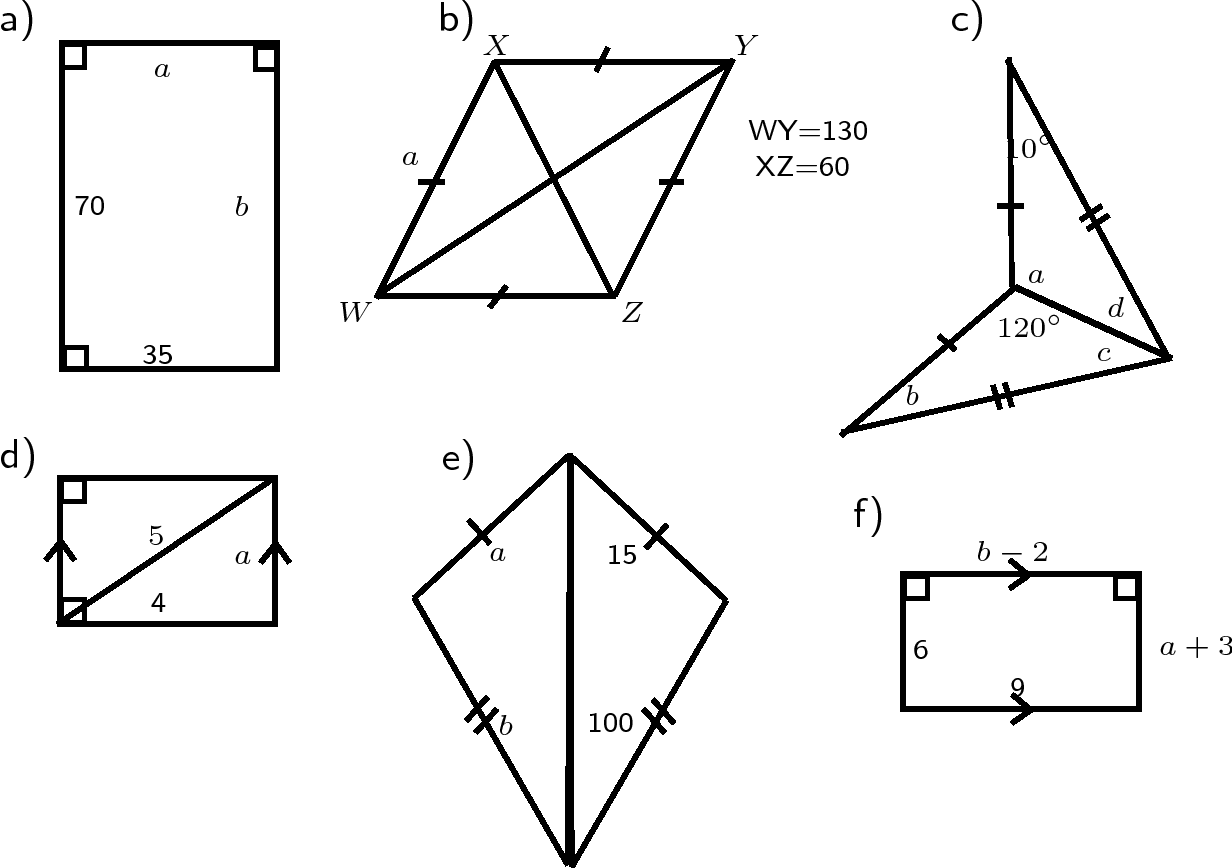
1. Find the values of the unknowns in each case. Give reasons.

   

   Figure 14.8. 

   Click here for the solution

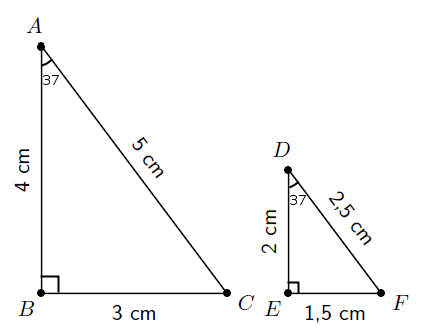
2. Find the angles and lengths marked with letters in the following figures:

   

   Figure 14.9

   Page 1Page 2Page 3Page 4Page 5Page 6Page 7Page 8Page 9Page 10Page 11Page 12Page 13Page 14Page 15Page 16Page 17Page 18Page 19Page 20Page 21Page 22Page 23Page 24

   PREV   NEXT