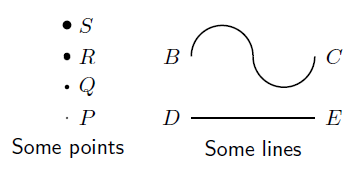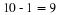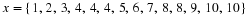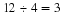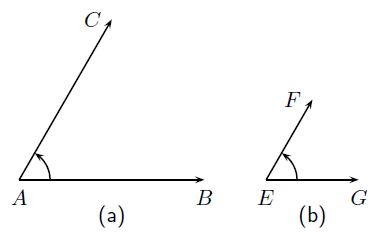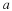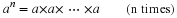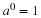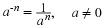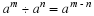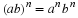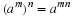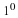The purpose of this chapter is to recap some of the ideas that you learned in geometry and trigonometry in earlier grades. You should feel comfortable with the work covered in this chapter before attempting to move onto the Grade 10 Geometry chapter, the Grade 10 Trigonometry chapter or the Grade 10 Analytical Geometry chapter. This chapter revises:

The two simplest objects in geometry are points and lines.

A point is a coordinate that marks a position in space (on a number line, on a plane or in three dimensions or even more) and is denoted by a dot. Points are usually labelled with a capital letter. Some examples of how points can be represented are shown in Figure 13.1.

A line is a continuous set of coordinates in space and can be thought of as being formed when many points are placed next to each other. Lines can be straight or curved, but are always continuous. This means that there are never any breaks in the lines (if there are, they would be distinct lines denoted separately). The endpoints of lines are labeled with capital letters. Examples of two lines are shown in Figure 13.1.

Figure 13.1. 

Examples of some points (labelled P, Q, R and S) and some lines (labelled BC and DE).

Lines are labelled according to the start point and end point. We call the line that starts at a point A and ends at a point B, AB. Since the line from point B to point A is the same as the line from point A to point B, we have that AB=BA.

When there is no ambiguity (which is the case throughout this text) the length of the line between points A and B is also denoted AB, the same as the notation to refer to the line itself. So if we say AB=CD we mean that the length of the line between A and B is equal to the length of the line between C and D.

Note: in higher mathematics, where there might be some ambiguity between when we want refer to the length of the line and when we just want to refer to the line itself, the notation |AB| is usually used to refer to the length of the line. In this case, if one says |AB|=|CD|, it means the lengths of the lines are the same, whereas if one says AB=CD, it means that the two lines actually coincide (i.e. they are the same). Throughout this text, however, this notation will not be used, and AB=CD ALWAYS implies that the lengths are the same.

A line is measured in units of length. Some common units of length are listed in Table 13.1.

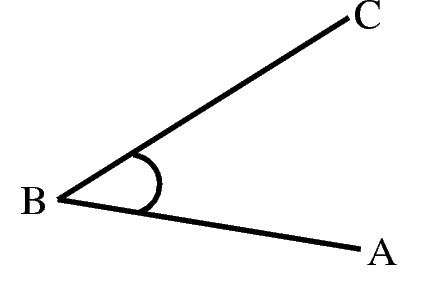
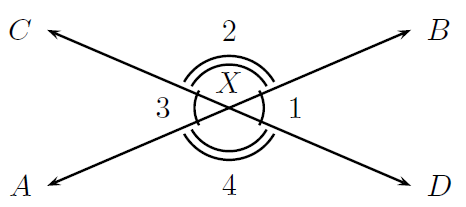
An angle is formed when two straight lines meet at a point. The point at which two lines meet is known as a vertex. Angles are labelled with a 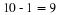called a caret on a letter. For example, in Figure 13.2 the angle is at 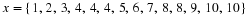. Angles can also be labelled according to the line segments that make up the angle. For example, in Figure 13.2 the angle is made up when line segments CB and BA meet. So, the angle can be referred to as ∠CBA or ∠ABC or, if there is no ambiguity (i.e. there is only one angle at B) sometimes simply ∠B. The ∠ symbol is a short method of writing angle in geometry.

Angles are measured in degrees which is denoted by ^∘, a small circle raised above the text in the same fashion as an exponent (or a superscript).

Figure 13.2. 

Angle labelled as , ∠CBA or ∠ABC

Figure 13.3. 

Examples of angles. , even though the lines making up the angles are of different lengths.

Measuring angles

The size of an angle does not depend on the length of the lines that are joined to make up the angle, but depends only on how both the lines are placed as can be seen in Figure 13.3. This means that the idea of length cannot be used to measure angles. An angle is a rotation around the vertex.

Using a Protractor

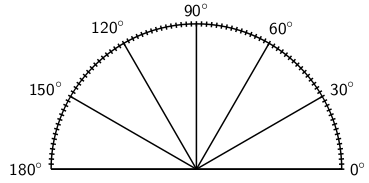
A protractor is a simple tool that is used to measure angles. A picture of a protractor is shown in Figure 13.4.

Figure 13.4. 

Diagram of a protractor.

Method:

Using a protractor

1. Place the bottom line of the protractor along one line of the angle so that the other line of the angle points at the degree markings.

2. Move the protractor along the line so that the centre point on the protractor is at the vertex of the two lines that make up the angle.

3. Follow the second line until it meets the marking on the protractor and read off the angle. Make sure you start measuring at 0^∘.

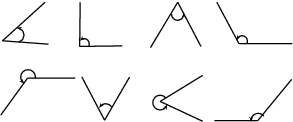
Measuring Angles : Use a protractor to measure the following angles:

Figure 13.5. 

Special Angles

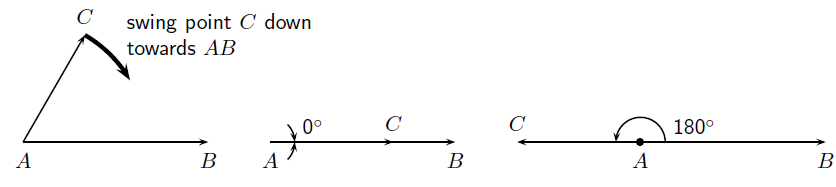
What is the smallest angle that can be drawn? The figure below shows two lines (CA and AB) making an angle at a common vertex A. If line CA is rotated around the common vertex A, down towards line AB, then the smallest angle that can be drawn occurs when the two lines are pointing in the same direction. This gives an angle of 0^∘. This is shown in Figure 13.6

Figure 13.6. 

If line CA is now swung upwards, any other angle can be obtained. If line CA and line AB point in opposite directions (the third case in Figure 13.6) then this forms an angle of 180^∘.

Tip

If three points A, B and C lie on a straight line, then the angle between them is 180^∘. Conversely, if the angle between three points is 180^∘, then the points lie on a straight line.

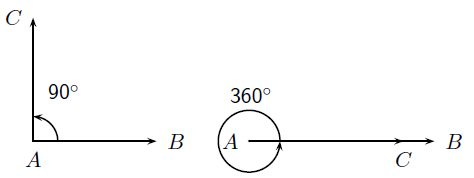
An angle of 90^∘ is called a right angle. A right angle is half the size of the angle made by a straight line (180^∘). We say CA is perpendicular to AB or CA⊥AB. An angle twice the size of a straight line is 360^∘. An angle measuring 360^∘ looks identical to an angle of 0^∘, except for the labelling. We call this a revolution.

Figure 13.7. 

An angle of 90^∘ is known as a right angle.

Angles larger than 360^∘

All angles larger than 360^∘ also look like we have seen them before. If you are given an angle that is larger than 360^∘, continue subtracting 360^∘ from the angle, until you get an answer that is between 0^∘and 360^∘. Angles that measure more than 360^∘ are largely for mathematical convenience.

Tip

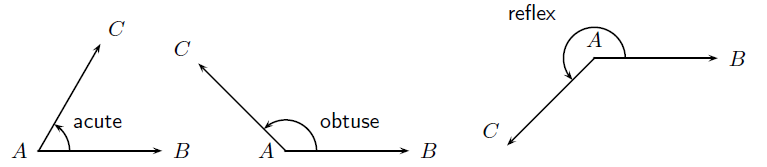
• Acute angle: An angle ≥0^∘ and <90^∘.

• Right angle: An angle measuring 90^∘.

• Obtuse angle: An angle >90^∘ and <180^∘.

• Straight angle: An angle measuring 180^∘.

• Reflex angle: An angle >180^∘ and <360^∘.

• Revolution: An angle measuring 360^∘.

These are simply labels for angles in particular ranges, shown in Figure 13.8.

Figure 13.8. 

Three types of angles defined according to their ranges.

Once angles can be measured, they can then be compared. For example, all right angles are 90^∘, therefore all right angles are equal and an obtuse angle will always be larger than an acute angle.

The following video summarizes what you have learnt so far about angles.

(This media type is not supported in this reader. Click to open media in browser.)

Figure 13.9. Khan Academy video on angles - 1

Note that for high school trigonometry you will be using degrees, not radians as stated in the video.

Special Angle Pairs

In Figure 13.10, straight lines AB and CD intersect at point X, forming four angles: or ∠BXD, or ∠BXC, or ∠CXA and or ∠AXD.

Figure 13.10. 

Two intersecting straight lines with vertical angles and .

The table summarises the special angle pairs that result.

Table 13.2.

Special Angle	Property	Example
adjacent angles	share a common vertex and a common side	, , ,
linear pair (adjacent angles on a straight line)	adjacent angles formed by two intersecting straight lines that by definition add to 180∘	; ; ;
opposite angles	angles formed by two intersecting straight lines that share a vertex but do not share any sides	; Page 1Page 2Page 3Page 4Page 5Page 6Page 7Page 8Page 9Page 10Page 11Page 12Page 13Page 14Page 15Page 16Page 17Page 18Page 19Page 20Page 21Page 22Page 23Page 24 PREV   NEXT × Sign up Log in