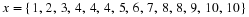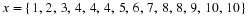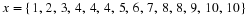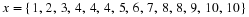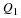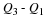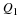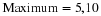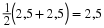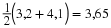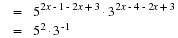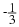Analytical geometry, also called co-ordinate geometry and earlier referred to as Cartesian geometry, is the study of geometry using the principles of algebra, and the Cartesian co-ordinate system. It is concerned with defining geometrical shapes in a numerical way, and extracting numerical information from that representation. Some consider that the introduction of analytic geometry was the beginning of modern mathematics.
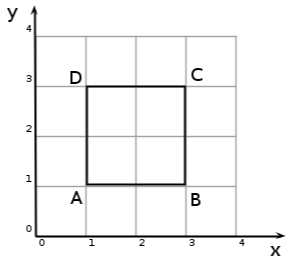
If we are given the co-ordinates of the vertices of a figure then we can draw that figure on the Cartesian plane. For example take quadrilateral ABCD with co-ordinates: A(1,1), B(1,3), C(3,3) and D(1,3) and represent it on the Cartesian plane. This is shown in Figure 16.1.
To represent any figure on the Cartesian plane, you place a dot at each given co-ordinate and then connect these points with straight lines. One point to note is in naming a figure. In the above example, we called the quadrilateral ABCD. This tells us that we move from point A, to point B, to point C, to point D and then back to point A again. So when you are asked to draw a figure on the Cartesian plane, you will follow this naming scheme. If you had the same points, and called it, for example, ACBD you would not get a quadrilateral but a pair of triangles instead. This is important. Sometimes you may be given only some of the points and you will then be required to find the other points using the work covered in the rest of this chapter.
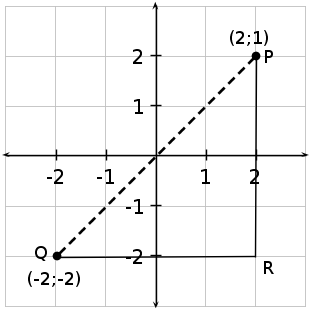
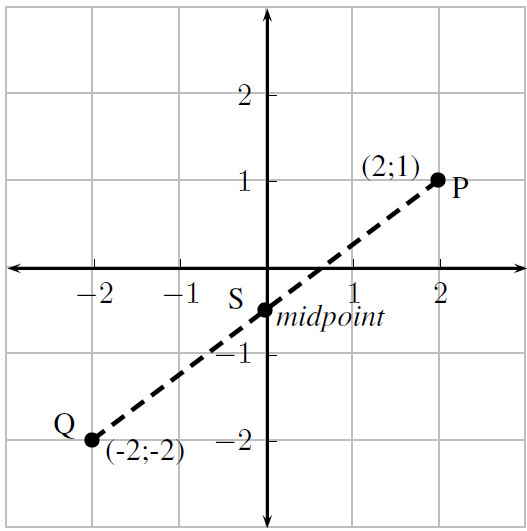
One of the simplest things that can be done with analytical geometry is to calculate the distance between two points. Distance is a number that describes how far apart two point are. For example, point P has co-ordinates (2,1) and point Q has co-ordinates (–2,–2). How far apart are points P and Q? In the figure, this means how long is the dashed line?
In the figure, it can be seen that the length of the line PR is 3 units and the length of the line QR is four units. However, the ▵PQR, has a right angle at R. Therefore, the length of the side PQ can be obtained by using the Theorem of Pythagoras:
The length of PQ is the distance between the points P and Q.
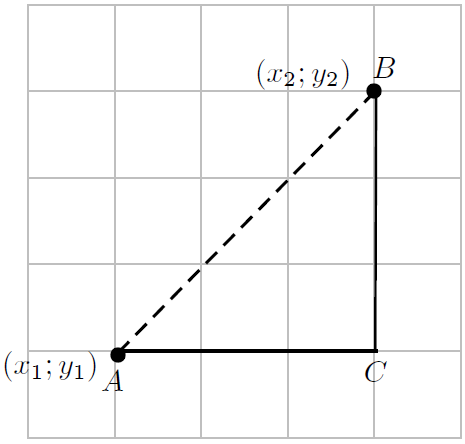
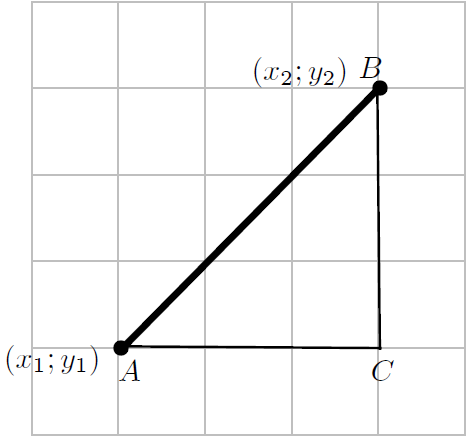
In order to generalise the idea, assume A is any point with co-ordinates 
and B is any other point with co-ordinates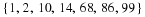 
.
The formula for calculating the distance between two points is derived as follows. The distance between the points A and B is the length of the line AB. According to the Theorem of Pythagoras, the length of AB is given by:
However,
Therefore,
Therefore, for any two points, 
and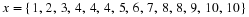 
, the formula is:
Using the formula, distance between the points P and Q with co-ordinates (2;1) and (-2;-2) is then found as follows. Let the co-ordinates of point P be 
and the co-ordinates of point Q be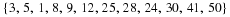 
. Then the distance is:
The following video provides a summary of the distance formula.
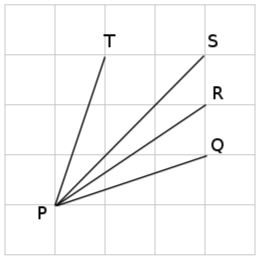
The gradient of a line describes how steep the line is. In the figure, line PT is the steepest. Line PS is less steep than PT but is steeper than PR, and line PR is steeper than PQ.
The gradient of a line is defined as the ratio of the vertical distance to the horizontal distance. This can be understood by looking at the line as the hypotenuse of a right-angled triangle. Then the gradient is the ratio of the length of the vertical side of the triangle to the horizontal side of the triangle. Consider a line between a point A with co-ordinates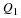 
and a point B with co-ordinates 
.
So we obtain the following for the gradient of a line:
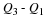
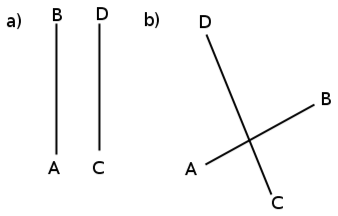
We can use the gradient of a line to determine if two lines are parallel or perpendicular. If the lines are parallel (Figure 16.7a) then they will have the same gradient, i.e. mAB=mCD. If the lines are perpendicular (Figure 16.7b) than we have: 
For example the gradient of the line between the points P and Q, with co-ordinates (2;1) and (-2;-2) (Figure 16.2) is:
The following video provides a summary of the gradient of a line.
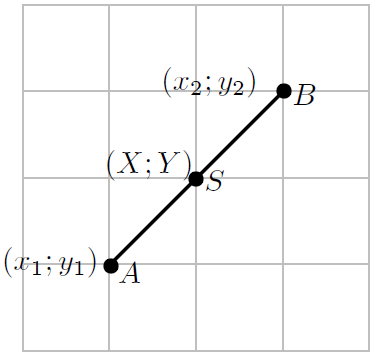
Sometimes, knowing the co-ordinates of the middle point or midpoint of a line is useful. For example, what is the midpoint of the line between point P with co-ordinates (2;1) and point Q with co-ordinates (–2;–2).
The co-ordinates of the midpoint of any line between any two points A and B with co-ordinates 
and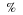 
, is generally calculated as follows. Let the midpoint of AB be at point S with co-ordinates (X;Y). The aim is to calculate X and Y in terms of 
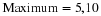and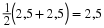 
.
Then the co-ordinates of the midpoint (S) of the line between point P with co-ordinates (2;1) and point Q with co-ordinates (–2;–2) is:
It can be confirmed that the distance from each end point to the midpoint is equal. The co-ordinate of the midpoint S is (0;–0,5).
and
It can be seen that PS=QS as expected.
The following video provides a summary of the midpoint of a line.
Figures can be represented on the Cartesian plane
The formula for finding the distance between two points is:
The formula for finding the gradient of a line is:
The formula for finding the midpoint between two points is:
If two lines are parallel then they will have the same gradient, i.e. mAB=mCD. If two lines are perpendicular than we have: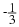 
Represent the following figures on the Cartesian plane:
Triangle DEF with D(1;2), E(3;2) and F(2;4)
Quadrilateral GHIJ with G(2;-1), H(0;2), I(-2;-2) and J(1;-3)
Quadrilateral MNOP with M(1;1), N(-1;3), O(-2;3) and P(-4;1)
Quadrilateral WXYZ with W(1;-2), X(-1;-3), Y(2;-4) and Z(3;-2)
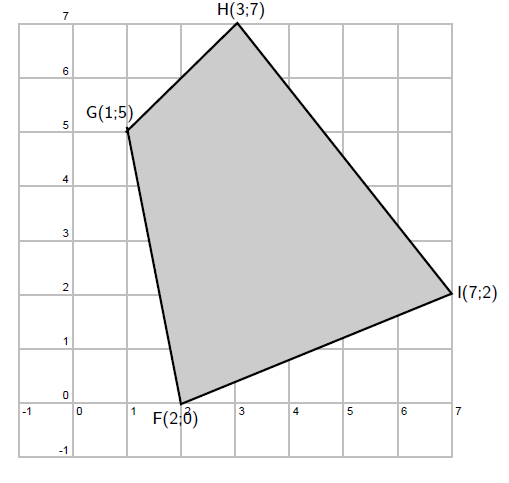
In the diagram given the vertices of a quadrilateral are F(2;0), G(1;5), H(3;7) and I(7;2).
What are the lengths of the opposite sides of FGHI?
Are the opposite sides of FGHI parallel?
Do the diagonals of FGHI bisect each other?
Can you state what type of quadrilateral FGHI is? Give reasons for your answer.
A quadrialteral ABCD with vertices A(3;2), B(1;7), C(4;5) and D(1;3) is given.
Draw the quadrilateral.
Find the lengths of the sides of the quadrilateral.
ABCD is a quadrilateral with verticies A(0;3), B(4;3), C(5;-1) and D(-1;-1).
Show that:
AD = BC
AB ∥ DC
What name would you give to ABCD?
Show that the diagonals AC and BD do not bisect each other.
P, Q, R and S are the points (-2;0), (2;3), (5;3), (-3;-3) respectively.
Show that:
SR = 2PQ
SR ∥ PQ
Calculate:
PS
QR
What kind of a quadrilateral is PQRS? Give reasons for your answers.
EFGH is a parallelogram with verticies E(-1;2), F(-2;-1) and G(2;0). Find the co-ordinates of H by using the fact that the diagonals of a parallelogram bisect each other.
Click here for the solution
PQRS is a quadrilateral with points P(0; −3) ; Q(−2;5) ; R(3;2) and S(3;–2) in the Cartesian plane.
Find the length of QR.
Find the gradient of PS.
Find the midpoint of PR.
Is PQRS a parallelogram? Give reasons for your answer.
A(–2;3) and B(2;6) are points in the Cartesian plane. C(a;b) is the midpoint of AB. Find the values of a and b.
Click here for the solution
Consider: Triangle ABC with vertices A (1; 3) B (4; 1) and C (6; 4):
Sketch triangle ABC on the Cartesian plane.
Show that ABC is an isoceles triangle.
Determine the co-ordinates of M, the midpoint of AC.
Determine the gradient of AB.
Show that the following points are collinear: A, B and D(7;-1)
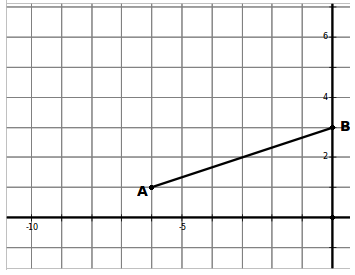
In the diagram, A is the point (-6;1) and B is the point (0;3)
Find the equation of line AB
Calculate the length of AB
A’ is the image of A and B’ is the image of B. Both these images are obtain by applying the transformation: (x;y)→(x-4;y-1). Give the coordinates of both A’ and B’
Find the equation of A’B’
Calculate the length of A’B’
Can you state with certainty that AA'B'B is a parallelogram? Justify your answer.