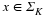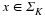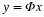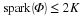This module provides a brief overview of the relationship between model selection, sparse linear regression, and the techniques developed in compressive sensing.
Many of the sparse recovery algorithms we have described so far in this course were originally developed to address the problem of sparse linear regression and model selection in statistics. In this setting we are given some data consisting of a set of input variables and response variables. We will suppose that there are a total of N input variables, and we observe a total of M input and response pairs. We can represent the set of input variable observations as an M×N matrix Φ, and the set of response variable observations as an M×1 vector y.
In linear regression, it is assumed that y can be approximated as a linear function of the input variables, i.e., there exists an x such that y≈Φx. However, when the number of input variables is large compared to the number of observations, i.e., M≪N, this becomes extremely challenging because we wish to estimate N parameters from far fewer than N observations. In general this would be impossible to overcome, but in practice it is common that only a few input variables are actually necessary to predict the response variable. In this case the x that we wish to estimate is sparse, and we can apply all of the techniques that we have learned so far for sparse recovery to estimate x. In this setting, not only does sparsity aid us in our goal of obtaining a regression, but it also performs model selection by identifying the most relevant variables in predicting the response.
This module illustrates the application of the ideas of compressive sensing to the design and decoding of error correcting codes for vectors of real numbers subject to sparse corruptions.
In communications, error correction refers to mechanisms that can detect and correct errors in the data that appear duet to distortion in the transmission channel. Standard approaches for error correction rely on repetition schemes, redundancy checks, or nearest neighbor code search. We consider the particular case in which a signal x with M entries is coded by taking length-N linearly independent codewords 
, with N>M and summing them using the entries of x as coefficients. The received message is a length-N code y=∑Mm=1φixi=Φf, where Φ is a matrix that has the different codewords for columns. We assume that the transmission channel corrupts the entries of y in an additive way, so that the received data is y=Φx+e, where e is an error vector.
The techniques developed for sparse recovery in the context of compressive sensing (CS) provide a number of methods to estimate the error vector e — therefore making it possible to correct it and obtain the signal x — when e is sufficiently sparse 1. To estimate the error, we build a matrix Θ that is a basis for the orthogonal subspace to the span of the matrix Φ, i.e., an (N–M)×N matrix Θ that holds ΘΦ=0. When such a matrix is obtained, we can modify the measurements by multiplying them with the matrix to obtain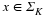 
. If the matrix Θ is well-suited for CS (i.e., it satisfies a condition such as the restricted isometry property) and e is sufficiently sparse, then the error vector e can be estimated accurately using CS. Once the estimate 
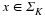is obtained, the error-free measurements can be estimated as 
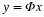, and the signal can be recovered as 
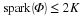. As an example, when the codewords φm have random independent and identically distributed sub-Gaussian entries, then a K-sparse error can be corrected if M<N–CKlogN/K for a fixed constant C (see "Matrices that satisfy the RIP").
Candès, E. and Rudelson, M. and Tao, T. and Vershynin, R. (2005, Oct.). Error correction via linear programming. In Proc. IEEE Symp. Found. Comp. Science (FOCS). Pittsburg, PA
This module provides an overview of the relationship between compressive sensing and problems in theoretical computer science including combinatorial group testing and computation on data streams.
Another scenario where compressive sensing and sparse recovery algorithms can be potentially useful is the context of group testing and the related problem of computation on data streams.
Among the historically oldest of all sparse recovery algorithms were developed in the context of combinatorial group testing 2, 3, 5. In this problem we suppose that there are N total items and K anomalous elements that we wish to find. For example, we might wish to identify defective products in an industrial setting, or identify a subset of diseased tissue samples in a medical context. In both of these cases the vector x indicates which elements are anomalous, i.e., xi≠0 for the K anomalous elements and xi=0 otherwise. Our goal is to design a collection of tests that allow us to identify the support (and possibly the values of the nonzeros) of x while also minimizing the number of tests performed. In the simplest practical setting these tests are represented by a binary matrix Φ whose entries φij are equal to 1 if and only if the j th item is used in the i th test. If the output of the test is linear with respect to the inputs, then the problem of recovering the vector x is essentially the same as the standard sparse recovery problem in compressive sensing.
Another application area in which ideas related to compressive sensing have proven useful is computation on data streams 1, 4. As an example of a typical data streaming problem, suppose that xi represents the number of packets passing through a network router with destination i. Simply storing the vector x is typically infeasible since the total number of possible destinations (represented by a 32-bit IP address) is N=232. Thus, instead of attempting to store x directly, one can store y=Φx where Φ is an M×N matrix with M≪N. In this context the vector y is often called a sketch. Note that in this problem y is computed in a different manner than in the compressive sensing context. Specifically, in the network traffic example we do not ever observe xi directly, rather we observe increments to xi (when a packet with destination i passes through the router). Thus we construct y iteratively by adding the i th column to y each time we observe an increment to xi, which we can do since y=Φx is linear. When the network traffic is dominated by traffic to a small number of destinations, the vector x is compressible, and thus the problem of recovering x from the sketch Φx is again essentially the same as the sparse recovery problem in compressive sensing.
Cormode, G. and Hadjieleftheriou, M. (2009). Finding the frequent items in streams of data. Comm. ACM, 52(10), 97–105.
Erlich, Y. and Shental, N. and Amir, A. and Zuk, O. (2009, Sept.). Compressed sensing approach for high throughput carrier screen. In Proc. Allerton Conf. Communication, Control, and Computing. Monticello, IL
Kainkaryam, R. and Breux, A. and Gilbert, A. and Woolf, P. and Schiefelbein, J. (2010). poolMC: Smart pooling of mRNA samples in microarray experiments. BMC Bioinformatics, 11(1), 299.
Muthukrishnan, S. (2005). Found. Trends in Theoretical Comput. Science: Vol. 1. Data Streams: Algorithms and Applications. (). Boston, MA: Now Publishers.
Shental, N. and Amir, A. and Zuk, O. (2009). Identification of rare alleles and their carriers using compressed se(que)nsing. Nucleic Acids Research, 38(19), e179.
This module describes the application of compressive sensing to problems in medical imaging.
Magnetic Resonance Imaging (MRI) is a medical imaging technique based on the core principle that protons in water molecules in the human body align themselves in a magnetic field. MRI machines repeatedly pulse magnetic fields to cause water molecules in the human body to disorient and then reorient themselves, which causes a release of detectable radiofrequencies. We assume that the object to be imaged as a collection of voxels. The MRI's magnetic pulses are sent incrementally along a gradient leading to a different phase and frequency encoding for each column and row of voxels respectively. Abstracting away from the technicalities of the physical process, the magnetic field measured in MRI acquisition corresponds to a Fourier coefficient of the imaged object; the object can then be recovered by an inverse Fourier transform. , we can view the MRI as measuring Fourier samples.
A major limitation of the MRI process is the linear relation between the number of measured data samples and scan times. Long-duration MRI scans are more susceptible to physiological motion artifacts, add discomfort to the patient, and are expensive 3. Therefore, minimizing scan time without compromising image quality is of direct benefit to the medical community.
The theory of compressive sensing (CS) can be applied to MR image reconstruction by exploiting the transform-domain sparsity of MR images 4, 5, 6, 7. In standard MRI reconstruction, undersampling in the Fourier domain results in aliasing artifacts when the image is reconstructed. However, when a known transform renders the object image sparse or compressible, the image can be reconstructed using sparse recovery methods. While the discrete cosine and wavelet transforms are commonly used in CS to reconstruct these images, the use of total variation norm minimization also provides high-quality reconstruction.
Electroencephalography (EEG) and Magnetoencephalography (MEG) are two popular noninvasive methods to characterize brain function by measuring scalp electric potential distributions and magnetic fields due to neuronal firing. EEG and MEG provide temporal resolution on the millisecond timescale characteristic of neural population activity and can also help to estimate the current sources inside the brain by solving an inverse problem 1.
Models for neuromagnetic sources suggest that the underlying activity is often limited in spatial extent. Based on this idea, algorithms like FOCUSS (Focal Underdetermined System Solution) are used to identify highly localized sources by assuming a sparse model to solve an underdetermined problem 2.
FOCUSS is a recursive linear estimation procedure, based on a weighted pseudo-inverse solution. The algorithm assigns a current (with nonlinear current location parameters) to each element within a region so that the unknown current values can be related linearly to the measurements. The weights at each step are derived from the solution of the previous iterative step. The algorithm converges to a source distribution in which the number of parameters required to describe source currents does not exceed the number of measurements. The initialization determines which of the localized solutions the algorithm converges to.
Gorodnitsky, I. and George, J. and Rao, B. (1995). Neuromagnetic source imaging with FOCUSS: A recursive weighted minimum norm algorithm. Electroencephalography and Clinical Neurophysiology, 95(4), 231–251.
Gorodnitsky, I. and Rao, B. (1993, Nov.). Convergence analysis of a class of adaptive weighted norm extrapolation algorithms. In Proc. Asilomar Conf. Signals, Systems, and Computers. Pacific Grove, CA
Lustig, M. and Donoho, D. and Pauly, J. (2006, May). Rapid MR Imaging with Compressed Sensing and Randomly Under-Sampled 3DFT Trajectories. In Proc. Annual Meeting of ISMRM. Seattle, WA
Lustig, M. and Lee, J. and Donoho, D. and Pauly, J. (2005, May). Faster Imaging with Randomly Perturbed, Under-Sampled Spirals and Reconstruction. In Proc. Annual Meeting of ISMRM. Miami, FL
Lustig, M. and Lee, J. and Donoho, D. and Pauly, J. (2006, May). k-t SPARSE: High Frame Rate Dynamic MRI Exploiting Spatio-Temporal Sparsity. In Proc. Annual Meeting of ISMRM. Seattle, WA
Lustig, M. and Santos, J. and Lee, J. and Donoho, D. and Pauly, J. (2005, Nov.). Application of Compressed Sensing for Rapid MR Imaging. In Proc. Work. Struc. Parc. Rep. Adap. Signaux (SPARS). Rennes, France
Trzasko, J. and Manduca, A. (2009). Highly Undersampled Magnetic Resonance Image Reconstruction via Homotopic -Minimization. IEEE Trans. Med. Imaging, 28(1), 106–121.
In this module we describe the random demodulator and how it can be used in the application of the theory of compressive sensing to the problem of acquiring a high-bandwidth continuous-time signal.
We now consider the application of compressive sensing (CS) to the problem of designing a system that can acquire a continuous-time signal x(t). Specifically, we would like to build an analog-to-digital converter (ADC) that avoids having to sample x(t) at its Nyquist rate whe