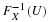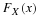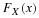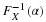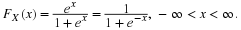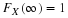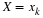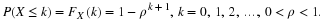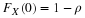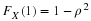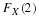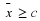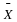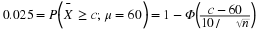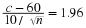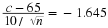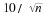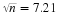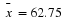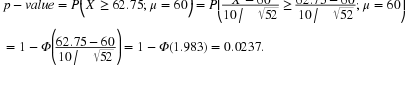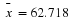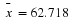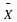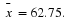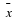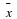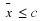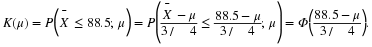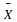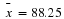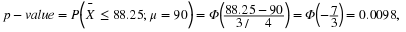Suppose a manufacturer of a certain printed circuit observes that about p=0.05 of the circuits fails. An engineer and statistician working together suggest some changes that might improve the design of the product. To test this new procedure, it was agreed that n=100 circuits would be produced using the proposed method and the checked. Let Y equal the number of these 200 circuits that fail. Clearly, if the number of failures, Y, is such that Y/200 is about to 0.05, then it seems that the new procedure has not resulted in an improvement. On the other hand, If Y is small so that Y/200 is about 0.01 or 0.02, we might believe that the new method is better than the old one. On the other hand, if Y/200 is 0.08 or 0.09, the proposed method has perhaps caused a greater proportion of failures.
What is needed is to establish a formal rule that tells when to accept the new procedure as an improvement. For example, we could accept the new procedure as an improvement if
Y≤5
of
Y/n≤0.025
. We do note, however, that the probability of the failure could still be about p=0.05 even with the new procedure, and yet we could observe 5 of fewer failures in n=200 trials.
That is, we would accept the new method as being an improvement when, in fact, it was not. This decision is a mistake which we call a Type I error. On the other hand, the new procedure might actually improve the product so that p is much smaller, say p=0.02, and yet we could observe y=7 failures so that y/200=0.035. Thus we would not accept the new method as resulting in an improvement when in fact it had. This decision would also be a mistake which we call a Type II error.
If it we believe these trials, using the new procedure, are independent and have about the same probability of failure on each trial, then Y is binomial
b(
200,p
)
. We wish to make a statistical inference about p using the unbiased 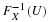 . We could also construct a confidence interval, say one that has 95% confidence, obtaining
. We could also construct a confidence interval, say one that has 95% confidence, obtaining 
This inference is very appropriate and many statisticians simply do this. If the limits of this confidence interval contain 0.05, they would not say the new procedure is necessarily better, al least until more data are taken. If, on the other hand, the upper limit of this confidence interval is less than 0.05, then they fell 95% confident that the true p is now less than 0.05.
Here, in this illustration, we are testing whether or not the probability of failure has or has not decreased from 0.05 when the new manufacturing procedure is used.
The no change hypothesis,
H0
:p=0.05
, is called the null hypothesis. Since
H0
:p=0.05
completely specifies the distribution it is called a simple hypothesis; thus
H0
:p=0.05
is a simple null hypothesis.
The research worker’s hypothesis
H1
:p<0.05
is called the alternative hypothesis. Since
H1
:p<0.05
does not completely specify the distribution, it is a composite hypothesis because it is composed of many simple hypotheses.
The rule of rejecting
H0 and accepting
H1 if
Y≤5
, and otherwise accepting
H0 is called a test of a statistical hypothesis.
It is clearly seen that two types of errors can be recorded
Type I error: Rejecting
H0 and accepting
H1, when
H0 is true;
Type II error: Accepting
H0 when
H1
is true, that is, when
H0 is false.
Since, in the example above, we make a Type I error if
Y≤5
when in fact p=0.05. we can calculate the probability of this error, which we denote by
α
and call the significance level of the test. Under an assumption, it is  .
.
Since n is rather large and p is small, these binomial probabilities can be approximated extremely well by Poisson probabilities with
λ=200(
0.05
)=10.
That is, from the Poisson table, the probability of the Type I error is 
Thus, the approximate significance level of this test is
α=0.067
. This value is reasonably small. However, what about the probability of Type II error in case p has been improved to 0.02, say? This error occurs if
Y>5
when, in fact, p=0.02; hence its probability, denoted by
β
, is 
Again we use the Poisson approximation, here
λ=200(0.02)=4
, to obtain 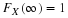
The engineers and the statisticians who created this new procedure probably are not too pleased with this answer. That is, they note that if their new procedure of manufacturing circuits has actually decreased the probability of failure to 0.02 from 0.05 (a big improvement), there is still a good chance, 0.215, that
H0
: p=0.05
is accepted and their improvement rejected. Thus, this test of
H0
: p=0.05
against
H1
: p=0.02
is unsatisfactory.
Without worrying more about the probability of the Type II error, here, above was presented a frequently used procedure for testing
H0
: p=p
0, where
p0 is some specified probability of success. This test is based upon the fact that the number of successes, Y, in n independent Bernoulli trials is such that
Y/n
has an approximate normal distribution,
N[p
0
, p
0
(1- p
0
)/n]
, provided
H0
: p=p
0 is true and n is large.
Suppose the alternative hypothesis is
H0
: p>p
0
; that is, it has been hypothesized by a research worker that something has been done to increase the probability of success. Consider the test of
H0
: p=p
0 against
H1
: p> p
0 that rejects
H0 and accepts
H1 if and only if
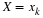
That is, if
Y/n
exceeds
p0 by standard deviations of
Y/n
, we reject
H0 and accept the hypothesis
H1
: p> p
0. Since, under
H0 Z is approximately
N(
0,1
)
, the approximate probability of this occurring when
H0
: p=p
0 is true is
α
. That is the significance level of that test is approximately
α
. If the alternative is
H1
: p< p
0 instead of
H1
: p> p
0, then the appropriate
α
-level test is given by
Z≤−zα. That is, if
Y/n
is smaller than
p0 by standard deviations of
Y/n
, we accept
H1
: p< p
0.
In general, without changing the sample size or the type of the test of the hypothesis, a decrease in
α
causes an increase in
β
, and a decrease in
β
causes an increase in
α
. Both probabilities
α
and
β
of the two types of errors can be decreased only by increasing the sample size or, in some way, constructing a better test of the hypothesis.
If n=100 and we desire a test with significance level
α
=0.05, then 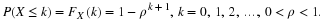 means, since
means, since 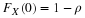 is
N(μ,100/100=1)
,
is
N(μ,100/100=1)
,
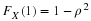 and
c−60=1.645
. Thus c=61.645. The power function is
and
c−60=1.645
. Thus c=61.645. The power function is
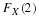
In particular, this means that
β
at
μ
=65 is
=1−K(
μ
)=Φ(
61.645−65
)=Φ(
−3.355
)≈0;
so, with n=100, both
α
and
β
have decreased from their respective original values of 0.1587 and 0.0668 when n=25. Rather than guess at the value of n, an ideal power function determines the sample size. Let us use a critical region of the form 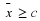 . Further, suppose that we want
α
=0.025 and, when
μ
=65,
β
=0.05. Thus, since
. Further, suppose that we want
α
=0.025 and, when
μ
=65,
β
=0.05. Thus, since 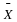 is
N(μ,100/n)
,
is
N(μ,100/n)
,
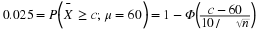 and
and 
That is, 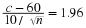 and
and 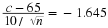 .
.
Solving these equations simultaneously for c and 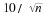 , we obtain
, we obtain 

Thus, 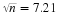 and
n=51.98
. Since n must be an integer, we would use n=52 and obtain
α
=0.025 and
β
=0.05, approximately.
and
n=51.98
. Since n must be an integer, we would use n=52 and obtain
α
=0.025 and
β
=0.05, approximately.
For a number of years there has been another value associated with a statistical test, and most statistical computer programs automatically print this out; it is called the probability value or, for brevity, p-value. The p-value associated with a test is the probability that we obtain the observed value of the test statistic or a value that is more extreme in the direction of the alternative hypothesis, calculated when
H0 is true. Rather than select the critical region ahead of time, the p-value of a test can be reported and the reader then makes a decision.
Say we are testing
H0
: μ=60
against
H1
: μ>60
with a sample mean  based on n=52 observations. Suppose that we obtain the observed sample mean of
based on n=52 observations. Suppose that we obtain the observed sample mean of  . If we compute the probability of obtaining an
. If we compute the probability of obtaining an  of that value of 62.75 or greater when
μ
=60, then we obtain the p-value associated with
of that value of 62.75 or greater when
μ
=60, then we obtain the p-value associated with 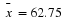 . That is,
. That is,
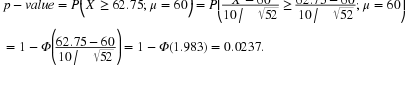
If this p-value is small, we tend to reject the hypothesis
H0
: μ=60
. For example, rejection of
H0
: μ=60
if the p-value is less than or equal to 0.025 is exactly the same as rejection if 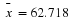 .That is,
.That is, 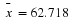 has a p-value of 0.025. To help keep the definition of p-value in mind, we note that it can be thought of as that tail-end probability, under
H0, of the distribution of the statistic, here
has a p-value of 0.025. To help keep the definition of p-value in mind, we note that it can be thought of as that tail-end probability, under
H0, of the distribution of the statistic, here 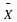 , beyond the observed value of the statistic. See Figure 1 for the p-value associated with
, beyond the observed value of the statistic. See Figure 1 for the p-value associated with 
Example 4.1.
Suppose that in the past, a golfer’s scores have been (approximately) normally distributed with mean
μ
=90 and
σ2=9. After taking some lessons, the golfer has reason to believe that the mean
μ
has decreased. (We assume that
σ2 is still about 9.) To test the null hypothesis
H0
: μ=90
against the alternative hypothesis
H1
: μ<90
, the golfer plays 16 games, computing the sample mean 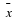 .If
.If 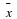 is small, say
is small, say 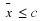 , then
H0 is rejected and
H1 accepted; that is, it seems as if the mean
μ
has actually decreased after the lessons. If c=88.5, then the power function of the test is
, then
H0 is rejected and
H1 accepted; that is, it seems as if the mean
μ
has actually decreased after the lessons. If c=88.5, then the power function of the test is
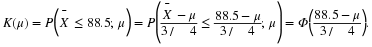
Because 9/16 is the variance of  . In particular,
α=K(
90
)=Φ(
−2
)=1−0.9772=0.0228.
. In particular,
α=K(
90
)=Φ(
−2
)=1−0.9772=0.0228.
If, in fact, the true mean is equal to
μ
=88 after the lessons, the power is
K(
88
)=Φ(
2/3
)=0.7475
. If
μ
=87, then
K(
87
)=Φ(
2
)=0.9772
. An observed sample mean of 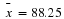 has a
has a
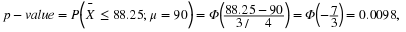
and this would lead to a rejection at
α
=0.0228 (or even
α
=0.01).