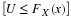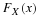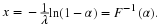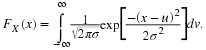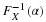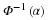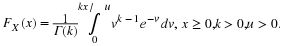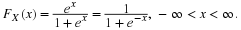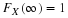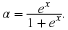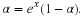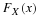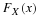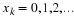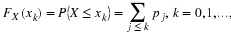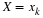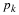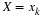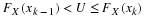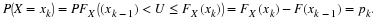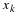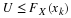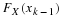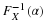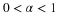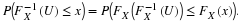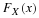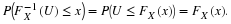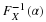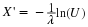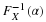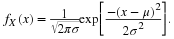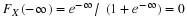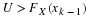Once a model is specified with its parameters and data have been collected, one is in a position to evaluate the model’s goodness of fit, that is, how well the model fits the observed pattern of data. Finding parameter values of a model that best fits the data — a procedure called parameter estimation, which assesses goodness of fit.
There are two generally accepted methods of parameter estimation. They are least squares estimation (LSE) and maximum likelihood estimation (MLE). The former is well known as linear regression, the sum of squares error, and the root means squared deviation is tied to the method. On the other hand, MLE is not widely recognized among modelers in psychology, though it is, by far, the most commonly used method of parameter estimation in the statistics community.
LSE might be useful for obtaining a descriptive measure for the purpose of summarizing observed data, but MLE is more suitable for statistical inference such as model comparison. LSE has no basis for constructing confidence intervals or testing hypotheses whereas both are naturally built into MLE.
UNBIASED AND BIASED ESTIMATORS
Let consider random variables for which the functional form of the p.d.f. is know, but the distribution depends on an unknown parameter
θ
, that may have any value in a set
θ
, which is called the parameter space. In estimation the random sample from the distribution is taken to elicit some information about the unknown parameter
θ.
The experiment is repeated n independent times, the sample
X1
,X2
,...,Xn
is observed and one try to guess the value of
θ
using the observations
x1
,x2
,...xn
.
The function of
X1
,X2
,...,Xn
used to guess
θ
is called an estimator of
θ
. We want it to be such that the computed estimate 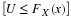 is usually close to
θ.
Let
is usually close to
θ.
Let 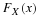 be an estimator of
θ. If Y to be a good estimator of
θ
, a very desirable property is that it means be equal to
θ
, namely
E(
Y
)=θ
.
be an estimator of
θ. If Y to be a good estimator of
θ
, a very desirable property is that it means be equal to
θ
, namely
E(
Y
)=θ
.
- Definition:
If 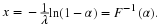 is called an unbiased estimator of
θ
. Otherwise, it is said to be biased.
is called an unbiased estimator of
θ
. Otherwise, it is said to be biased.
It is required not only that an estimator has expectation equal to
θ
, but also the variance of the estimator should be as small as possible.
If there are two unbiased estimators of
θ
, it could be probably possible to choose the one with the smaller variance. In general, with a random sample
X1
,X2
,...,Xn
of a fixed sample size n, a statistician might like to find the estimator 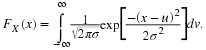 of an unknown parameter
θ
which minimizes the mean (expected) value of the square error (difference) Y−θ that is, minimizes
of an unknown parameter
θ
which minimizes the mean (expected) value of the square error (difference) Y−θ that is, minimizes
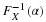
The statistic Y that minimizes 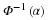 is the one with minimum mean square error. If we restrict our attention to unbiased estimators only, then
is the one with minimum mean square error. If we restrict our attention to unbiased estimators only, then 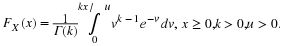 and the unbiased statistics Y that minimizes this expression is said to be the unbiased minimum variance estimator of
θ
.
and the unbiased statistics Y that minimizes this expression is said to be the unbiased minimum variance estimator of
θ
.