1992
4
1.1
1996
0.173
0.13
2000
0.006849
0.015
2004
0.001149
0.0018
Try it Now
2. The table below shows the value V, in billions of dollars, of US imports from China
t years after 2000.
year
2000
2001
2002
2003
2004
2005
t
0
1
2
3
4
5
V
100
102.3
125.2
152.4
196.7
243.5
Thi
s data appears to be growing exponentially. Linearize this data and build a model to
predict how many billions of dollars of imports were expected in 2011.
Important Topics of this Section
Semi-log graph
Log-log graph
Linearizing exponential functions
Fitting an exponential equation to data
Try it Now Answers
1.
x
f ( x) =
(
100
)
3162
.
0
2.
t
V t() =
1
(
545
.
90
)
2078
.
. Predicting in 2011, V
)
11
(
=
45
.
722
billion dollars
Section 4.7 Fitting Exponential Models to Data 295
Section 4.7 Exercises
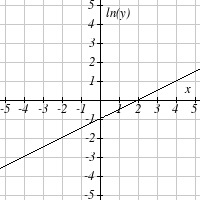
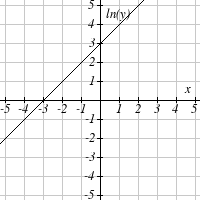
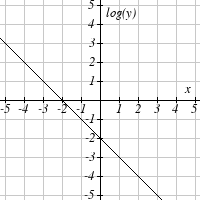
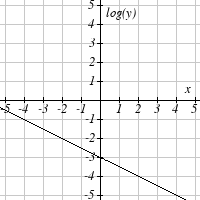
Graph each function on a semi-log scale, then find a formula for the linearized function in the
form log( f ( x)) = mx + b .
1. ( ) 4(1.3) x
f x =
2. ( ) 2(1.5) x
f x =
3. ( ) 10(0.2) x
f x =
4. ( ) 30(0.7) x
f x =
The graph below is on a semi-log scale, as indicated. Find a formula for the exponential function
y( x) .
5.
6.
7.
8.
Use regression to find an exponential function that best fits the data given.
9. x 1 2 3 4 5 6
y 1125 1495 2310 3294 4650 6361
10.
x 1
2
3
4
5
6
y 643 829 920 1073 1330 1631
11.
x 1
2
3
4
5
6
y 555 383 307 210 158 122
296 Chapter 4
12.
x 1
2
3
4
5
6
y 699 701 695 668 683 712
13. Total expenditures (in billions of dollars) in the US for nursing home care are shown below.
Use regression to find an exponential function that models the data. What does the model
predict expenditures will be in 2015?
Year
1990
1995
2000
2003
2005
2008
Expenditure 53
74
95
110
121
138
14. Light intensity as it passes through water decreases exponentially with depth. The data
below shows the light intensity (in lumens) at various depths. Use regression to find an
function that models the data. What does the model predict the intensity will be at 25 feet?
Depth (ft)
3
6
9
12
15
18
Lumen
11.5
8.6
6.7
5.2
3.8
2.9
15. The average price of electricity (in cents per kilowatt hour) from 1990 through 2008 is given
below. Determine if a linear or exponential model better fits the data, and use the better
model to predict the price of electricity in 2014.
Year 1990 1992 1994 1996 1998 2000 2002 2004 2006 2008
Cost 7.83 8.21 8.38 8.36 8.26 8.24 8.44 8.95 10.40 11.26
16. The average cost of a loaf of white bread from 1986 through 2008 is given below. Determine
if a linear or exponential model better fits the data, and use the better model to predict the
price of a loaf of bread in 2016.
Year 1986 1988 1990 1995 1997 2000 2002 2004 2006 2008
Cost 0.57 0.66 0.70 0.84 0.88 0.99 1.03 0.97 1.14 1.42
Chapter 5: Trigonometric Functions of Angles
In the previous chapters we have explored a variety of functions which could be
combined to form a variety of shapes. In this discussion, one common shape has been
missing: the circle. We already know certain things about the circle, like how to find area
and circumference, and the relationship between radius and diameter, but now, in this
chapter, we explore the circle and its unique features that lead us into the rich world of
trigonometry.
Section 5.1 Circles ...................................................................................................... 297
Section 5.2 Angles ...................................................................................................... 307
Section 5.3 Points on Circles using Sine and Cosine.................................................. 321
Section 5.4 The Other Trigonometric Functions ........................................................ 333
Section 5.5 Right Triangle Trigonometry ................................................................... 343
Section 5.1 Circles
To begin, we need to remember how to find distances. Starting with the Pythagorean
Theorem, which relates the sides of a right triangle, we can find the distance between two
points.
Pythagorean Theorem
The Pythagorean Theorem states that the sum of the squares of the legs of a right
triangle will equal the square of the hypotenuse of the triangle.
In graphical form, given the triangle shown, 2
2
2
a
c
+ b = c .
a
b
We can use the Pythagorean Theorem to find the distance between two points on a graph.
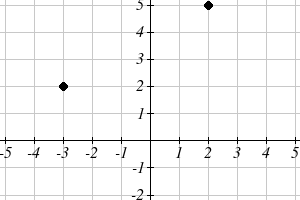
Example 1
Find the distance between the points (-3, 2) and (2, 5).
By plotting these points on the plane, we can then
draw a right triangle with these points at each end
of the hypotenuse. We can calculate horizontal
width of the triangle to be 5 and the vertical height
to be 3. From these we can find the distance
between the points using the Pythagorean
Theorem:
2
dist = 52 + 32 = 34
dist = 34
This chapter is part of Precalculus: An Investigation of Functions © Lippman & Rasmussen 2011.
This material is licensed under a Creative Commons CC-BY-SA license.
298 Chapter 5
Notice that the width of the triangle was calculated using the difference between the x
(input) values of the two points, and the height of the triangle was found using the
difference between the y (output) values of the two points. Generalizing this process
gives us the general distance formula.
Distance Formula
The distance between two points ( x y and ( x y can be calculated as
2 , 2 )
1 , 1 )
2
2
dist = ( x − x ) + ( y − y )
2
1
2
1
Try it Now
1. Find the distance between the points (1, 6) and (3, -5).
Circles
If we wanted to find an equation to represent a circle with
( x, y)
a radius of r centered at a point ( h, k), we notice that the
r
distance between any point ( x, y) on the circle and the
center point is always the same: r. Noting this, we can
use our distance formula to write an equation for the
( h, k)
radius:
2
2
r = ( x − h) + ( y − k)
Squaring both sides of the equation gives us the standard equation for a circle.
Equation of a Circle
The equation of a circle centered at the point ( h, k) with radius r can be written as 2
2
2
( x − h) + ( y − k) = r
Notice that a circle does not pass the vertical line test. It is not possible to write y as a
function of x or vice versa.
Example 2
Write an equation for a circle centered at the point (-3, 2) with radius 4.
Using the equation from above, h = -3, k = 2, and the radius r = 4. Using these in our formula, 2
2
2
( x − (− ))
3
+ ( y − )
2 = 4
simplified a bit, this gives
( x + )
3 2 + ( y − )
2 2 = 16
Section 5.1 Circles 299
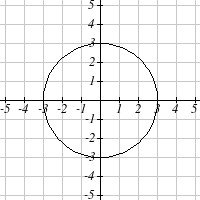
Example 3
Write an equation for the circle graphed here.
This circle is centered at the origin, the point (0, 0). By
measuring horizontally or vertically from the center out to
the circle, we can see the radius is 3. Using this information
in our formula gives:
2
2
2
( x − )
0 + ( y − )
0 = 3
simplified a bit, this gives
2
2
x + y = 9
Try it Now
2. Write an equation for a circle centered at (4, -2) with radius 6.
Notice that, relative to a circle centered at the origin, horizontal and vertical shifts of the
circle are revealed in the values of h and k, which are the coordinates for the center of the circle.
Points on a Circle
As noted earlier, an equation for a circle cannot be written so that y is a function of x or vice versa. To find coordinates on the circle given only the x or y value, we must solve
algebraically for the unknown values.
Example 4
Find the points on a circle of radius 5 centered at the origin with an x value of 3.
We begin by writing an equation for the circle centered at the origin with a radius of 5.
2
2
x + y = 25
Substituting in the desired x value of 3 gives an equation we can solve for y
32
2
+ y = 25
2
y = 25 − 9 = 16
y = ± 16 = 4
±
There are two points on the circle with an x value of 3: (3, 4) and (3, -4).
300 Chapter 5
Example 5
Find the x intercepts of a circle with radius 6 centered at the point (2, 4).
We can start by writing an equation for the circle.
( x − )
2 2 + ( y − 4)2 = 36
To find the x intercepts, we need to find the points where y = 0. Substituting in zero for y, we can solve for x.
( x − )
2 2 + (0 − 4)2 = 36
( x − )
2 2 +16 = 36
( x − )
2 2 = 20
x − 2 = ± 20
x = 2 ± 20 = 2 ± 2 5
The x intercepts of the circle are (2 + 2 5,0) and (2 − 2 5 0
, )
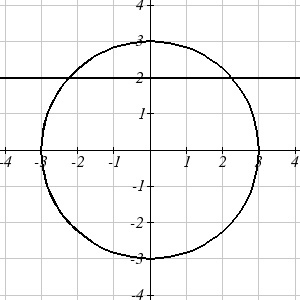
Example 6
In a town, Main Street runs east to west, and Meridian Road runs north to south. A
pizza store is located on Meridian 2 miles south of the intersection of Main and
Meridian. If the store advertises that it delivers within a 3 mile radius, how much of
Main Street do they deliver to?
This type of question is one in which introducing a coordinate system and drawing a
picture can help us solve the problem. We could either place the origin at the
intersection of the two streets, or place the origin at the pizza store itself. It is often
easier to work with circles centered at the origin, so we’ll place the origin at the pizza
store, though either approach would work fine.
Placing the origin at the pizza store, the delivery area
with radius 3 miles can be described as the region inside
the circle described by 2
2
x + y = 9 . Main Street,
located 2 miles north of the pizza store and running east
to west, can be described by the equation y = 2.
To find the portion of Main Street the store will deliver
to, we first find the boundary of their delivery region by
looking for where the delivery circle intersects Main
Street. To find the intersection, we look for the points
on the circle where y = 2. Substituting y = 2 into the
circle equation lets us solve for the corresponding x values.
Section 5.1 Circles 301
2
x + 22 = 9
2
x = 9 − 4 = 5
x = ± 5 ≈ ± 236
.
2
This means the pizza store will deliver 2.236 miles down Main Street east of Meridian
and 2.236 miles down Main Street west of Meridian. We can conclude that the pizza
store delivers to a 4.472 mile segment of Main St.
In addition to finding where a vertical or horizontal line intersects the circle, we can also
find where an arbitrary line intersects a circle.
Example 7
Find where the line f ( x) = 4 x intersects the circle ( x − )
2 2
2
+ y = 16.
Normally, to find an intersection of two functions f(x) and g(x) we would solve for the x value that would make the function equal by solving the equation f(x) = g(x). In the
case of a circle, it isn’t possible to represent the equation as a function, but we can
utilize the same idea. The output value of the line determines the y value:
y = f ( x) = 4 x . We want the y value of the circle to equal the y value of the line, which is the output value of the function. To do this, we can substitute the expression for y
from the line into the circle equation.
( x − )
2 2
2
+ y = 16
we replace y with the line formula: y = 4 x
( x − )
2 2 + (4 x)2 = 16
expand
2
x − 4 x + 4 +16 2
x = 16
and simplify
17 2
x − 4 x + 4 = 16
since this equation is quadratic, we arrange one side to be 0
17 2
x − 4 x −12 = 0
Since this quadratic doesn’t appear to be easily factorable, we can use the quadratic
formula to solve for x:
− (− )
4 ± (− )
4 2 − 17
(
4 )(− )
12
4 ± 832
x =
=
, or approximately x ≈ 0.966 or -0.731
17
(
2 )
34
From these x values we can use either equation to find the corresponding y values.
Since the line equation is easier to evaluate, we might choose to use it:
y = f ( .
0 966) = (
4 .
0
)
966 = 864
.
3
y = f ( 0
−
)
731
.
= 4(−
)
731
.
0
= − 923
.
2
The line intersects the circle at the points (0.966, 3.864) and (-0.731, -2.923).
302 Chapter 5
Try it Now
3. A small radio transmitter broadcasts in a 50 mile radius. If you drive along a straight
line from a city 60 miles north of the transmitter to a second city 70 miles east of the
transmitter, during how much of the drive will you pick up a signal from the
transmitter?
Important Topics of This Section
Distance formula
Equation of a Circle
Finding the x coordinate of a point on the circle given the y coordinate or vice versa
Finding the intersection of a circle and a line
Try it Now Answers
1. 5 5
2. ( x − 4)2 + ( y + )
2 2 = 36
2
2
60
2
x + 60 −
x =
50 gives x = 14 or x = 45.29, corresponding to points (14, 48)and
70
(45.29, 21.18), resulting in a distance of 41.21 miles.
Section 5.1 Circles 303
Section 5.1 Exercises
1. Find the distance between the points (5,3) and (-1,-5).
2. Find the distance between the points (3,3) and (-3,-2).
3. Write an equation of the circle centered at (8 , -10) with radius 8.
4. Write an equation of the circle centered at (-9, 9) with radius 16.
5. Write an equation of the circle centered at (7, -2) that passes through (-10, 0).
6. Write an equation of the circle centered at (3, -7) that passes through (15, 13).
7. Write an equation for a circle where the points (2, 6) and (8, 10) lie along a diameter.
8. Write an equation for a circle where the points (-3, 3) and (5, 7) lie along a diameter.
9. Sketch a graph of ( x − )2 +( y + )2
2
3 = 9 .
10. Sketch a graph of ( x + )2 +( y − )2
1
2 =1 6 .
11. Find the y intercept(s) of the circle with center (2, 3) with radius 3.
12. Find the x intercept(s) of the circle with center (2, 3) with radius 4.
13. At what point in the first quadrant does the line with equation y = 2 x + 5 intersect a circle with radius 3 and center (0, 5)?
14. At what point in the first quadrant does the line with equation y = x + 2 intersect the circle with radius 6 and center (0, 2)?
15. At what point in the second quadrant does the line with equation y = 2 x + 5 intersect a circle with radius 3 and center (-2, 0)?
16. At what point in the first quadrant does the line with equation y = x + 2 intersect the circle with radius 6 and center (-1,0)?
17. A small radio transmitter broadcasts in a 53 mile radius. If you drive along a straight
line from a city 70 miles north of the transmitter to a second city 74 miles east of the
transmitter, during how much of the drive will you pick up a signal from the
transmitter?
18. A small radio t










