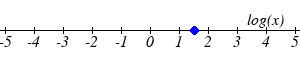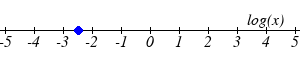130
35
ln
130
t =
≈
68
.
106
− 0123
.
0
It will take about 107 minutes, or one hour and 47 minutes, for the cheesecake to cool.
Of course, if you like your cheesecake served chilled, you’d have to wait a bit longer.
Try it Now
4. A pitcher of water at 40 degrees Fahrenheit is placed into a 70 degree room. One
hour later the temperature has risen to 45 degrees. How long will it take for the
temperature to rise to 60 degrees?
Logarithmic Scales
For quantities that vary greatly in magnitude, a standard scale of measurement is not
always effective, and utilizing logarithms can make the values more manageable. For
example, if the average distances from the sun to the major bodies in our solar system are
listed, you see they vary greatly.
Planet
Distance (millions of km)
Mercury
58
Venus
108
Earth
150
Mars
228
Jupiter
779
Saturn
1430
Uranus
2880
Neptune
4500
Placed on a linear scale – one with equally spaced values – these values get bunched up.
Mercury
Venus Jupiter Saturn
Uranus
Neptune
Earth
Mars
0 500 1000 1500 2000 2500 3000 3500 4000 4500 distance
Section 4.6 Exponential and Logarithmic Models 277
However, computing the logarithm of each value and plotting these new values on a
number line results in a more manageable graph, and makes the relative distances more
apparent. 4
Planet
Distance (millions of km) log(distance)
Mercury
58
1.76
Venus
108
2.03
Earth
150
2.18
Mars
228
2.36
Jupiter
779
2.89
Saturn
1430
3.16
Uranus
2880
3.46
Neptune
4500
3.65
Mercury Venus
Mars Jupiter
Earth
Saturn Uranus Neptune
1.5 1.75 2 2.25 2.5 2.75 3 3.25 3.5 3.75 4 log(distance)
102=100
103=100
104=10000
Sometimes, as shown above, the scale on a logarithmic number line will show the log
values, but more commonly the original values are listed as powers of 10, as shown
below.
A
B
P
C
D
102
103
104
105
106
101
100
10-1
10-2
107
Example 8
Estimate the value of point P on the log scale above
The point P appears to be half way between -2 and -1 in log value, so if V is the value of
this point,
log( V ) ≈ − 5
.
1
Rewriting in exponential form,
V ≈ 10− 5.
1
= 0316
.
0
4 It is interesting to note the large gap between Mars and Jupiter on the log number line.
The asteroid belt, which scientists believe consists of the remnants of an ancient planet, is
located there.
278 Chapter 4
Example 9
Place the number 6000 on a logarithmic scale.
Since log( )
6000 ≈ 8
.
3 , this point would belong on the log scale about here:
6000
102
103
104
105
106
101
100
10-1
10-2
107
Try it Now
5. Plot the data in the table below on a logarithmic scale5 .
Source of Sound/Noise
Approximate Sound Pressure
in µPa (micro Pascals)
Launching of the Space Shuttle
2,000,000,000
Full Symphony Orchestra
2,000,000
Diesel Freight Train at High Speed at 25 m 200,000
Normal Conversation
20,000
Soft Whispering at 2 m in Library
2,000
Unoccupied Broadcast Studio
200
Softest Sound a human can hear
20
Notice that on the log scale above Example 8, the visual distance on the scale between
points A and B and between C and D is the same. When looking at the values these points correspond to, notice B is ten times the value of A , and D is ten times the value of C . A visual linear difference between points corresponds to a relative (ratio) change between the corresponding values.
Logarithms are useful for showing these relative changes. For example, comparing
$1,000,000 to $10,000, the first is 100 times larger than the second.
,1
000
,
000
2
= 100 = 10
000
,
10
Likewise, comparing $1000 to $10, the first is 100 times larger than the second.
000
,1
2
= 100 = 10
10
When one quantity is roughly ten times larger than another, we say it is one order of
magnitude larger. In both cases described above, the first number was two orders of
magnitude larger than the second.
5 From http://www.epd.gov.hk/epd/noise_education/web/ENG_EPD_HTML/m1/intro_5.html, r etrieved Oct 2, 2010
Section 4.6 Exponential and Logarithmic Models 279
Notice that the order of magnitude can be found as the common logarithm of the ratio of
the quantities. On the log scale above, B is one order of magnitude larger than A , and D
is one order of magnitude larger than C .
Orders of Magnitude
Given two values A and B , to determine how many orders of magnitude A is greater than B ,
Difference in orders of magnitude =
A
log
B
Example 10
On the log scale above Example 8, how many orders of magnitude larger is C than B ?
The value B corresponds to 102 = 100
The value C corresponds to 105 =
,
100 000
5
The relative change is
000
,
100
10
3
= 1000 =
= 10 . The log of this value is 3.
2
100
10
C is three orders of magnitude greater than B , which can be seen on the log scale by the
visual difference between the points on the scale.
Try it Now
6. Using the table from Try it Now #5, what is the difference of order of magnitude
between the softest sound a human can hear and the launching of the space shuttle?
An example of a logarithmic scale is the Moment Magnitude Scale (MMS) used for
earthquakes. This scale is commonly and mistakenly called the Richter Scale, which was
a very similar scale succeeded by the MMS.
Moment Magnitude Scale
For an earthquake with seismic moment S , a measurement of earth movement, the
MMS value, or magnitude of the earthquake, is
2
S
M = l
og
3
S 0
Where
16
S = 10 is a baseline measure for the seismic moment.
0
280 Chapter 4
Example 11
If one earthquake has a MMS magnitude of 6.0, and another has a magnitude of 8.0,
how much more powerful (in terms of earth movement) is the second earthquake?
Since the first earthquake has magnitude 6.0, we can find the amount of earth
movement. The value of S 0 is not particularly relevant, so we will not replace it with its
value.
2
S
0
.
6 = log
3
S 0
3
S
0
.
6
= l
og
2
S 0
S
9 = l
og
S 0
S
9
= 10
S 0
9
S = 10 S
0
Doing the same with the second earthquake with a magnitude of 8.0,
2
S
0
.
8 = log
3
S 0
12
S = 10 S
0
From this, we can see that this second value’s earth movement is 1000 times as large as
the first earthquake.
Example 12
One earthquake has magnitude of 3.0. If a second earthquake has twice as much earth
movement as the first earthquake, find the magnitude of the second quake.
Since the first quake has magnitude 3.0,
Section 4.6 Exponential and Logarithmic Models 281
2
.
3 0 = log S
3
S
0
3
.
3 0 = log S
2
S
0
5
.
4 = log S
S
0
.
4 5
10
S
= S 0
.
4 5
S = 10 S 0
Since the second earthquake has twice as much earth movement, for the second quake,
5
.
4
S = 2 ⋅10 S
0
Finding the magnitude,
2
2 ⋅
5
.
4
10 S
M =
0
log
3
S 0
2
M = log(2 ⋅10 5.
4 ) ≈ 201
.
3
3
The second earthquake with twice as much earth movement will have a magnitude of
about 3.2.
In fact, using log properties, we could show that whenever the earth movement doubles,
the magnitude will increase by about 0.201:
2
2 S 2
S
M = log
=
l
og 2 ⋅
3
S
3
S
0
0
2
S
M = log( )
2 + log
3
S 0
2
2
S
M = log( )
2 + l
og
3
3
S 0
2
S
M = 0 201
.
+ l
og
3
S 0
This illustrates the most important feature of a log scale: that multiplying the quantity
being considered will add to the scale value, and vice versa.
282 Chapter 4
Important Topics of this Section
Radioactive decay
Half life
Doubling time
Newton’s law of cooling
Logarithmic Scales
Orders of Magnitude
Moment Magnitude scale
Try it Now Answers
1.
1
r = 10 −1 ≈ − 067
.
0
or 6.7% is the daily rate of decay.
2
2. Less than 230 years, 229.3157 to be exact
3. It will take 10.845 years, or approximately 11 years, for tuition to double.
4. 6.026 hours
5.
Broadcast
Conversation
Softest room Soft
Symphony
Space
Sound
Whisper
Train
Shuttle
105
106
107
108
109
104
103
102
101
1010
9
6. 2 10
x
8
= 10 The sound pressure in µPa created by launching the space shuttle is 8
1
2 10
x
orders of magnitude greater than the sound pressure in µPa created by the softest sound
a human ear can hear.
Section 4.6 Exponential and Logarithmic Models 283
Section 4.6 Exercises
1. You go to the doctor and he injects you with 13 milligrams of radioactive dye. After
12 minutes, 4.75 milligrams of dye remain in your system. To leave the doctor's
office, you must pass through a radiation detector without sounding the alarm. If the
detector will sound the alarm whenever more than 2 milligrams of the dye are in your
system, how long will your visit to the doctor take, assuming you were given the dye
as soon as you arrived and the amount of dye decays exponentially?
2. You take 200 milligrams of a headache medicine, and after 4 hours, 120 milligrams
remain in your system. If the effects of the medicine wear off when less than 80
milligrams remain, when will you need to take a second dose, assuming the amount
of medicine in your system decays exponentially?
3. The half-life of Radium-226 is 1590 years. If a sample initially contains 200 mg,
how many milligrams will remain after 1000 years?
4. The half-life of Fermium-253 is 3 days. If a sample initially contains 100 mg, how
many milligrams will remain after 1 week?
5. The half-life of Erbium-165 is 10.4 hours. After 24 hours a sample still contains 2
mg. What was the initial mass of the sample, and how much will remain after another
3 days?
6. The half-life of Nobelium-259 is 58 minutes. After 3 hours a sample still contains10
mg. What was the initial mass of the sample, and how much will remain after another
8 hours?
7. A scientist begins with 250 grams of a radioactive substance. After 225 minutes, the
sample has decayed to 32 grams. Find the half-life of this substance.
8. A scientist begins with 20 grams of a radioactive substance. After 7 days, the sample
has decayed to 17 grams. Find the half-life of this substance.
9. A wooden artifact from an archeological dig contains 60 percent of the carbon-14 that
is present in living trees. How long ago was the artifact made? (The half-life of
carbon-14 is 5730 years.)
284 Chapter 4
10. A wooden artifact from an archeological dig contains 15 percent of the carbon-14 that
is present in living trees. How long ago was the artifact made? (The half-life of
carbon-14 is 5730 years.)
11. A bacteria culture initially contains 1500 bacteria and doubles in size every half hour.
Find the size of the population after: a) 2 hours b) 100 minutes
12. A bacteria culture initially contains 2000 bacteria and doubles in size every half hour.
Find the size of the population after: a) 3 hours b) 80 minutes
13. The count of bacteria in a culture was 800 after 10 minutes and 1800 after 40
minutes.
a. What was the initial size of the culture?
b. Find the doubling time.
c. Find the population after 105 minutes.
d. When will the population reach 11000?
14. The count of bacteria in a culture was 600 after 20 minutes and 2000 after 35
minutes.
a. What was the initial size of the culture?
b. Find the doubling time.
c. Find the population after 170 minutes.
d. When will the population reach 12000?
15. Find the time required for an investment to double in value if invested in an account
paying 3% compounded quarterly.
16. Find the time required for an investment to double in value if invested in an account
paying 4% compounded monthly
17. The number of crystals that have formed after t hours is given by ( )
0.013
= 20
t
n t
e
.
How long does it take the number of crystals to double?
18. The number of building permits in Pasco t years after 1992 roughly followed the
equation ( )
0.143
= 400
t
n t
e
. What is the doubling time?
Section 4.6 Exponential and Logarithmic Models 285
19. A turkey is pulled from the oven when the internal temperature is 165° Fahrenheit,
and is allowed to cool in a 75° room. If the temperature of the turkey is 145° after
half an hour,
a. What will the temperature be after 50 minutes?
b. How long will it take the turkey to cool to 110°?
20. A cup of coffee is poured at 190° Fahrenheit, and is allowed to cool in a 70° room. If
the temperature of the coffee is 170° after half an hour,
a. What will the temperature be after 70 minutes?
b. How long will it take the coffee to cool to 120°?
21. The population of fish in a farm-stocked lake after t years could be modeled by the
equation P ( t )
1000
=
.
0.6
1+ 9
t
e −
a. Sketch a graph of this equation.
b. What is the initial population of fish?
c. What will the population be after 2 years?
d. How long will it take for the population to reach 900?
22. The number of people in a town who have heard a rumor after t days can be modeled
by the equation N ( t )
500
=
.
0.7
1+ 49
t
e −
a. Sketch a graph of this equation.
b. How many people started the rumor?
c. How many people have heard the rumor after 3 days?
d. How long will it take until 300 people have heard the rumor?
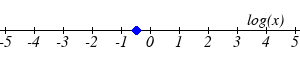
Find the value of the number shown on each logarithmic scale
23.
24.
25.
26.
Plot each set of approximate values on a logarithmic scale.
27. Intensity of sounds: Whisper:
10
−
2
10
W / m , Vacuum:
4
−
Page 1 Page 2 Page 3 Page 4 Page 5 Page 6 Page 7 Page 8 Page 9 Page 10 Page 11 Page 12 Page 13 Page 14 Page 15 Page 16 Page 17 Page 18 Page 19 Page 20 Page 21 Page 22 Page 23 Page 24 Page 25 Page 26 Page 27 Page 28 Page 29 Page 30 Page 31 Page 32 Page 33