10°
65°
b
10
9. A 33-ft ladder leans against a building so that the angle between the ground and the
ladder is 80°. How high does the ladder reach up the side of the building?
10. A 23-ft ladder leans against a building so that the angle between the ground and the
ladder is 80°. How high does the ladder reach up the side of the building?
Section 5.5 Right Triangle Trigonometry 349
11. The angle of elevation to the top of a building in New York is found to be 9 degrees
from the ground at a distance of 1 mile from the base of the building. Using this
information, find the height of the building.
12. The angle of elevation to the top of a building in Seattle is found to be 2 degrees from
the ground at a distance of 2 miles from the base of the building. Using this
information, find the height of the building.
13. A radio tower is located 400 feet from a building. From a window in the building, a
person determines that the angle of elevation to the top of the tower is 36° and that
the angle of depression to the bottom of the tower is 23°. How tall is the tower?
14. A radio tower is located 325 feet from a building. From a window in the building, a
person determines that the angle of elevation to the top of the tower is 43° and that
the angle of depression to the bottom of the tower is 31°. How tall is the tower?
15. A 200 foot tall monument is located in the distance. From a window in a building, a
person determines that the angle of elevation to the top of the monument is 15° and
that the angle of depression to the bottom of the tower is 2°. How far is the person
from the monument?
16. A 400 foot tall monument is located in the distance. From a window in a building, a
person determines that the angle of elevation to the top of the monument is 18° and
that the angle of depression to the bottom of the tower is 3°. How far is the person
from the monument?
17. There is an antenna on the top of a building. From a location 300 feet from the base
of the building, the angle of elevation to the top of the building is measured to be 40°.
From the same location, the angle of elevation to the top of the antenna is measured
to be 43°. Find the height of the antenna.
18. There is lightning rod on the top of a building. From a location 500 feet from the
base of the building, the angle of elevation to the top of the building is measured to be
36°. From the same location, the angle of elevation to the top of the lightning rod is
measured to be 38°. Find the height of the lightning rod.
19. Find the length x.
20. Find the length x.
82
85
63°
39°
36°
50°
x
x
350 Chapter 5
21. Find the length x.
22. Find the length x.
115
119
56°
70°
35°
26°
x
x
23. A plane is flying 2000 feet above sea level
toward a mountain. The pilot observes the top of
the mountain to be 18o above the horizontal, then
immediately flies the plane at an angle of 20o
above horizontal. The airspeed of the plane is
100 mph. After 5 minutes, the plane is directly
above the top of the mountain. How high is the
plane above the top of the mountain (when it passes over)? What is the height of the
mountain? [UW]
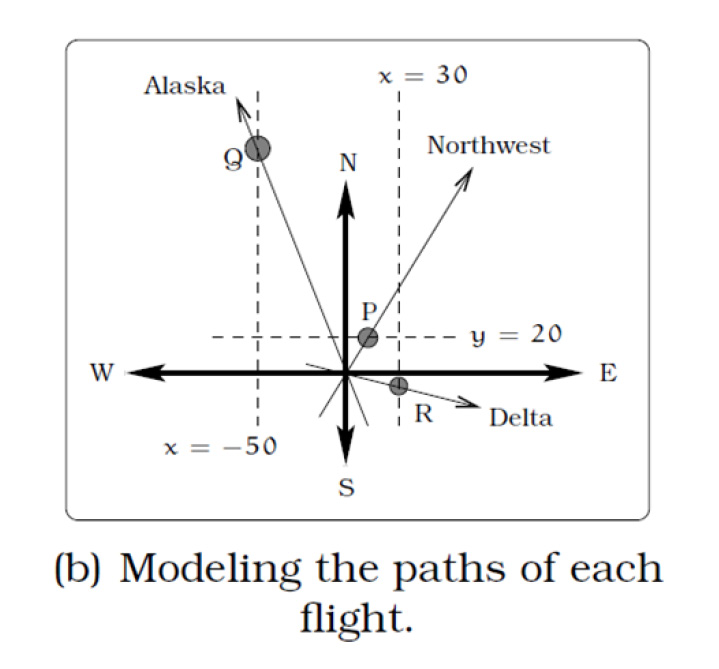
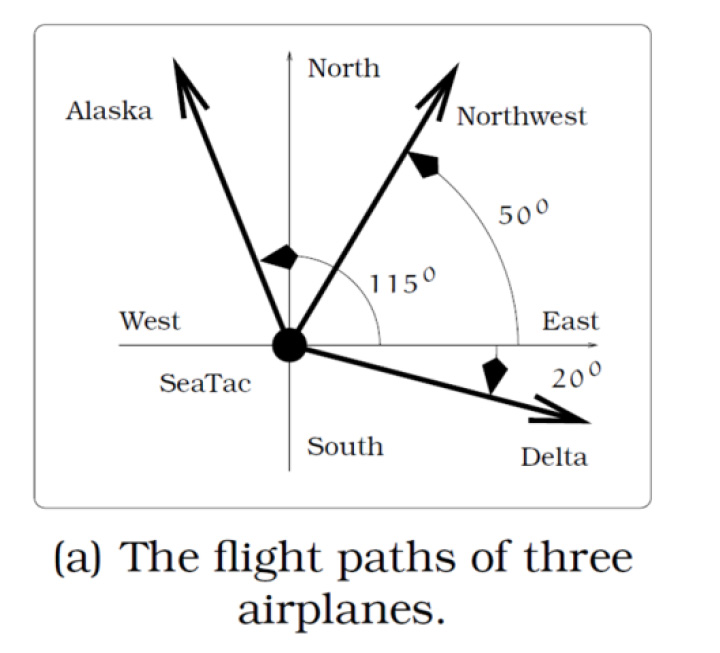
24. Three airplanes depart SeaTac Airport. A Northwest flight is heading in a direction
50° counterclockwise from east, an Alaska flight is heading 115° counterclockwise
from east and a Delta flight is heading 20° clockwise from east. Find the location of
the Northwest flight when it is 20 miles north of SeaTac. Find the location of the
Alaska flight when it is 50 miles west of SeaTac. Find the location of the Delta flight
when it is 30 miles east of SeaTac. [UW]
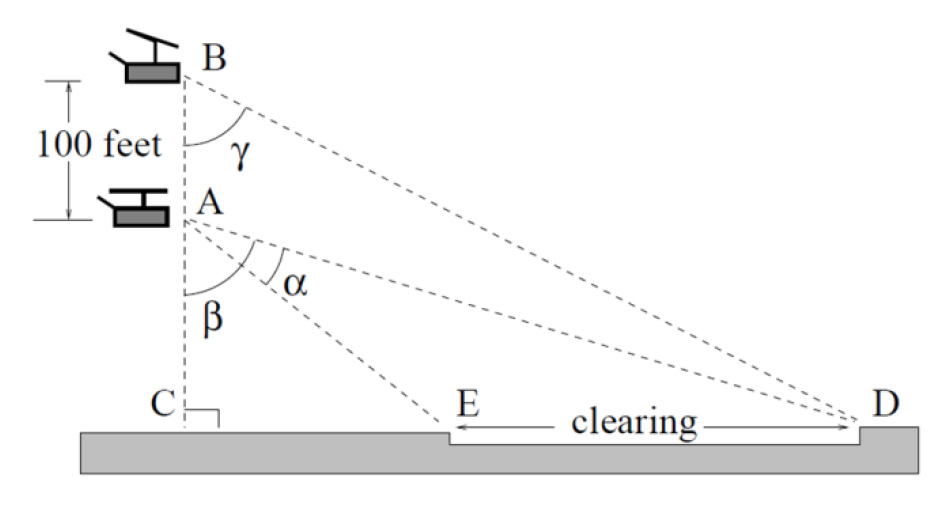
Section 5.5 Right Triangle Trigonometry 351
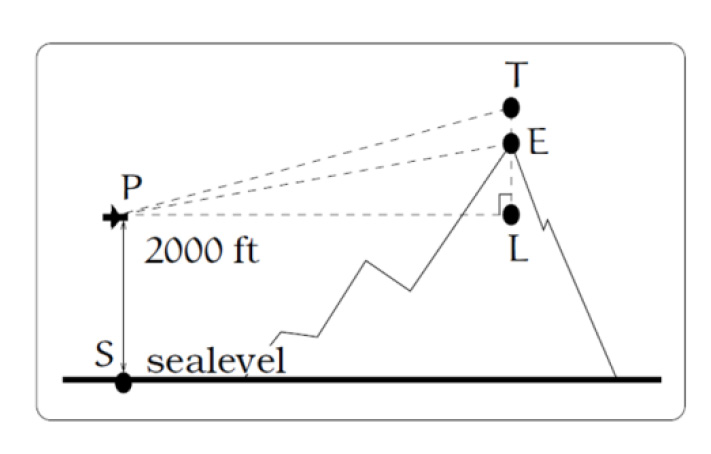
25. The crew of a helicopter needs to
land temporarily in a forest and spot a
flat piece of ground (a clearing in the
forest) as a potential landing site, but
are uncertain whether it is wide
enough. They make two
measurements from A (see picture)
finding α = 25° and β = 54°. They
rise vertically 100 feet to B and
measure γ = 47°. Determine the width of the clearing to the nearest foot. [UW]
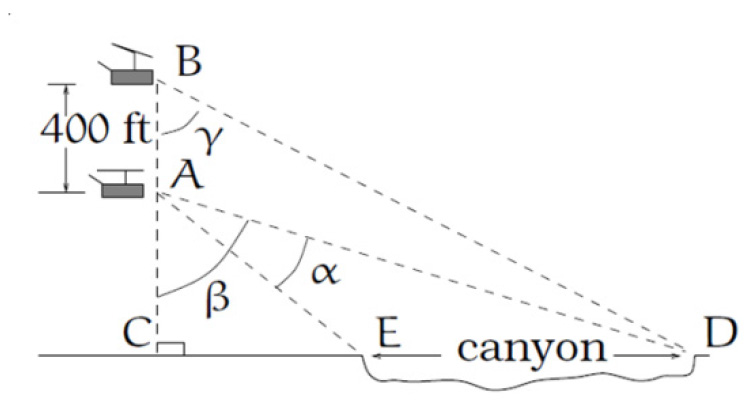
26. A Forest Service helicopter needs to determine
the width of a deep canyon. While hovering,
they measure the angle γ = 48° at position B
(see picture), then descend 400 feet to position
A and make two measurements: α = 13° (the
measure of ∠ EAD), β = 53° (the measure of
∠ CAD). Determine the width of the canyon
to the nearest foot. [UW]
352 Chapter 5

Chapter 6: Periodic Functions
In the previous chapter, the trigonometric functions were introduced as ratios of sides of a
right triangle, and related to points on a circle. We noticed how the x and y values of the points did not change with repeated revolutions around the circle by finding coterminal
angles. In this chapter, we will take a closer look at the important characteristics and
applications of these types of functions, and begin solving equations involving them.
Section 6.1 Sinusoidal Graphs .................................................................................... 353
Section 6.2 Graphs of the Other Trig Functions ......................................................... 369
Section 6.3 Inverse Trig Functions ............................................................................. 379
Section 6.4 Solving Trig Equations ............................................................................ 387
Section 6.5 Modeling with Trigonometric Equations ................................................. 397
Section 6.1 Sinusoidal Graphs
The London Eye1 is a huge Ferris wheel with diameter
135 meters (443 feet) in London, England, which
completes one rotation every 30 minutes. When we
look at the behavior of this Ferris wheel it is clear that it
completes 1 cycle, or 1 revolution, and then repeats this
revolution over and over again.
This is an example of a periodic function, because the
Ferris wheel repeats its revolution or one cycle every 30
minutes, and so we say it has a period of 30 minutes.
In this section, we will work to sketch a graph of a
rider’s height above the ground over time and express
this height as a function of time.
Periodic Functions
A periodic function is a function for which a specific horizontal shift, P, results in the
original function: f ( x + P) = f ( x) for all values of x. When this occurs we call the smallest such horizontal shift with P > 0 the period of the function.
You might immediately guess that there is a connection here to finding points on a circle,
since the height above ground would correspond to the y value of a point on the circle.
We can determine the y value by using the sine function. To get a better sense of this
function’s behavior, we can create a table of values we know, and use them to sketch a
graph of the sine and cosine functions.
1 London Eye photo by authors, 2010, CC-BY
This chapter is part of Precalculus: An Investigation of Functions © Lippman & Rasmussen 2011.
This material is licensed under a Creative Commons CC-BY-SA license.
354 Chapter 6
Listing some of the values for sine and cosine on a unit circle,
θ
0
π
π
π
π
π
2π 3π
5π
6
4
3
2
3
4
6
cos
1
3
1
0
1
-1
2
−
2
−
3
−
2
2
2
2
2
2
sin
0
1
1
0
2
3
3
2
1
2
2
2
2
2
2
Here you can see how for each angle, we use the y value of the point on the circle to
determine the output value of the sine function.
f(θ) = sin( θ)
θ
π π π π
6 4 3 2
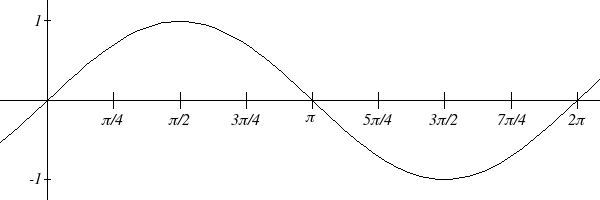
Plotting more points gives the full shape of the sine and cosine functions.
f(θ) = sin( θ)
θ
Notice how the sine values are positive between 0 and π, which correspond to the values
of sine in quadrants 1 and 2 on the unit circle, and the sine values are negative between π
and 2π, corresponding to quadrants 3 and 4.
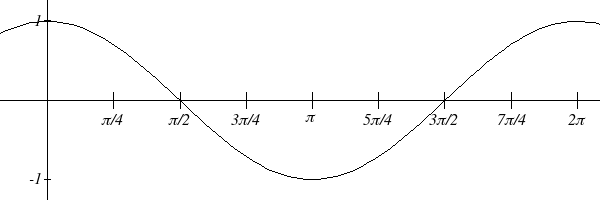
Section 6.1 Sinusoidal Graphs 355
g(θ) = cos( θ)
θ
Like the sine function we can track the value of the cosine function through the 4
quadrants of the unit circle as we place it on a graph.
Both of these functions are defined for all real numbers, since we can evaluate the sine
and cosine of any angle. By thinking of sine and cosine as coordinates of points on a unit
circle, it becomes clear that the range of both functions must be the interval [− ,1 ]
1 .
Domain and Range of Sine and Cosine
The domain of sine and cosine is all real numbers, (−∞,∞) .
The range of sine and cosine is the interval [-1, 1].
Both these graphs are called sinusoidal graphs.
In both graphs, the shape of the graph begins repeating after 2π. Indeed, since any
coterminal angles will have the same sine and cosine values, we could conclude that
sin(θ + 2π ) = sin(θ ) and cos(θ + 2π ) = cos(θ ) .
In other words, if you were to shift either graph horizontally by 2π, the resulting shape
would be identical to the original function. Sinusoidal functions are a specific type of
periodic function.
Period of Sine and Cosine
The periods of the sine and cosine functions are both 2π.
Looking at these functions on a domain centered at the vertical axis helps reveal
symmetries.
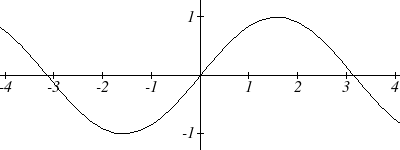

356 Chapter 6
sine
cosine
The sine function is symmetric about the origin, the same symmetry the cubic function
has, making it an odd function. The cosine function is clearly symmetric about the y axis,
the same symmetry as the quadratic function, making it an even function.
Negative Angle Identities
The sine is an odd function, symmetric about the origin, so sin( θ
− ) = −sin(θ ) .
The cosine is an even function, symmetric about the y-axis, so cos( θ
− ) = cos(θ ) .
These identities can be used, among other purposes, for helping with simplification and
proving identities.
π
You may recall the cofunction identity from last chapter;
sin θ
( ) = co
s
−θ .
2
Graphically, this tells us that the sine and cosine graphs are horizontal transformations of
each other. We can prove this by using the cofunction identity and the negative angle
identity for cosine.
π
π
π
π
sin(θ ) = co
s
−θ = co
s −θ + = cos − θ − = co
s θ −
2
2
2
2
Now we can clearly see that if we horizontally shift the cosine function to the right by π/2
we get the sine function.
Remember this shift is not representing the period of the function. It only shows that the
cosine and sine function are transformations of each other.
Example 1 θ−
Simplify sin( ) .
tan(θ )
sin( θ−) Using the even/odd identity
tan(θ )
− sin(θ )
Rewriting the tangent
tan(θ )
Section 6.1 Sinusoidal Graphs 357
− sin(θ )
Inverting and multiplying
sin(θ )cos(θ)
cos(θ )
− sin(θ ) ⋅
Simplifying we get
sin(θ )
− cos(θ )
Transforming Sine and Cosine
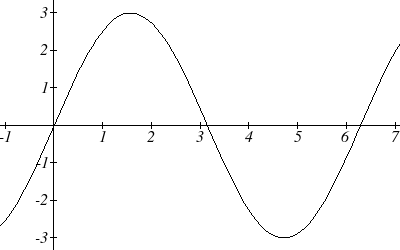
Example 2
A point rotates around a circle of radius 3.
Sketch a graph of the y coordinate of the
point.
Recall that for a point on a circle of radius r,
the y coordinate of the point is y = r sin(θ ) ,
so in this case, we get the
equation y(θ ) = 3sin(θ ) .
The constant 3 causes a vertical stretch of the y values of the function by a factor of 3.
Notice that the period of the function does not change.
Since the outputs of the graph will now oscillate between -3 and 3, we say that the
amplitude of the sine wave is 3.
Try it Now
1. What is the amplitude of the function f (θ ) = 7cos(θ ) ? Sketch a graph of this
function.
Example 3
A circle with radius 3 feet is mounted with its center 4
feet off the ground. The point closest to the ground is
labeled P. Sketch a graph of the height above ground of
3 ft
the point P as the circle is rotated, then find a function
that gives the height in terms of the angle of rotation.
4 ft
P
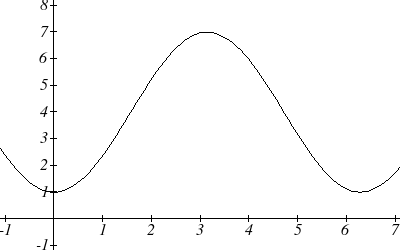
358 Chapter 6
Sketching the height, we note that it will
start 1 foot above the ground, then increase
up to 7 feet above the ground, and continue
to oscillate 3 feet above and below the
center value of 4 feet.
Although we could use a transformation of
either the sine or cosine function, we start by
looking for characteristics that would make
one function easier to use than the other.
We decide to use a cosine function because it starts at the highest or lowest value, while
a sine function starts at the middle value. A standard cosine starts at the highest value,
and this graph starts at the lowest value, so we need to incorporate a vertical reflection.
Second, we see that the graph oscillates 3 above and below the center, while a basic
cosine has an amplitude of one, so this graph has been vertically stretched by 3, as in
the last example.
Finally, to move the center of the circle up to a height of 4, the graph has been vertically
shifted up by 4. Putting these transformations together,
h(θ) = 3−cos(θ)+4
Midline
The center value of a sinusoidal function, the value that the function oscillates above
and below, is called the midline of the function, corresponding to a vertical shift.
The function f(θ) =cos(θ)+ k has midline at y = k.
Try it Now
2. What is the midline of the function f (θ ) = 3cos(θ ) − 4 ? Sketch a graph of the
function.
To answer the Ferris wheel problem at the beginning of the section, we need to be able to
express our sine and cosine functions at inputs of time. To do so, we will utilize
composition. Since the sine function takes an input of an angle, we will look for a
function that takes time as an input and outputs an angle. If we can find a suitable
θ ( t) function, then we can compose this with our f (θ) = cos(θ) function to obtain a
sinusoidal function of time: f ( t) = cos(θ ( t)) .
Section 6.1 Sinusoidal Graphs 359
Example 4
A point completes 1 revolution every 2 minutes around a circle of radius 5. Find the x
coordinate of the point as a function of time, if it starts at (5, 0).
Normally, we would express the x coordinate of a point on a unit circle
using x = r cos(θ ) , here we write the function x(θ ) = 5cos(θ ) .
The rotation rate of 1 revolution every 2 minutes is an angular velocity. We can use this
rate to find a formula for the angle as a function of time. The point begins at an angle
of 0. Since the point rotates 1 revolution
= 2π radians every 2 minutes, it rotates π
x(θ)
radians every minute. After t minutes, it
will have rotated:
θ t() = π t radians
θ
Composing this with the cosine function,
we obtain a function of time.
x( t) = 5cos(θ ( t)) = 5cos(π t)
Notice that this composition has the effect of a horizontal compression, changing the
period of the function.
To see how the period relates to the stretch or compression coefficient B in the equation
f t() = sin( Bt), note that the period will be the time it takes to complete one full
revolution of a circle. If a point takes P minutes to complete 1 revolution, then the
π
π
angular velocity is 2 radians . Then θ t
2
( ) =
t . Composing with a sine function,
P minutes
P
π
2
f t() = sin θ
( t()) = sin
t
P
From this, we can determine the relationship between the coefficient B and the period:
π
B 2
=
. Notice that the stretch or compression coefficient B is a ratio of the “normal
P
period of a sinusoidal function” to the “new period.” If we know the stretch or
π
compression coefficient B, we can solve for the “new period”: P 2
=
.
B
360 Chapter 6
Example 5
π
What is the period of the function
f t() = sin t ?
6
π
Using the relationship above, the stretch/compression factor is B = , so the period
6
π
π
will be
2
2
6
P =
=
= 2π ⋅ = 12.
B
π
π
6
While it is common to compose sine or cosine with functions involving time, the
composition can be done so that the input represents any reasonable quantity.
Example 6
A bicycle wheel with radius 14 inches has the bot

















