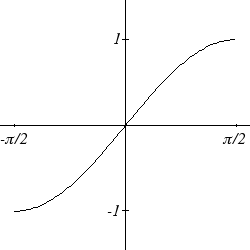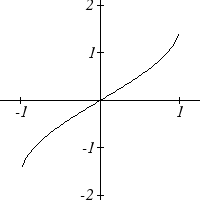Try it Now
2. Given the graph of
π
f (θ ) = 2cos
θ +1 shown, sketch
2
π
the graph of g(θ ) = 2sec
θ +1 on
2
the same axes.
Finally, we’ll look at the graph of cotangent. Based on its definition as the ratio of cosine
to sine, it will be undefined when the sine is zero: at at 0, π, 2π, etc. The resulting graph
is similar to that of the tangent. In fact, it is a horizontal flip and shift of the tangent
function, as we’ll see shortly in Example 3.
1
cos(θ )
f (θ ) = cot(θ ) =
=
tan(θ )
sin(θ )
Features of the Graph of Cotangent
The cotangent graph has period π
Cotangent has domain θ ≠ π
k , where k is an integer
Cotangent has range of all real numbers, (−∞,∞)
In Section 6.1 we determined that the sine function was an odd function and the cosine
was an even function by observing the graph and establishing the negative angle
identities for cosine and sine. Similarly, you may notice from its graph that the tangent
function appears to be odd. We can verify this using the negative angle identities for sine
and cosine: − −
tan(−θ ) sin( θ )
sin(θ )
=
=
= −
cos(
tan
−θ )
cos(θ )
(θ )
The secant, like the cosine it is based on, is an even function, while the cosecant, like the
sine, is an odd function.
374 Chapter 6
Negative Angle Identities Tangent, Cotangent, Secant and Cosecant
tan(−θ ) = − tan(θ )
cot(−θ ) = −cot(θ )
se (c−θ)=se (cθ)
c (
sc −θ ) = −c (
sc θ )
Example 3
π
Prove that tan(θ )
= − cotθ −
2
tan(θ)
Using the definition of tangent
sin(θ )
=
Using the cofunction identities
cos(θ )
π
co
s
−θ
2
=
Using the definition of cotangent
π
sin −θ
2
π
= cot −θ
Factoring a negative from the inside
2
π
= cot− θ −
Using the negative angle identity for cot
2
π
= −cotθ −
2
Important Topics of This Section
The tangent and cotangent functions
Period
Domain
Range
The secant and cosecant functions
Period
Domain
Range
Transformations
Negative Angle identities
Section 6.2 Graphs of the Other Trig Functions 375
Try it Now Answers
1.
2.
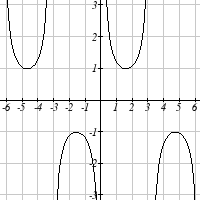
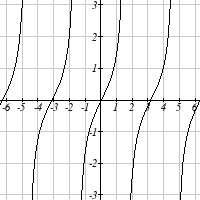
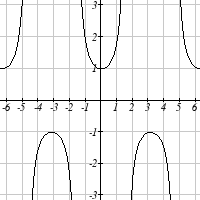
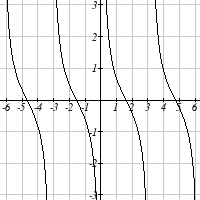
376 Chapter 6
Section 6.2 Exercises
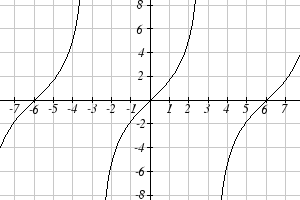
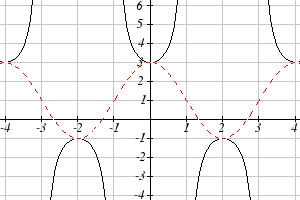
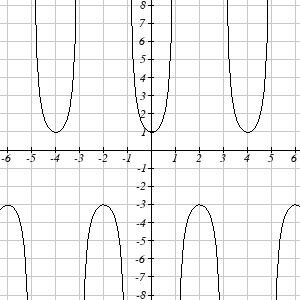
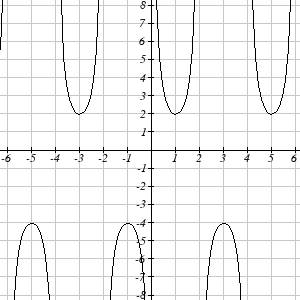
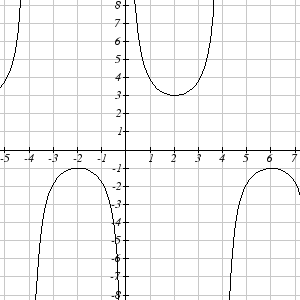
Match each trigonometric function with one of the graphs.
1. f ( x) = tan ( x)
2. f ( x) = se (
c x)
3. f ( x) = csc( x)
4. f ( x) = cot ( x)
I
II
III
IV
Find the period and horizontal shift of each of the following functions.
5. f ( x) = 2 tan (4 x − 32)
6. g ( x) = 3tan (6 x + 42)
π
7. h( x) 2sec
( x )1
=
+
4
π
8. k ( x) = 3sec2 x +
2
π
9. m( x) 6csc
x π
=
+
3
π
π
10. n( x)
5
20
4csc
x
=
−
3
3

Section 6.2 Graphs of the Other Trig Functions 377
11. Sketch a graph of #7 above.
12. Sketch a graph of #8 above.
13. Sketch a graph of #9 above.
14. Sketch a graph of #10 above.
π
15. Sketch a graph of j ( x) tan
x
=
.
2
π
16. Sketch a graph of p( t) 2 tan t
=
−
.
2
Find a formula for each function graphed below.
17.
18.
19.
20.
378 Chapter 6
21. If tan x = 1.5
−
, find tan (− x) .
22. If tan x = 3, find tan (− x) .
23. If sec x = 2, find sec(− x).
24. If sec x = 4
− , find sec(− x).
25. If csc x = 5
− , find csc(− x) .
26. If csc x = 2 , find csc(− x) .
Simplify each of the following expressions completely.
27. cot (− x)cos(− x) + sin (− x)
28. cos(− x) + tan (− x)sin (− x)
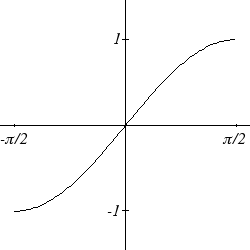
Section 6.3 Inverse Trig Functions 379
Section 6.3 Inverse Trig Functions
In previous sections we have evaluated the trigonometric functions at various angles, but
at times we need to know what angle would yield a specific sine, cosine, or tangent value.
For this, we need inverse functions. Recall that for a one-to-one function, if f ( a) = b , then an inverse function would satisfy f −1 b
( ) = a .
You probably are already recognizing an issue – that the sine, cosine, and tangent
functions are not one-to-one functions. To define an inverse of these functions, we will
need to restrict the domain of these functions to yield a new function that is one-to-one.
We choose a domain for each function that includes the angle zero.
π π
π π
Sine, limited to
− ,
Cosine, limited to [ ,
0 π ]
Tangent, limited to −
,
2 2
2 2
On these restricted domains, we can define the inverse sine, inverse cosine, and inverse
tangent functions.
Inverse Sine, Cosine, and Tangent Functions
π π
For angles in the interval
−1
− , , if sin(θ ) = a , then sin ( a) = θ
2 2
For angles in the interval [ ,
0 π ], if cos(θ ) = a , then
−1
cos ( a) = θ
π π
For angles in the interval
− , , if tan(θ ) = a , then
−1
tan ( a) = θ
2 2
π π
1
sin− ( x) has domain [-1, 1] and range
− ,
2 2
1
cos− ( x) has domain [-1, 1] and range [ ,
0 π ]
π π
1
tan− ( x) has domain of all real numbers and range
− ,
2 2
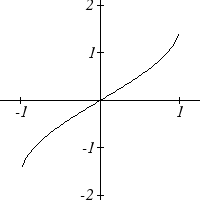

380 Chapter 6
The
1
sin− ( x) is sometimes called the arcsine function, and notated arcsin( a).
The
1
cos− ( x) is sometimes called the arccosine function, and notated arcco (
s a).
The
1
tan− ( x) is sometimes called the arctangent function, and notated arctan( a).
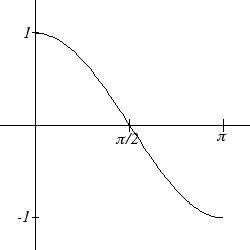
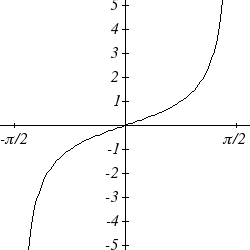
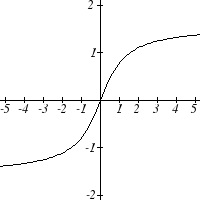
The graphs of the inverse functions are shown here:
1
sin− ( x)
1
cos− ( x)
1
tan− ( x)
Notice that the output of each of these inverse functions is an angle.
Example 1
Evaluate
2
3
a)
− 1
sin 1
b)
−
sin 1 −
c)
−
cos 1 −
d) tan 1−( )
1
2
2
2
a) Evaluating
− 1
sin 1
1
is the same as asking what angle would have a sine value of .
2
2
In other words, what angle θ would satisfy
(θ ) 1
sin
= ? There are multiple angles that
2
π
would satisfy this relationship, such as and 5π , but we know we need the angle in
6
6
π π
−
π
the interval
1
− , , so the answer will be sin 1 = . Remember that the
2 2
2 6
inverse is a function so for each input, we will get exactly one output.
2
b) Evaluating
−
sin 1
5π
7π
−
, we know that
and
both have a sine value of
2
4
4
2
π π
−
, but neither is in the interval
− ,
. For that, we need the negative angle
2
2 2
−
π
coterminal with 7π .
2
sin 1 −
= − .
4
2
4
Section 6.3 Inverse Trig Functions 381
3
c) Evaluating
−
cos 1− , we are looking for an angle in the interval [ ,0π] with a
2
−
π
cosine value of
3
−
. The angle that satisfies this is
3
5
cos 1 −
=
.
2
2 6
π π
d) Evaluating tan 1−( )
1 , we are looking for an angle in the interval
− , with a
2 2
−
π
tangent value of 1. The correct angle is tan 1( )
1 = .
4
Try It Now
1. Evaluate
a) sin 1−(− )
1
b) tan 1−(− )
1
c) cos 1−(− )
1
d)
− 1
cos 1
2
Example 2
Evaluate sin 1−( 97
.
0 ) using your calculator.
Since the output of the inverse function is an angle, your calculator will give you a
degree value if in degree mode, and a radian value if in radian mode.
In radian mode,
1
sin− (0.97) ≈1.3252
In degree mode,
1
sin− (0.97) ≈ 75.93°
Try it Now
2. Evaluate cos 1−(− .
0 4) using your calculator.
In Section 5.5, we worked with trigonometry on a right triangle to solve for the sides of a
triangle given one side and an additional angle. Using the inverse trig functions, we can
solve for the angles of a right triangle given two sides.
Example 3
Solve the triangle for the angle θ.
Since we know the hypotenuse and the side adjacent
12
to the angle, it makes sense for us to use the cosine
θ
function.
9
382 Chapter 6
(θ ) 9
cos
=
Using the definition of the inverse,
12
9
=
−
cos 1
θ
Evaluating
12
θ ≈ 7227
.
0
, or about 41.4096°
There are times when we need to compose a trigonometric function with an inverse
trigonometric function. In these cases, we can find exact values for the resulting
expressions
Example 4
π
−
13
Evaluate sin 1co s
.
6
a) Here, we can directly evaluate the inside of the composition.
13π
3
cos
=
6
2
Now, we can evaluate the inverse function as we did earlier.
−
3 π
sin 1
=
2 3
Try it Now
π
−
11
3. Evaluate cos 1sin−
.
4
Example 5
−1 4
Find an exact value for sincos .
5
Beginning with the inside, we can say there is some angle so
4
=
−
cos 1
θ
, which
5
means
(θ ) 4
cos
= , and we are looking for sin(θ ). We can use the Pythagorean identity
5
to do this.
Section 6.3 Inverse Trig Functions 383
sin2 (θ )+ cos2 (θ ) = 1
Using our known value for cosine
2
2 (θ ) 4
sin
+ = 1
Solving for sine
5
sin2 (θ )
16
= 1−
25
sin(θ )
9
3
= ±
= ±
25
5
Since we know that the inverse cosine always gives an angle on the interval [ ,0π], we
know that the sine of that angle must be positive, so
1
−
4
3
sin cos
=
sin(θ ) =
5
5
Example 6
−1 7
Find an exact value for sintan .
4
While we could use a similar technique as in the last example, we
will demonstrate a different technique here. From the inside, we
7
know there is an angle so
(θ ) 7
tan
= . We can envision this as the
4
opposite and adjacent sides on a right triangle.
θ
Using the Pythagorean Theorem, we can find the hypotenuse of
4
this triangle:
2
2
2
4 + 7 = hypotenuse
hypotenuse = 65
Now, we can evaluate the sine of the angle as opposite side divided by hypotenuse
(θ )
7
sin
=
65
This gives us our desired composition
1
− 7
7
sin tan
=
sin(θ ) =
.
4
65
Try it Now
−1 7
4. Evaluate co ssin .
9
384 Chapter 6
We can also find compositions involving algebraic expressions.
Example 7
−1 x
Find a simplified expression for co ssin , for − 3 ≤ x ≤ 3 .
3
We know there is an angle θ so that sin(θ ) x
= . Using the Pythagorean Theorem,
3
sin2 (θ )+ cos2 (θ ) = 1
Using our known expression for sine
2
x
+ cos2 (θ ) = 1
Solving for cosine