Try it Now Answers
1. Angle of elevation for the cable is 71.69 degrees and the cable is 73.21 m long
π
2. Approximately G( t) 66cos
( t 1)
=
−
+
87
6
404 Chapter 6
Section 6.5 Exercises
In each of the following triangles, solve for the unknown side and angles.
1.
2.
B
B
c
c
3
8
A
A
7
5
3.
4.
B
15
10
7
a
A
A
B
b
12
Find a possible formula for the trigonometric function whose values are in the following
tables.
5. x 0 1 2 3 4 5 6
y -2 4 10 4 -2 4 10
6. x 0 1 2 3 4 5 6
y 1 -3 -7 -3 1 -3 -7
7. Outside temperature over the course of a day can be modeled as a sinusoidal function.
Suppose you know the high temperature for the day is 63 degrees and the low
temperature of 37 degrees occurs at 5 AM. Assuming t is the number of hours since
midnight, find an equation for the temperature, D, in terms of t.
8. Outside temperature over the course of a day can be modeled as a sinusoidal function.
Suppose you know the high temperature for the day is 92 degrees and the low
temperature of 78 degrees occurs at 4 AM. Assuming t is the number of hours since
midnight, find an equation for the temperature, D, in terms of t.
9. A population of rabbits oscillates 25 above and below an average of 129 during the
year, hitting the lowest value in January ( t = 0).
a. Find an equation for the population, P, in terms of the months since January, t.
b. What if the lowest value of the rabbit population occurred in April instead?
Section 6.5 Modeling with Trigonometric Functions 405
10. A population of elk oscillates 150 above and below an average of 720 during the year,
hitting the lowest value in January ( t = 0).
a. Find an equation for the population, P, in terms of the months since January, t.
b. What if the lowest value of the rabbit population occurred in March instead?
11. Outside temperature over the course of a day can be modeled as a sinusoidal function.
Suppose you know the high temperature of 105 degrees occurs at 5 PM and the
average temperature for the day is 85 degrees. Find the temperature, to the nearest
degree, at 9 AM.
12. Outside temperature over the course of a day can be modeled as a sinusoidal function.
Suppose you know the high temperature of 84 degrees occurs at 6 PM and the
average temperature for the day is 70 degrees. Find the temperature, to the nearest
degree, at 7 AM.
13. Outside temperature over the course of a day can be modeled as a sinusoidal function.
Suppose you know the temperature varies between 47 and 63 degrees during the day
and the average daily temperature first occurs at 10 AM. How many hours after
midnight does the temperature first reach 51 degrees?
14. Outside temperature over the course of a day can be modeled as a sinusoidal function.
Suppose you know the temperature varies between 64 and 86 degrees during the day
and the average daily temperature first occurs at 12 AM. How many hours after
midnight does the temperature first reach 70 degrees?
15. A Ferris wheel is 20 meters in diameter and boarded from a platform that is 2 meters
above the ground. The six o'clock position on the Ferris wheel is level with the
loading platform. The wheel completes 1 full revolution in 6 minutes. How many
minutes of the ride are spent higher than 13 meters above the ground?
16. A Ferris wheel is 45 meters in diameter and boarded from a platform that is 1 meter
above the ground. The six o'clock position on the Ferris wheel is level with the
loading platform. The wheel completes 1 full revolution in 10 minutes. How many
minutes of the ride are spent higher than 27 meters above the ground?
17. The sea ice area around the North Pole fluctuates between about 6 million square
kilometers in September to 14 million square kilometers in March. Assuming
sinusoidal fluctuation, during how many months are there less than 9 million square
kilometers of sea ice?
18. The sea ice area around the South Pole fluctuates between about 18 million square
kilometers in September to 3 million square kilometers in March. Assuming
sinusoidal fluctuation, during how many months are there more than 15 million
square kilometers of sea ice?

406 Chapter 6
19. A respiratory ailment called “Cheyne-Stokes Respiration” causes the volume per
breath to increase and decrease in a sinusoidal manner, as a function of time. For one
particular patient with this condition, a machine begins recording a plot of volume per
breath versus time (in seconds). Let b( t) be a function of time t that tells us the volume (in liters) of a breath that starts at time t. During the test, the smallest volume
per breath is 0.6 liters and this first occurs for a breath that starts 5 seconds into the
test. The largest volume per breath is 1.8 liters and this first occurs for a breath
beginning 55 seconds into the test. [UW]
a. Find a formula for the function b( t) whose graph will model the test data for this
patient.
b. If the patient begins a breath every 5 seconds, what are the breath volumes during
the first minute of the test?
20. Suppose the high tide in Seattle occurs at 1:00 a.m. and 1:00 p.m, at which time the
water is 10 feet above the height of low tide. Low tides occur 6 hours after high tides.
Suppose there are two high tides and two low tides every day and the height of the
tide varies sinusoidally. [UW]
a. Find a formula for the function y = h( t) that computes the height of the tide above low tide at time t. (In other words, y = 0 corresponds to low tide.)
b. What is the tide height at 11:00 a.m.?
21. A communications satellite orbits the earth t
miles above the surface. Assume the radius
of the earth is 3,960 miles. The satellite can
only “see” a portion of the earth’s surface,
bounded by what is called a horizon circle.
This leads to a two-dimensional cross-
sectional picture we can use to study the size
of the horizon slice: [UW]
a. Find a formula for α in terms of t.
b. If t = 30,000 miles, what is α? What
percentage of the circumference of the
earth is covered by the satellite? What
would be the minimum number of such
satellites required to cover the circumference?
c. If t = 1,000 miles, what is α? What percentage of the circumference of the earth is
covered by the satellite? What would be the minimum number of such satellites
required to cover the circumference?
d. Suppose you wish to place a satellite into orbit so that 20% of the circumference
is covered by the satellite. What is the required distance t?
Section 6.5 Modeling with Trigonometric Functions 407
22. Tiffany is a model rocket enthusiast. She has been working on a pressurized rocket
filled with nitrous oxide. According to her design, if the atmospheric pressure exerted
on the rocket is less than 10 pounds/sq.in., the nitrous oxide chamber inside the rocket
will explode. Tiff worked from a formula
/10
14.7 h
p
e−
=
pounds/sq.in. for the
atmospheric pressure h miles above sea level. Assume that the rocket is launched at
an angle of α above level ground at sea level with an initial speed of 1400 feet/sec.
Also, assume the height (in feet) of the rocket at time t seconds is given by the
equation y ( t)
2
= 16
− t +1400sin (α ) t . [UW]
a. At what altitude will the rocket explode?
b. If the angle of launch is α = 12°, determine the minimum atmospheric pressure
exerted on the rocket during its flight. Will the rocket explode in midair?
c. If the angle of launch is α = 82°, determine the minimum atmospheric pressure
exerted on the rocket during its flight. Will the rocket explode in midair?
d. Find the largest launch angle α so that the rocket will not explode.
408 Chapter 6
Section 7.1 Solving Trigonometric Equations and Identities 409
Chapter 7: Trigonometric Equations and Identities
In the last two chapters we have used basic definitions and relationships to simplify
trigonometric expressions and solve trigonometric equations. In this chapter we will look
at more complex relationships. By conducting a deeper study of trigonometric identities
we can learn to simplify complicated expressions, allowing us to solve more interesting
applications.
Section 7.1 Solving Trigonometric Equations with Identities .................................... 409
Section 7.2 Addition and Subtraction Identities ......................................................... 417
Section 7.3 Double Angle Identities ........................................................................... 431
Section 7.4 Modeling Changing Amplitude and Midline ........................................... 442
Section 7.1 Solving Trigonometric Equations with Identities
In the last chapter, we solved basic trigonometric equations. In this section, we explore
the techniques needed to solve more complicated trig equations.
Building from what we already know makes this a much easier task.
Consider the function
2
f ( x) = 2 x + x . If you were asked to solve f ( x) = 0, it require simple algebra:
2 2
x + x = 0
Factor
x(2 x + )
1 = 0
Giving solutions
x = 0 or x = 1
−
2
Similarly, for g( t)=sin( t), if we asked you to solve g( t) =0, you can solve this using unit circle values:
sin( t) = 0 for t = ,
0 π , π
2 and so on.
Using these same concepts, we consider the composition of these two functions:
f ( g( t)) = (s
2 in( t))2 + (sin( t)) = 2sin2 ( t) + sin( t)
This creates an equation that is a polynomial trig function. With these types of functions,
we use algebraic techniques like factoring and the quadratic formula, along with
trigonometric identities and techniques, to solve equations.
As a reminder, here are some of the essential trigonometric identities that we have
learned so far:
This chapter is part of Precalculus: An Investigation of Functions © Lippman & Rasmussen 2011.
This material is licensed under a Creative Commons CC-BY-SA license.
410 Chapter 7
Identities
Pythagorean Identities
cos2 ( t) + sin2 ( t) = 1
1+ cot2 ( t) = csc2 ( t)
1+ tan2 ( t) = sec2 ( t)
Negative Angle Identities
sin( t
− ) = −sin( t)
cos( t
− ) = cos( t)
tan( t
− ) = − tan( t)
csc( t
− ) = −csc( t)
sec( t
− ) = sec( t)
cot( t
− ) = −cot( t)
Reciprocal Identities
1
sec( t) =
1
csc( t) =
sin( t)
tan( t) =
1
cot( t) =
cos( t)
sin( t)
cos( t)
tan( t)
Example 1
Solve 2sin2 ( t) + sin( t) = 0 for all solutions with 0 ≤ t < π
2 .
This equation kind of looks like a quadratic equation, but with sin( t) in place of an
algebraic variable (we often call such an equation “quadratic in sine”). As with all
quadratic equations, we can use factoring techniques or the quadratic formula. This
expression factors nicely, so we proceed by factoring out the common factor of sin( t):
sin( t)(2sin( t) + )
1 = 0
Using the zero product theorem, we know that the product on the left will equal zero if
either factor is zero, allowing us to break this equation into two cases:
sin( t) = 0 or
2sin( t) +1 = 0
We can solve each of these equations independently
sin( t) = 0
From our knowledge of special angles
t = 0 or t = π
2sin( t)+1= 0
1
sin( t) = −
Again from our knowledge of special angles
2
7π
t =
or
11π
t =
6
6
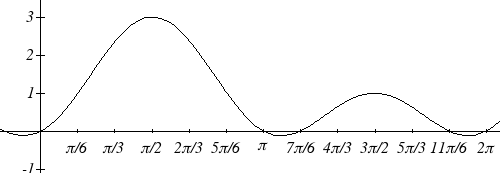
Altogether, this gives us four solutions to the equation on 0≤ t < π2 :
7π 11π
t = ,
0 π ,
,
6
6
We could check these
answers are reasonable by
graphing the function and
comparing the zeros.
Section 7.1 Solving Trigonometric Equations and Identities 411
Example 2
Solve 3sec2 ( t) − 5sec( t) − 2 = 0 for all solutions with 0 ≤ t < π
2 .
Since the left side of this equation is quadratic in secant, we can try to factor it, and
hope it factors nicely.
If it is easier to for you to consider factoring without the trig function present, consider
using a substitution u = sec( t) , resulting in 3 2
u − 5 u − 2 = 0, and then try to factor:
3 2
u − 5 u − 2 = 3
( u + )(
1 u − )
2
Undoing the substitution,
3
( sec( t) + )
1 (sec( t) − )
2 = 0
Since we have a product equal to zero, we break it into the two cases and solve each
separately.
3sec( t)+1=0
Isolate the secant
1
sec( t) = −
Rewrite as a cosine
3
1
1
= −
Invert both sides
cos( t)
3
cos( t) = 3
−
Since the cosine has a range of [-1, 1], the cosine will never take on an output of -3.
There are no solutions to this case.
Continuing with the second case,
sec( t)−2=0
Isolate the secant
sec( t) = 2
Rewrite as a cosine
1 = 2
Invert both sides
cos( t)
1
cos( t) =
This gives two solutions
2
π
t = or
5π
t =
3
3
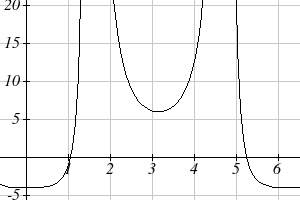
These are the only two solutions on the interval.
By utilizing technology to graph
2
f ( t) = 3sec ( t) − 5sec( t) − 2, a look at a graph
confirms there are only two zeros for this function
on the interval [0, 2π), which assures us that we
didn’t miss anything.
412 Chapter 7
Try it Now
1. Solve 2sin2 ( t) + 3sin( t) +1 = 0 for all solutions with 0 ≤ t < π
2 .
When solving some trigonometric equations, it becomes necessary to first rewrite the
equation using trigonometric identities. One of the most common is the Pythagorean
Identity, sin2 (θ ) + cos2 (θ ) = 1which allows you to rewrite sin2 (θ ) in terms of cos2 (θ )
or vice versa,
2
2
sin (θ ) =1− cos (θ )
2
2
cos (θ ) =1− sin (θ )
This identity becomes very useful whenever an equation involves a combination of sine
and cosine functions.
Example 3
Solve 2sin2 ( t) − cos( t) = 1 for all solutions with 0 ≤ t < π
2 .
Since this equation has a mix of sine and cosine functions, it becomes more complicated
to solve. It is usually easier to work with an equation involving only one trig function.
This is where we can use the Pythagorean Identity.
2sin2 ( t) − cos( t) = 1
Using sin2 (θ ) = 1− cos2 (θ )
2(1− cos2 ( t))− cos( t) = 1
Distributing the 2
2 − 2cos2 ( t) − cos( t) = 1
Since this is now quadratic in cosine, we rearrange the equation so one side is zero and
factor.
− 2cos2 ( t) − cos( t) +1 = 0
Multiply by -1 to simplify the factoring
2cos2 ( t) + cos( t) −1 = 0
Factor
(2cos( t) − )1(cos( t) + )1 = 0
This product will be zero if either factor is zero, so we can break this into two separate
cases and solve each independently.
2cos( t) −1 = 0
or
cos( t) +1 = 0
1
cos( t) =
or
cos( t) = 1
−
2
π
t = or
5π
t =
or
t = π
3
3
Section 7.1 Solving Trigonometric Equations and Identities 413
Try it Now
2. Solve 2sin2 ( t) = 3cos( t) for all solutions with 0 ≤ t < π
2 .
In addition to the Pythagorean Identity, it is often necessary to rewrite the tangent, secant,
cosecant, and cotangent as part of solving an equation.
Example 4
Solve tan( x) = 3sin( x) for all solutions with 0 ≤ x < π
2 .
With a combination of tangent and sine, we might try rewriting tangent
tan( x) = 3sin( x)
sin( x) = 3sin( x)
Multiplying both sides by cosine
cos( x)
sin( x) =3sin( x)cos( x)
At this point, you may be tempted to divide both sides of the equation by sin(x). Resist
the urge. When we divide both sides of an equation by a quantity, we are assuming the
quantity is never zero. In this case, when sin( x) = 0 the equation is satisfied, so we’d
lose those solutions if we divided by the sine.
To avoid this problem, we can rearrange the equation so that one side is zero1.
sin( x) − 3sin( x)cos( x) = 0
Factoring out sin( x) from both parts
sin( x)(1− 3co






