11π
8sin2 x +
6
Try it Now
3. Rewrite − 3 2 sin 5
( x) + 3 2 co 5
s( x) as a single sinusoidal function.
Rewriting a combination of sine and cosine of equal periods as a single sinusoidal
function provides an approach for solving some equations.
Example 7
Solve 3sin(2 x) + 4cos(2 x) = 1 to find two positive solutions.
To approach this, since the sine and cosine have the same period, we can rewrite them
as a single sinusoidal function.
2
A = ( )
3 2 + (4)2 = 25 , so A = 5
3
cos( C) = , so
− 3
C = cos 1
≈ 927
.
0
or C = 2π − 0 927
.
= .
5 356
5
5
Since
4
sin( C) = , a positive value, we need the angle in the first quadrant, C = 0.927.
5
Using this, our equation becomes
5sin(2 x + 927
.
0
) =1
Divide by 5
sin(2 x +
) 1
927
.
0
=
Make the substitution u = 2 x + 0.927
5
Section 7.2 Addition and Subtraction Identities 423
( u) 1
sin
=
The inverse gives a first solution
5
− 1
u = sin 1
≈ 201
.
0
By symmetry, the second solution is
5
u = π − 201
.
0
= 940
.
2
A third solution is
u = 2π + 0 201
.
= 485
.
6
Undoing the substitution, we can find two positive solutions for x.
2 x + 927
.
0
= 201
.
0
or
2 x + .
0 927 = .
2 940 or
2 x + 927
.
0
= 485
.
6
2 x = − 726
.
0
2 x = .
2 013
2 x = 5 558
.
x = .
0
− 363
x = 007
.
1
x = .
2 779
Since the first of these is negative, we eliminate it and keep the two positive solutions,
x = 007
.
1
and x = .
2 779 .
The Product-to-Sum and Sum-to-Product Identities
Identities
The Product-to-Sum Identities
1
sin(α)cos(β ) = (sin(α + β ) + sin(α − β ))
2
1
sin(α)sin(β ) = (cos(α − β ) − cos(α + β ))
21
cos(α)cos(β ) = (cos(α + β ) + cos(α − β ))
2
We will prove the first of these, using the sum and difference of angles identities from the
beginning of the section. The proofs of the other two identities are similar and are left as
an exercise.
Proof of the product-to-sum identity for sin( α)cos( β)
Recall the sum and difference of angles identities from earlier
sin(α + β ) = sin(α)cos(β ) + cos(α)sin(β )
sin(α − β ) = sin(α)cos(β ) − cos(α)sin(β )
Adding these two equations, we obtain
sin(α + β ) + sin(α − β ) = 2sin(α)cos(β )
Dividing by 2, we establish the identity
1
sin(α)cos(β ) = (sin(α + β ) + sin(α − β ))
2
424 Chapter 7
Example 8
Write sin(2 t)sin(4 t) as a sum or difference.
Using the product-to-sum identity for a product of sines
1
sin(2 t)sin(4 t) = (cos(2 t − 4 t) − cos(2 t + 4 t))
2
1
= (cos( 2
− t) − cos(6 t))
If desired, apply the negative angle identity
21
= (cos(2 t) − cos(6 t))
Distribute
21
1
= cos(2 t) − cos(6 t)
2
2
Try it Now
π
π
4. Evaluate
11
co
s
co
s
.
12
12
Identities
The Sum-to-Product Identities
sin( u)+ sin( v)
u + v
u − v
= 2sin
co
s
2
2
sin( u)− sin( v)
u − v
u + v
= 2sin
co
s
2
2
cos( u)+ cos( v)
u + v
u − v
= 2co
s
co
s
2
2
cos( u)− cos( v)
u + v
u − v
= −2sin
sin
2
2
We will again prove one of these and leave the rest as an exercise.
Proof of the sum-to-product identity for sine functions
We begin with the product-to-sum identity
1
sin(α)cos(β ) = (sin(α + β ) + sin(α − β ))
2
We define two new variables:
u = α + β
v = α − β
Section 7.2 Addition and Subtraction Identities 425
Adding these equations yields u + v = α
2 , giving
u + v
α =
2
Subtracting the equations yields u − v = 2β , or
u − v
β =
2
Substituting these expressions into the product-to-sum identity above,
u + v
u − v 1
sin
cos
= (sin( u)+ sin( v)
Multiply by 2 on both sides
2
2 2
u + v
u − v
2sin
cos
= sin( u)+ sin( v)
Establishing the identity
2
2
Example 9
Evaluate co 15
s( )
° − cos(75 )
° .
Using the sum-to-product identity for the difference of cosines,
co 15
s( )
° − cos(75 )
°
15° + °
75 °
15 − °
75
= −2sin
sin
Simplify
2
2
= −2sin( °
45 )sin(− °
30 )
Evaluate
2 −1
2
= 2
− ⋅
⋅
=
2
2
2
Example 10
−
Prove the identity cos(4 t) cos(2 t) = − tan( t) .
sin(4 t) + sin(2 t)
Since the left side seems more complicated, we can start there and simplify.
cos(4 t) − cos(2 t)
Using the sum-to-product identities
sin(4 t) + sin(2 t)
4 t + 2 t
4 t − 2 t
− 2sin
sin
2 2
=
Simplify
4 t + 2 t
4 t − 2 t
2sin
co
s
2
2
− 2sin( t
3 )sin( t)
=
Simplify further
2sin( t
3 )cos( t)
− sin( t)
=
Rewrite as a tangent
cos( t)
= − tan( t)
Establishing the identity
426 Chapter 7
Try it Now
5. Notice that, using the negative angle identity, sin( u)− sin( v) = sin( u) + sin(− v) . Use this along with the sum of sines identity to prove the sum-to-product identity for
sin( u)− sin( v).
Example 11
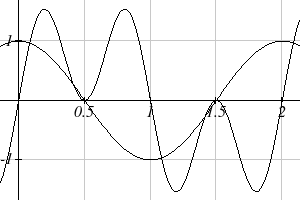
Solve sin (π t) + sin (3π t) = cos(π t) for all solutions with 0 ≤ t < 2.
In an equation like this, it is not immediately obvious how to proceed. One option
would be to combine the two sine functions on the left side of the equation. Another
would be to move the cosine to the left side of the equation, and combine it with one of
the sines. For no particularly good reason, we’ll begin by combining the sines on the
left side of the equation and see how things work out.
sin (π t) + sin (3π t) = cos(π t)
Apply the sum to product identity on the left
π t + 3π t
π t − 3π
2sin
cos
t =
cos(π t) Simplify
2
2
2sin (2π t)cos( π
− t) = cos(π t)
Apply the negative angle identity
2sin (2π t)cos(π t) = cos(π t)
Rearrange the equation to be 0 on one side
2sin (2π t)cos(π t) − cos(π t) = 0
Factor out the cosine
cos(π t)(2sin(2π t) − )
1 = 0
Using the Zero Product Theorem we know that at least one of the two factors must be
π
zero. The first factor, cos(π t) , has period
2
P =
= 2 , so the solution interval of
π
0 ≤ t < 2 represents one full cycle of this function.
cos(π t) = 0
Substitute u = π t
cos( u) = 0
On one cycle, this has solutions
π
u = or
3π
u =
Undo the substitution
2
2
π
π t = , so
1
t =
2
2
3π
π t =
, so
3
t =
2
2
π
The second factor, 2sin (2π t) −1, has period of
2
P =
= 1, so the solution interval
2π
0 ≤ t < 2 contains two complete cycles of this function.
Section 7.2 Addition and Subtraction Identities 427
2sin (2π t) −1 = 0
Isolate the sine
( π t) 1
sin 2
=
u = 2π t
2
1
sin( u) =
On one cycle, this has solutions
2
π
u = or
5π
u =
On the second cycle, the solutions are
6
6
π 13π
π
π
u = 2π + =
or
5
17
u = 2π +
=
Undo the substitution
6
6
6
6
π
2π t = , so
1
t =
6
12
5π
2π t =
, so
5
t =
6
12
13π
2π t =
, so
13
t =
6
12
17π
2π t =
, so
17
t =
6
12
Altogether, we found six solutions on
0 ≤ t < 2, which we can confirm by
looking at the graph.
1 5 1 13 3 17
t =
, , , , ,
12 12 2 12 2 12
Important Topics of This Section
The sum and difference identities
Combining waves of equal periods
Product-to-sum identities
Sum-to-product identities
Completing proofs
Try it Now Answers
cos(α + β ) = cos(α − (−β ))
cos(α)cos(−β ) + sin(α)sin(−β )
1.
cos(α)cos(β ) + sin(α)(−sin(β ))
cos(α)cos(β ) − sin(α)sin(β )
428 Chapter 7
2.
6 − 2
4
π
3.
3
6sin5 x +
4
−
4.
2 − 3
4
5. sin( u) − sin( v)
Use negative angle identity for sine
sin( u) + sin(− v)
Use sum-to-product identity for sine
u + (− v)
u − (− v)
2sin
co
s
2
2
Eliminate the parenthesis
u − v
u + v
2sin
co
s
2
2
Establishing the identity
Section 7.2 Addition and Subtraction Identities 429
Section 7.2 Exercises
Find an exact value for each of the following.
1. sin (75°)
2. sin (195°)
3. cos(165 )
°
4. cos(345 )
°
π
π
π
π
5.
7
cos
6. cos
7.
5
sin
8.
11
sin
12
12
12
12
Rewrite in terms of sin ( x) and cos( x).
π
π
π
π
9.
11
sin x
+
10.
3
sin x −
11.
5
cos x −
12.
2
cos x +
6
4
6
3
Simplify each expression.
π
π
π
π
13. csc
t
−
14. sec
−
w
15. cot
−
x
16. tan
−
x
2
2
2
2
Rewrite the product as a sum.
17. 16sin (16 x)sin (11 x)
18. 20cos(36 t)cos(6 t)
19. 2sin (5 x)cos(3 x)
20. 10cos(5 x)sin (10 x)




