rely on properties that arise from looking at complex numbers from the perspective of
polar coordinates.
We will begin with a review of the definition of complex numbers.
Imaginary Number i
The most basic complex number is i, defined to be i = −1 , commonly called an
imaginary number. Any real multiple of i is also an imaginary number.
Example 1
Simplify − 9 .
We can separate − 9 as 9 −1. We can take the square root of 9, and write the
square root of -1 as i.
− 9 = 9 −1 = i
3
A complex number is the sum of a real number and an imaginary number.
Complex Number
A complex number is a number z = a + bi , where a and b are real numbers a is the real part of the complex number
b is the imaginary part of the complex number
i = −1
Plotting a complex number
We can plot real numbers on a number line. For example, if we wanted to show the
number 3, we plot a point:
Section 8.3 Polar Form of Complex Numbers 481
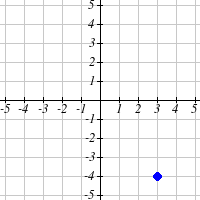
To plot a complex number like 3 − i
4 , we need more than just a number line since there
are two components to the number. To plot this number, we need two number lines,
crossed to form a complex plane.
imaginary
Complex Plane
In the complex plane, the horizontal axis is the real axis
and the vertical axis is the imaginary axis.
real
Example 2
Plot the number 3 − i
4 on the complex plane.
imaginary
The real part of this number is 3, and the imaginary part is -4.
To plot this, we draw a point 3 units to the right of the origin
real
in the horizontal direction and 4 units down in the vertical
direction.
Because this is analogous to the Cartesian coordinate system
for plotting points, we can think about plotting our complex
number z = a + bi as if we were plotting the point ( a, b) in Cartesian coordinates.
Sometimes people write complex numbers as z = x + yi to highlight this relation.
Arithmetic on Complex Numbers
Before we dive into the more complicated uses of complex numbers, let’s make sure we
remember the basic arithmetic involved. To add or subtract complex numbers, we simply
add the like terms, combining the real parts and combining the imaginary parts.
Example 3
Add 3 − i
4 and 2 + i
5 .
Adding 3(−4 i)+(2+5 i), we add the real parts and the imaginary parts
3 + 2 − i
4 + i
5
5 + i
Try it Now
1. Subtract 2 + i
5 from 3 − i
4 .
We can also multiply and divide complex numbers.
482 Chapter 8
Example 4
Multiply: (
4 2 + 5 i) .
To multiply the complex number by a real number, we simply distribute as we would
when multiplying polynomials.
(42+5 i)
= 4 ⋅ 2 + 4 ⋅ i
5
= 8 + i
20
Example 5 +
Divide (2 5 i) .
(4 − i)
To divide two complex numbers, we have to devise a way to write this as a complex
number with a real part and an imaginary part.
We start this process by eliminating the complex number in the denominator. To do
this, we multiply the numerator and denominator by a special complex number so that
the result in the denominator is a real number. The number we need to multiply by is
called the complex conjugate, in which the sign of the imaginary part is changed.
Here, 4+ i is the complex conjugate of 4– i. Of course, obeying our algebraic rules, we
must multiply by 4+ i on both the top and bottom.
(2 + 5 i) (4 + i)
⋅
(4 − i) (4 + i)
To multiply two complex numbers, we expand the product as we would with
polynomials (the process commonly called FOIL – “first outer inner last”). In the
numerator:
(2+5 i)(4+ i)
Expand
2
= 8 + 20 i + 2 i + 5 i
Since i = −1 , 2
i = 1
−
= 8 + 20 i + 2 i + 5( 1)
−
Simplify
= 3+ 22 i
Following the same process to multiply the denominator
(4 − i)(4 + i)
Expand
2
(16 − 4 i + 4 i − i )
Since i = −1 , 2
i = 1
−
(16 − ( 1
− ))
=17
+
Combining this we get 3 22 i
3 22 i
=
+
17
17 17

Section 8.3 Polar Form of Complex Numbers 483
Try it Now
2. Multiply 3 − i
4 and 2 + 3 i .
With the interpretation of complex numbers as points in a plane, which can be related to
the Cartesian coordinate system, you might be starting to guess our next step – to refer to
this point not by its horizontal and vertical components, but using its polar location, given
by the distance from the origin and an angle.
Polar Form of Complex Numbers
Remember, because the complex plane is analogous to the Cartesian plane that we can
think of a complex number z = x + yi as analogous to the Cartesian point ( x, y) and recall how we converted from ( x, y) to polar ( r, θ) coordinates in the last section.
Bringing in all of our old rules we remember the following:
imaginary
x
cos(θ ) =
x = r cos(θ )
r
x + yi
y
sin(θ ) =
y = r sin(θ )
r
r
y
y
tan(θ ) =
2
2
2
x + y = r
θ
real
x
x
With this in mind, we can write z= x+ yi= r cos(θ)+ ir sin(θ).
Example 6
Express the complex number i
4 using polar coordinates.
4 i
On the complex plane, the number 4 i is a distance of 4 from
π
4
π
π
π
2
the origin at an angle of , so
4 i = 4co
s
+ i 4sin
2
2
2
Note that the real part of this complex number is 0.
In the 18th century, Leonhard Euler demonstrated a relationship between exponential and
trigonometric functions that allows the use of complex numbers to greatly simplify some
trigonometric calculations. While the proof is beyond the scope of this class, you will
likely see it in a later calculus class.
484 Chapter 8
Polar Form of a Complex Number and Euler’s Formula
The polar form of a complex number is
iθ
z = re , where Euler’s Formula holds:
θ
rei = r cos(θ ) + ir sin(θ )
Similar to plotting a point in the polar coordinate system we need r and θ to find the
polar form of a complex number.
Example 7
Find the polar form of the complex number -7.
Treating this is a complex number, we can consider the unsimplified version -7+0 i.
Plotted in the complex plane, the number -7 is on the negative horizontal axis, a
distance of 7 from the origin at an angle of π from the positive horizontal axis.
The polar form of the number -7 is iπ
7 e .
Plugging r = 7 and θ = π back into Euler’s formula, we have:
7 eiπ = 7cos(π ) + 7 i sin(π ) = 7
− + 0 i = 7
− as desired.
Example 8
Find the polar form of − 4 + i
4 .
On the complex plane, this complex number would correspond to the point (-4, 4) on a
Cartesian plane. We can find the distance r and angle θ as we did in the last section.
2 2 2
r = x + y
2
2
2
r = (− )
4 + 4
r = 32 = 4 2
To find θ, we can use
x
cos(θ ) =
r
-4+4 i
− 4
2
cos(θ ) =
= −
3π
4 2
2
4 2
4
This is one of known cosine values, and since the point is in
the second quadrant, we can conclude that
3π
θ =
.
4
3π
The polar form of this complex number is
i
4 2 e 4 .
Section 8.3 Polar Form of Complex Numbers 485
Note we could have used
y
tan(θ ) = instead to find the angle, so long as we remember to
x
check the quadrant.
Try it Now
3. Write 3 + i in polar form.
Example 9 π
Write
i
e 6
3 in complex a + bi form.
π
π
π
3 6
e i = 3co
s
+ i 3sin
Evaluate the trig functions
6
6
3
1
= 3⋅
+ i 3⋅
Simplify
2
2
3 3
3
=
+ i
2
2
The polar form of a complex number provides a powerful way to compute powers and
roots of complex numbers by using exponent rules you learned in algebra. To compute a
power of a complex number, we:
1) Convert to polar form
2) Raise to the power, using exponent rules to simplify
3) Convert back to a + bi form, if needed
Example 10
Evaluate (− 4 + i)6
4 .
While we could multiply this number by itself five times, that would be very tedious.
To compute this more efficiently, we can utilize the polar form of the complex number.
3π
In an earlier example, we found that
i
− 4 + i
4 = 4 2 e 4 . Using this,
(−4+ i)6
4
Write the complex number in polar form
6
3
π i
4
= 4 2
m
m
e
Utilize the exponent rule
m
( ab) = a b
π
= (
i
4 2)
6
3
6
4
m n
e
On the second factor, use the rule
mn
( a ) = a
486 Chapter 8
(
π i⋅
= 4 2) 3
6
6
4
e
Simplify
9π i
=
e 2
32768
At this point, we have found the power as a complex number in polar form. If we want
the answer in standard a + bi form, we can utilize Euler’s formula.
9π
9π
9π
32768 2
e i = 32768co
s
+ i 32768sin
2
2
π
Since 9π is coterminal with , we can use our special angle knowledge to evaluate
2
2
the sine and cosine.
9π
9π
32768co
s
+ i 32768sin
=
(
32768 )
0 + i
)
1
(
32768 =
i
32768
2
2
We have found that (− 4 + i
4 )6 =
i
32768 .
The result of the process can be summarized by DeMoivre’s Theorem.
DeMoivre’s Theorem
If z = r (cos(θ ) + i sin(θ )), then for any integer n, n
n
z = r (cos( nθ ) + i sin( nθ ))
We omit the proof, but note we can easily verify it holds in one case using Example 10:
π
π
π
π
( 4
− + i
4 ) = (4 2)6
6
3
cos6 ⋅
+ i
3
9
sin6 ⋅
= 32768 cos
+ i
9
sin
=
i
32768
4
4
2
2
Example 11
Evaluate i
9 .
To evaluate the square root of a complex number, we can first note that the square root
is the same as having an exponent of 1 :
1/ 2
9 i = 9
( i) .
2
To evaluate the power, we first write the complex number in polar form. Since 9 i has
no real part, we know that this value would be plotted along the vertical axis, a distance
π
π
of 9 from the origin at an angle of . This gives the polar form:
i
i
9 = e 2
9
.
2
Section 8.3 Polar Form of Complex Numbers 487
1/ 2
9 i = 9
( i)
Use the polar form
1/ 2
π i
=
2
9
e
Use exponent rules to simplify
1/ 2
π i
1/ 2
2
= 9 e
π 1
1/ 2
i⋅
2 2
= 9 e
Simplify
π i
= e 4
3
Rewrite using Euler’s formula if desired
π
π
= 3co
s
+ i 3sin
Evaluate the sine and cosine
4
4
2
2
= 3
+ i 3
2
2
Using the polar form, we were able to find a square root of a complex number.
i 3 2 3 2
9 =
+
i
2
2
Alternatively, using DeMoivre’s Theorem we can write
1/ 2
π i
π
π
2
9
e
= 3cos
+
i sin and simplify
4
4
Try it Now
4. Write ( + )6
3 i in polar form.
You may remember that equations like 2
x = 4 have two solutions, 2 and -2 in this case,
though the square root 4 only gives one of those solutions. Likewise, the square root
we found in Example 11 is only one of two complex numbers whose square is 9 i.
Similarly, the equation 3
z = 8 would have three solutions where only one is given by the
cube root. In this case, however, only one of those solutions, z = 2, is a real value. To
find the others, we can use the fact that complex numbers have multiple representations
in polar form.
Example 12
Find all complex solutions to 3
z = 8.
488 Chapter 8
Since we are trying to solve 3
z = 8, we can solve for x as
1/3
z = 8 . Certainly one of
these solutions is the basic cube root, giving z = 2. To find others, we can turn to the
polar representation of 8.
Since 8 is a real number, is would sit in the complex plane on the horizontal axis at an
angle of 0, giving the polar form
i
e 0
8 . Taking the 1/3 power of this gives the real
solution:
(8 0 ei)1/3 = 81/3( 0 ei)1/3 = 2 0 e = 2co 0
s( ) + i 2sin(0) = 2
However, since the angle 2π is coterminal with the angle of 0, we could also represent
t