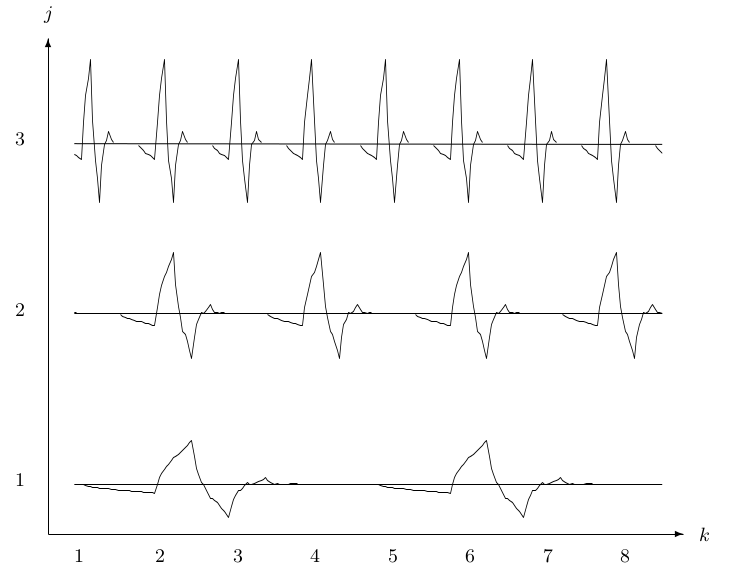
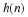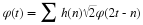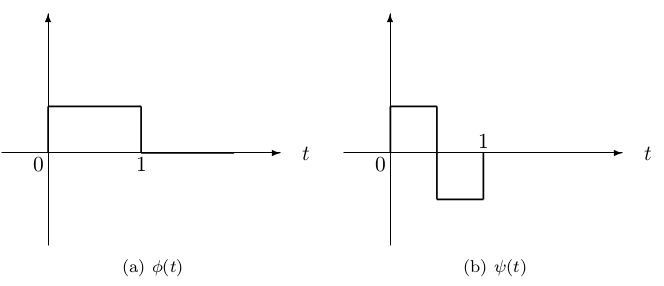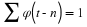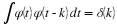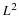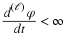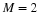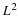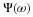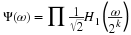11.1. Wavelet-Based Signal Processing
To accomplish frequency domain signal processing, one can take the Fourier
transform (or Fourier series or DFT) of a signal, multiply some of the
Fourier coefficients by zero (or some other constant), then take the
inverse Fourier transform. It is possible to completely remove certain
components of a signal while leaving others completely unchanged. The
same can be done by using wavelet transforms to achieve wavelet-based,
wavelet domain signal processing, or filtering. Indeed, it is sometimes
possible to remove or separate parts of a signal that overlap in both time
and frequency using wavelets, something impossible to do with conventional
Fourier-based techniques.
The classical paradigm for transform-based signal processing is
illustrated in Figure 11.1 where the center “box" could be either a
linear or nonlinear operation. The “dynamics" of the processing are all
contained in the transform and inverse transform operation, which are
linear. The transform-domain processing operation has no dynamics; it is
an algebraic operation. By dynamics, we mean that a process depends on
the present and past, and by algebraic, we mean it depends only on the
present. An FIR (finite impulse response) filter such as is part of a
filter bank is dynamic. Each output depends on the current and a finite
number of past inputs (see Equation 4.11). The process of operating
point-wise on the DWT of a signal is static or algebraic. It does not
depend on the past (or future) values, only the present.
This structure,
which separates the linear, dynamic parts from the nonlinear static parts
of the processing, allows practical and theoretical results that are
impossible or very difficult using a completely general nonlinear dynamic
system.
Linear wavelet-based signal processing consists of the processor block in
Figure 11.1 multiplying the DWT of the signal by some set of
constants (perhaps by zero). If undesired signals or noise can be
separated from the desired signal in the wavelet transform domain, they
can be removed by multiplying their coefficients by zero. This allows a
more powerful and flexible processing or filtering than can be achieved
using Fourier transforms. The result of this total process is a linear,
time-varying processing that is far more versatile than linear,
time-invariant processing. The next section gives an example of using the
concentrating properties of the DWT to allow a faster calculation of the
FFT.
11.2. Approximate FFT using the Discrete Wavelet Transform
In this section, we give an example of wavelet domain signal processing.
Rather than computing the DFT from the time domain signal using the FFT
algorithm, we will first transform the signal into the wavelet domain,
then calculate the FFT, and finally go back to the signal domain which is
now the Fourier domain.
Most methods of approximately calculating the discrete Fourier transform
(DFT) involve calculating only a few output points (pruning), using a
small number of bits to represent the various calculations, or
approximating the kernel, perhaps by using cordic methods. Here we use
the characteristics of the signal being transformed to reduce the amount
of arithmetic. Since the wavelet transform concentrates the energy of
many classes of signals onto a small number of wavelet coefficients, this
can be used to improve the efficiency of the DFT
44, 48, 55, 43 and convolution 45.
The DFT is probably the most important
computational tool in signal processing. Because of the characteristics of
the basis functions, the DFT has
enormous capacity for the improvement of its arithmetic efficiency
15.
The classical Cooley-Tukey fast Fourier transform (FFT) algorithm has the
complexity of 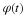 .
Thus the Fourier transform and its fast algorithm, the FFT, are widely
used in many areas, including signal processing and numerical analysis.
Any scheme to speed up the FFT would be very desirable.
.
Thus the Fourier transform and its fast algorithm, the FFT, are widely
used in many areas, including signal processing and numerical analysis.
Any scheme to speed up the FFT would be very desirable.
Although the FFT has been studied extensively, there are still some desired
properties that are not provided by the classical FFT. Here are some of the
disadvantages of the FFT algorithm:
Pruning is not easy.
When the number of input points or output
points are small compared to the length of the DWT, a special technique
called pruning 90 is often used. However,
this often requires that the nonzero input data are grouped
together. Classical FFT pruning algorithms do not work well when the
few nonzero inputs are randomly located. In other words, a sparse signal
may not necessarily give rise to faster algorithm.
No speed versus accuracy tradeoff.
It is common to have a situation where some error would be allowed if
there could be a significant increase in speed.
However, this is not easy with the classical FFT
algorithm. One of the main reasons is that the twiddle factors in
the butterfly operations are unit magnitude complex numbers. So
all parts of the FFT structure are of equal importance. It is hard to
decide which part of the FFT structure to omit when error is allowed and
the speed is crucial. In other words, the FFT is a single speed and single
accuracy algorithm.
No built-in noise reduction capacity.
Many real world signals are noisy. What people are really interested in
are the DFT of the signals without the noise. The classical FFT algorithm
does not have built-in noise reduction capacity. Even if other denoising
algorithms are used, the FFT requires the same computational complexity
on the denoised signal. Due to the above mentioned shortcomings, the fact
that the signal has been denoised cannot be easily used to speed up the
FFT.
Review of the Discrete Fourier Transform and FFT
The discrete Fourier transform (DFT) is defined for a length-N
complex data sequence by
where we use 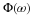 .
There are several ways to derive the different fast Fourier transform (FFT)
algorithms. It can be done by using index mapping 15, by
matrix factorization, or by polynomial factorization. In this chapter, we
only discuss the matrix factorization approach, and only discuss the so-called
radix-2 decimation in time (DIT) variant of the FFT.
.
There are several ways to derive the different fast Fourier transform (FFT)
algorithms. It can be done by using index mapping 15, by
matrix factorization, or by polynomial factorization. In this chapter, we
only discuss the matrix factorization approach, and only discuss the so-called
radix-2 decimation in time (DIT) variant of the FFT.
Instead of repeating the derivation of the FFT algorithm, we show the
block diagram and matrix factorization, in an effort to highlight the basic
idea and gain some insight. The block diagram of the last stage of a length-8
radix-2 DIT FFT is shown in Figure 11.2. First, the input data are
separated into even and odd groups. Then, each group goes through a
length-4 DFT block. Finally, butterfly operations are used to
combine the shorter DFTs into longer DFTs.
The details of the butterfly operations are shown in
Figure 11.3, where WNi=e–j2πi/N is called
the twiddle factor. All the twiddle factors are of magnitude one
on the unit circle. This is the main reason that there is no
complexity versus accuracy tradeoff for the classical FFT. Suppose some of
the twiddle factors had very small magnitude,
then the corresponding
branches of the butterfly operations could be dropped (pruned) to reduce
complexity while minimizing the error to be introduced. Of course the error
also depends on the value of the data to be multiplied with the twiddle
factors. When the value of the data is unknown, the best way is
to cutoff the branches with small twiddle factors.
The computational complexity of the FFT algorithm can be easily
established. If we let CFFT(N) be the complexity for a length-N FFT, we
can show
(11.2)
CFFT
(
N
)
=
O
(
N
)
+
2
CFFT
(
N
/
2
)
,
where O(N) denotes linear complexity. The solution to
Equation Equation 11.2 is well known:
This is a classical case where the divide and conquer approach results
in very effective solution.
The matrix point of view gives us additional insight. Let FN be
the 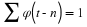 DFT matrix; i.e., FN(m,n)=e–j2πmn/N,
where
DFT matrix; i.e., FN(m,n)=e–j2πmn/N,
where 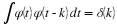 . Let SN be
the
. Let SN be
the 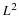 even-odd separation matrix; e.g.,
even-odd separation matrix; e.g.,
Clearly SN'SN=IN, where IN is the
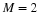 identity matrix. Then the DIT FFT is based on the following matrix
factorization,
identity matrix. Then the DIT FFT is based on the following matrix
factorization,
where TN/2 is a diagonal matrix with WNi,
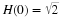 on the diagonal. We can visualize the
above factorization as
on the diagonal. We can visualize the
above factorization as
where we image the real part of DFT matrices, and the magnitude of the
matrices for butterfly operations and even-odd separations. N is taken to
be 128 here.
Review of the Discrete Wavelet Transform
In this section, we briefly review the fundamentals of the discrete wavelet
transform and introduce the necessary notation for future sections. The
details of the DWT have been covered in other chapters.
At the heart of the discrete wavelet transform are a pair of filters
h and g — lowpass and highpass respectively. They have to
satisfy a set of constraints Figure: Sinc Scaling Function and Wavelet 110, 99, 108.
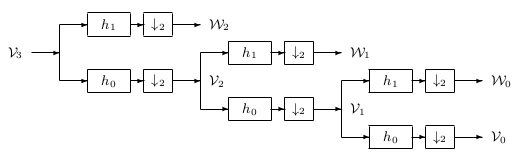
The block diagram of the DWT is shown in Figure 11.4. The input
data are first filtered by h and g then downsampled. The same
building block is further iterated on the lowpass outputs.
The computational complexity of the DWT algorithm can also be easily
established. Let CDWT(N) be the complexity for a length-N DWT. Since
after each scale, we only further operate on half of the output data, we
can show
(11.7)
CDWT
(
N
)
=
O
(
N
)
+
CDWT
(
N
/
2
)
,
which gives rise to the solution
(11.8)
CDWT
(
N
)
=
O
(
N
)
.
The operation in Figure 11.4 can also be expressed in matrix
form WN; e.g., for Haar wavelet,
The orthogonality conditions on h and g ensure WN'WN=IN. The matrix for multiscale DWT is formed by
WN for different N; e.g., for three scale DWT,
We could further iterate the building block on some of the highpass
outputs. This generalization is called the wavelet packets
25.
The Algorithm Development
The key to the fast Fourier transform is the factorization of FN
into several sparse matrices, and one of the sparse matrices represents two DFTs
of half the length. In a manner similar to the DIT FFT, the following matrix
factorization can be made:
where AN/2,BN/2,CN/2, and
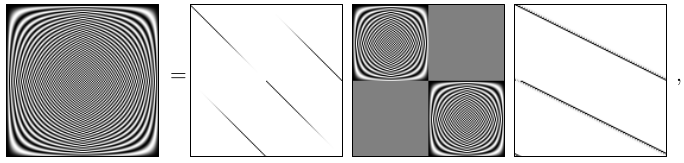
DN/2 are all diagonal matrices. The values on the diagonal of
AN/2 and CN/2 are the length-N DFT (i.e.,
frequency response) of h,
and the values on the diagonal of BN/2 and DN/2
are the length-N DFT of g. We can visualize the
above factorization as
where we image the real part of DFT matrices, and the magnitude of the
matrices for butterfly operations and the one-scale DWT using length-16
Daubechies' wavelets 26, 27. Clearly we
can see that the new twiddle factors have non-unit magnitudes.
The above factorization suggests a DWT-based FFT algorithm. The
block diagram of the last stage of a length-8 algorithm is shown in
Figure 11.5. This scheme is
iteratively applied to shorter length DFTs to get the full DWT based FFT
algorithm. The final system is equivalent to a full binary tree wavelet
packet transform 24 followe