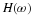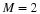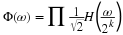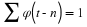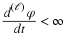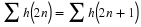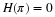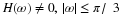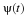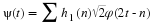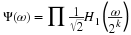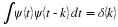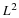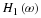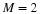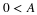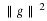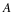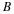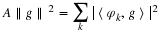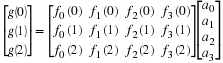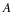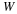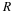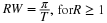10.1. Finite Wavelet Expansions and Transforms
The wavelet expansion of a signal f(t) as first formulated in Section 2.2
is repeated here by
where the 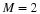 form a basis or tight frame for the signal
space of interest (e.g., L2). At first glance, this infinite series
expansion seems to have the same practical problems in calculation that an
infinite Fourier series or the Shannon sampling formula has. In a
practical situation, this wavelet expansion, where the coefficients are
called the discrete wavelet transform (DWT), is often more easily
calculated. Both the time summation over the index k and the scale
summation over the index j can be made finite with little or no error.
form a basis or tight frame for the signal
space of interest (e.g., L2). At first glance, this infinite series
expansion seems to have the same practical problems in calculation that an
infinite Fourier series or the Shannon sampling formula has. In a
practical situation, this wavelet expansion, where the coefficients are
called the discrete wavelet transform (DWT), is often more easily
calculated. Both the time summation over the index k and the scale
summation over the index j can be made finite with little or no error.
The Shannon sampling expansion 8, 6 of a signal with
infinite support in terms of sinc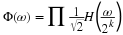 expansion
functions
expansion
functions
requires an infinite sum to evaluate f(t) at one point because the sinc
basis functions have infinite support. This is not necessarily true for a
wavelet expansion where it is possible for the wavelet basis functions to
have finite support and, therefore, only require a finite summation over
k in Equation 10.1 to evaluate f(t) at any point.
The lower limit on scale j in Equation 10.1 can be made finite by adding the
scaling function to the basis set as was done in Equation 3.28. By using the
scaling function, the expansion in Equation 10.1 becomes
where j=J0 is the coarsest scale that is separately represented. The
level of resolution or coarseness to start the expansion with is arbitrary,
as was shown in Chapter: A multiresolution formulation of Wavelet Systems in Equation 3.19, Equation 3.20, and
Equation 3.21. The space spanned by the scaling function contains all the
spaces spanned by the lower resolution wavelets from j=–∞ up to the
arbitrary starting point j=J0. This means VJ0=W–∞⊕⋯⊕WJ0–1. In a practical case,
this would be the scale where separating detail becomes important. For a
signal with finite support (or one with very concentrated energy), the
scaling function might be chosen so that the support of the scaling
function and the size of the features of interest in the signal being
analyzed were approximately the same.
This choice is similar to the choice of period for the basis sinusoids in
a Fourier series expansion. If the period of the basis functions is
chosen much larger than the signal, much of the transform is used to
describe the zero extensions of the signal or the edge effects.
The choice of a finite upper limit for the scale j in Equation 10.1 is more
complicated and usually involves some approximation. Indeed, for
samples of f(t) to be an accurate description of the signal, the signal
should be essentially bandlimited and the samples taken at least at the
Nyquist rate (two times the highest frequency in the signal's Fourier
transform).
The question of how one can calculate the Fourier series coefficients of a
continuous signal from the discrete Fourier transform of samples of the
signal is similar to asking how one calculates the discrete wavelet
transform from samples of the signal. And the answer is similar. The
samples must be “dense" enough. For the Fourier series, if a frequency
can be found above which there is very little energy in the signal (above
which the Fourier coefficients are very small), that determines the
Nyquist frequency and the necessary sampling rate. For the wavelet
expansion, a scale must be found above which there is negligible detail or
energy. If this scale is j=J1, the signal can be written
or, in terms of wavelets, Equation 10.3 becomes
This assumes that approximately f∈VJ1 or equivalently,
∥f–PJ1f∥≈0, where PJ1 denotes the orthogonal
projection of f onto VJ1.
Given f(t)∈VJ1 so that the expansion in Equation 10.5
is exact, one computes the DWT coefficients in two steps.
Projection onto finest scale: Compute 〈f,φJ1,k〉
Analysis: Compute 〈f,ψj,k〉,
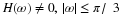 and 〈f,φJ0,k〉.
and 〈f,φJ0,k〉.
For J1 large enough, φJ1,k(t) can be approximated by a
Dirac impulse at its center of mass since 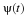 . For large j this gives
. For large j this gives
where 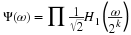 is the first moment of
φ(t). Therefore the scaling function coefficients at the j=J1
scale are
is the first moment of
φ(t). Therefore the scaling function coefficients at the j=J1
scale are
which are approximately
For all 2-regular wavelets (i.e., wavelets with two vanishing moments,
regular wavelets other than the Haar wavelets—even in the M-band case
where one replaces 2 by M in the above equations, m0=0), one can
show that the samples of the functions themselves form a third-order
approximation to the scaling function coefficients of the signal
2. That is, if f(t) is a quadratic polynomial, then
Thus, in practice, the finest scale J1 is determined by the sampling
rate. By rescaling the function and amplifying it appropriately, one
can assume the samples of f(t) are equal to the scaling function
coefficients. These approximations are made better by setting some of
the scaling function moments to zero as in the coiflets. These are
discussed in Section: Approximation of Scaling Coefficients by Samples of the Signal .
Finally there is one other aspect to consider. If the signal has finite
support and L samples are given, then we have L nonzero
coefficients 〈f,φJ1,k〉. However, the DWT will
typically have more than L coefficients since the wavelet and scaling
functions are obtained by convolution and downsampling. In other words,
the DWT of a L-point signal will have more than L points. Considered
as a finite discrete transform of one vector into another, this situation
is undesirable. The reason this “expansion" in dimension occurs is that
one is using a basis for L2 to represent a signal that is of finite
duration, say in L2[0,P].
When calculating the DWT of a long signal, J0 is usually chosen to give
the wavelet description of the slowly changing or longer duration features
of the signal. When the signal has finite support or is periodic, J0
is generally chosen so there is a single scaling coefficient for the
entire signal or for one period of the signal. To reconcile the
difference in length of the samples of a finite support signal and the
number of DWT coefficients, zeros can be appended to the samples of f(t)
or the signal can be made periodic as is done for the DFT.
10.2. Periodic or Cyclic Discrete Wavelet Transform
If f(t) has finite support, create a periodic version of it by
where the period P is an integer. In this case, 〈f,φj,k〉 and 〈f,ψj,k〉 are periodic
sequences in k with period 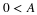 (if j≥0 and 1 if j<0) and
(if j≥0 and 1 if j<0) and
where 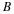 (k modulo
(k modulo 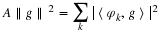 ) and
) and  . An obvious choice for J0 is 1. Notice that
in this case given L=2J1 samples of the signal, 〈f,φJ1,k〉, the wavelet transform has exactly
1+1+2+22+⋯+2J1–1=2J1=L terms. Indeed, this gives a
linear, invertible discrete transform which can be considered apart from
any underlying continuous process similar the discrete Fourier transform
existing apart from the Fourier transform or series.
. An obvious choice for J0 is 1. Notice that
in this case given L=2J1 samples of the signal, 〈f,φJ1,k〉, the wavelet transform has exactly
1+1+2+22+⋯+2J1–1=2J1=L terms. Indeed, this gives a
linear, invertible discrete transform which can be considered apart from
any underlying continuous process similar the discrete Fourier transform
existing apart from the Fourier transform or series.
There are at least three ways to calculate this cyclic DWT and they are
based on the equations Equation 10.25, Equation 10.26, and Equation 10.27 later
in this chapter. The first method simply convolves the scaling
coefficients at one scale with the time-reversed coefficients h(–n) to
give an L+N–1 length sequence. This is aliased or wrapped as indicated
in Equation 10.27 and programmed in dwt5.m in Appendix 3.
The second method creates a periodic  by
concatenating an appropriate number of cj(k) sections together then
convolving h(n) with it. That is illustrated in Equation 10.25 and in
by
concatenating an appropriate number of cj(k) sections together then
convolving h(n) with it. That is illustrated in Equation 10.25 and in
dwt.m in Appendix 3. The third approach constructs a periodic
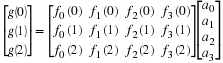 and convolves it with cj(k) to implement Equation 10.26.
The Matlab programs should be studied to understand how these ideas
are actually implemented.
and convolves it with cj(k) to implement Equation 10.26.
The Matlab programs should be studied to understand how these ideas
are actually implemented.
Because the DWT is not shift-invariant, different implementations of the
DWT may appear to give different results because of shifts of the signal
and/or basis functions. It is interesting to take a test signal and
compare the DWT of it with different circular shifts of the signal.
Making f(t) periodic can introduce discontinuities at 0 and P. To
avoid this, there are several alternative constructions of orthonormal
bases for L2[0,P]1, 4, 5, 3. All of these
constructions use (directly or indirectly) the concept of time-varying
filter banks. The basic idea in all these constructions is to retain basis
functions with support in [0,P], remove ones with support outside
[0,P] and replace the basis functions that overlap across the endpoints
with special entry/exit functions that ensure completeness.
These boundary functions are chosen so that the constructed basis is
orthonormal. This is discussed in Section: Time-Varying Filter Bank Trees . Another way to
deal with edges or boundaries uses “lifting" as mentioned in
Section: Lattices and Lifting.
10.3. Filter Bank Structures for Calculation of the DWT and Complexity
Given that the wavelet analysis of a signal has been posed in terms of the
finite expansion of Equation 10.5, the discrete wavelet transform (expansion
coefficients) can be calculated using Mallat's algorithm implemented by a
filter bank as described in Chapter: Filter Banks and the Discrete Wavelet Transform and expanded upon in
Chapter: Filter Banks and Transmultiplexers . Using the direct calculations described by the
one-sided tree structure of filters and down-samplers in Figure: Three-Stage Two-Band Analysis Tree
allows a simple determination of the computational complexity.
If we assume the length of the sequence of the signal is L and the
length of the sequence of scaling filter coefficients h(n) is N, then
the number of multiplications necessary to calculate each scaling function
and wavelet expansion coefficient at the next scale, 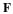 and
and
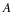 , from the samples of the signal,
, from the samples of the signal, 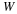 , is
LN. Because of the downsampling,
only half are needed to calculate the
coefficients at the next lower scale,
, is
LN. Because of the downsampling,
only half are needed to calculate the
coefficients at the next lower scale, 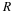 and
and 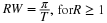 , and
repeats until there is only one coefficient at a scale of j=J0. The
total number of multiplications is, therefore,
, and
repeats until there is only one coefficient at a scale of j=J0. The
total number of multiplications is, therefore,
(10.14)
=
L
N
(
1
+
1
/
2
+
1
/
4
+
⋯
+
1
/
L
)
=
2
N
L
–
N
which is linear in L and in N. The nu