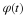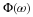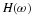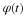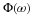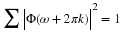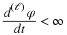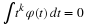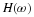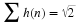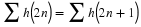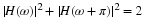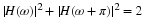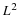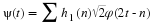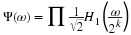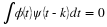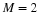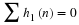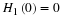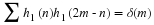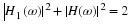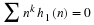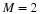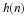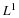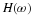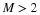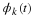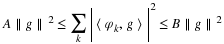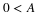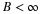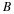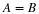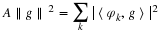This appendix contains outline proofs and derivations for the theorems and formulas given in early part of Chapter: The Scaling Function and Scaling Coefficients, Wavelet and Wavelet Coefficients . They are not intended to be complete or formal, but they should be sufficient to understand the ideas behind why a result is true and to give some insight into its interpretation as well as to indicate assumptions and restrictions.

Proof 1 The conditions given by Equation 6.10 and Equation 8.7 can be derived by integrating both sides of

(13.1)

and making the change of variables y=Mx

(13.2)

and noting the integral is independent of translation which gives

(13.3)

With no further requirements other than φ∈L¹ to allow the sum and integral interchange and 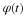, this gives Equation 8.7 as

(13.4)

and for M=2 gives Equation 6.10. Note this does not assume orthogonality nor any specific normalization of φ(t) and does not even assume M is an integer.

This is the most basic necessary condition for the existence of φ(t) and it has the fewest assumptions or restrictions.

Proof 2 The conditions in Equation 6.14 and Equation 8.8 are a down-sampled orthogonality of translates by M of the coefficients which results from the orthogonality of translates of the scaling function given by

(13.5)

in ???. The basic scaling equation Equation 13.1 is substituted for both functions in Equation 13.5 giving

(13.6)

which, after reordering and a change of variable 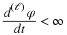, gives

(13.7)

Using the orthogonality in Equation 13.5 gives our result

(13.8)

in Equation 6.13 and Equation 8.8. This result requires the orthogonality condition Equation 13.5, M must be an integer, and any non-zero normalization E may be used.

Proof 3 (Corollary 2) The result that

(13.9)

in Equation 6.17 or, more generally

(13.10)

is obtained by breaking Equation 13.4 for M=2 into the sum of the even and odd coefficients.

(13.11)

Next we use Equation 13.8 and sum over n to give

(13.12)

which we then split into even and odd sums and reorder to give:

Solving Equation 13.11 and Equation 13.13 simultaneously gives 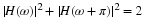and our result Equation 6.17 or Equation 13.9 for M=2.

If the same approach is taken with Equation 8.7 and Equation 8.8 for M=3, we have

(13.14)

which, in terms of the partial sums K_i, is

(13.15)

Using the orthogonality condition Equation 13.13 as was done in Equation 13.12 and ??? gives

Equation Equation 13.15 and Equation 13.16 are simultaneously true if and only if . This process is valid for any integer M and any non-zero normalization.

Proof 3 If the support of φ(x) is [0,N–1], from the basic recursion equation with support of h(n) assumed as 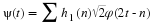we have

(13.17)

where the support of the right hand side of Equation 13.17 is 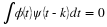. Since the support of both sides of Equation 13.17 must be the same, the limits on the sum, or, the limits on the indices of the non zero h(n) are such that N₁=0 and N₂=N, therefore, the support of h(n) is [0,N–1].

Proof 4 First define the autocorrelation function

(13.18)

and the power spectrum

(13.19)

which after changing variables, y=x–t, and reordering operations gives

(13.20)

(13.21)

If we look at Equation 13.18 as being the inverse Fourier transform of Equation 13.21 and sample a(t) at t=k, we have

(13.22)

(13.23)

but this integral is the form of an inverse discrete-time Fourier transform (DTFT) which means

(13.24)

If the integer translates of φ(t) are orthogonal, a(k)=δ(k) and we have our result

(13.25)

If the scaling function is not normalized

(13.26)

which is similar to Parseval's theorem relating the energy in the frequency domain to the energy in the time domain.

Proof 6 Equation Equation 6.20 states a very interesting property of the frequency response of an FIR filter with the scaling coefficients as filter coefficients. This result can be derived in the frequency or time domain. We will show the frequency domain argument. The scaling equation Equation 13.1 becomes Equation 6.51 in the frequency domain. Taking the squared magnitude of both sides of a scaled version of

(13.27)

gives

(13.28)

Add kπ to ω and sum over k to give for the left side of Equation 13.28

(13.29)

which is unity from Equation 6.57. Summing the right side of Equation 13.28 gives

(13.30)

Break this sum into a sum of the even and odd indexed terms.

(13.31)

(13.32)

which after using Equation 13.29 gives

(13.33)

which gives Equation 6.20. This requires both the scaling and orthogonal relations but no specific normalization of φ(t). If viewed as an FIR filter, h(n) is called a quadrature mirror filter (QMF) because of the symmetry of its frequency response about π.

Proof 10 The multiresolution assumptions in ??? require the scaling function and wavelet satisfy Equation 6.1 and Equation 3.24

(13.34)

and orthonormality requires

(13.35)

and

(13.36)

for all k∈Z. Substituting Equation 13.34 into Equation 13.36 gives

(13.37)

Rearranging and making a change of variables gives

(13.38)

Using Equation 13.35 gives

(13.39)

for all k∈Z. Summing over ℓ gives

(13.40)

Separating Equation 13.40 into even and odd indices gives

(13.41)

which must be true for all integer k. Defining h_e(n)=h(2n), h_o(n)=h(2n+1) and 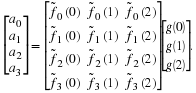for any sequence g, this becomes

(13.42)

From the orthonormality of the translates of φ and ψ one can similarly obtain the following:

(13.43)

(13.44)

This can be compactly represented as

(13.45)

Assuming the sequences are finite length Equation 13.45 can be used to show that

where δ_k(n)=δ(n–k). Indeed, taking the Z-transform of