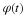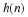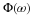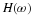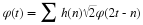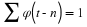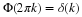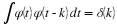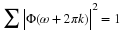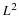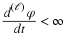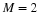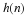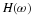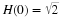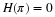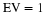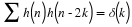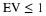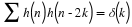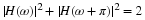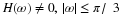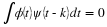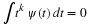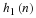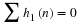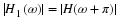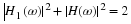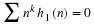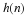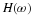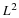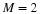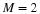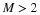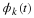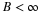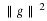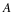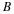In this appendix we develop most of the results on scaling functions, wavelets and scaling and wavelet coefficients presented in Section 6.8 and elsewhere. For convenience, we repeat Equation 6.1, Equation 6.10, Equation 6.13, and Equation 6.15 here

(14.1)

(14.2)

(14.3)

If normalized

(14.4)

The results in this appendix refer to equations in the text written in bold face fonts.

Equation Equation 6.45 is the normalization of Equation 6.15 and part of the orthonormal conditions required by Equation 14.3 for k=0 and E=1.

Equation Equation 6.53 If the φ(x–k) are orthogonal, Equation 14.3 states

(14.5)

Summing both sides over m gives

(14.6)

which after reordering is

(14.7)

Using Equation 6.50, Equation 14.21, and Equation 14.24 gives

(14.8)

but 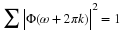from Equation 14.19, therefore

(14.9)

If the scaling function is not normalized to unity, one can show the more general result of Equation 6.53. This is done by noting that a more general form of Equation 6.50 is

(14.10)

if one does not normalize A₀=1 in Equation 14.20 through Equation 14.24.

Equation Equation 6.53 follows from summing Equation 14.3 over m as

(14.11)

which after reordering gives

(14.12)

and using Equation 14.10 gives Equation 6.53.

Equation Equation 6.46 is derived by applying the basic recursion equation to its own right hand side to give

(14.13)

which, with a change of variables of ℓ=2n+k and reordering of operation, becomes

(14.14)

Applying this j times gives the result in Equation 6.46. A similar result can be derived for the wavelet.

Equation Equation 6.48 is derived by defining the sum

(14.15)

and using the basic recursive equation Equation 14.1 to give

(14.16)

Interchanging the order of summation gives

(14.17)

but the summation over ℓ is independent of an integer shift so that using Equation 14.2 and Equation 14.15 gives

(14.18)

This is the linear difference equation

(14.19)

which has as a solution the geometric sequence

(14.20)

If the limit exists, equation Equation 14.15 divided by 2^J is the Riemann sum whose limit is the definition of the Riemann integral of φ(x)

(14.21)

It is stated in Equation 6.57 and shown in Equation 14.6 that if φ(x) is normalized, then A₀=1 and Equation 14.20 becomes

which gives Equation 6.48.

Equation Equation 14.21 shows another remarkable property of φ(x) in that the bracketed term is exactly equal to the integral, independent of J. No limit need be taken!

Equation Equation 6.49 is the “partitioning of unity" by φ(x). It follows from Equation 6.48 by setting J=0.

Equation Equation 6.50 is generalization of Equation 6.49 by noting that the sum in Equation 6.48 is independent of a shift of the form

(14.23)

for any integers M≥J and L. In the limit as M→∞, 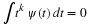can be made arbitrarily close to any x, therefore, if φ(x) is continuous,

(14.24)

This gives Equation 6.50 and becomes Equation 6.49 for J=0. Equation Equation 6.50 is called a “partitioning of unity" for obvious reasons.

The first four relationships for the scaling function hold in a generalized form for the more general defining equation Equation 8.4. Only Equation 6.48 is different. It becomes

(14.25)

for M an integer. It may be possible to show that certain rational M are allowed.

Equations Equation 6.51, Equation 6.72, and Equation 6.52 are the recursive relationship for the Fourier transform of the scaling function and are obtained by simply taking the transform Equation 6.2 of both sides of Equation 14.1 giving

(14.26)

which after the change of variables y=2t–n becomes

(14.27)

and using Equation 6.3 gives

(14.28)

which is Equation 6.51 and Equation 6.72. Applying this recursively gives the infinite product Equation 6.52 which holds for any normalization.

Equation Equation 6.57 states that the sum of the squares of samples of the Fourier transform of the scaling function is one if the samples are uniform every 2π. An alternative derivation to that in Appendix A is shown here by taking the definition of the Fourier transform of φ(x), sampling it every 2πk points and multiplying it times its complex conjugate.

(14.29)

Summing over k gives

(14.30)

(14.31)

(14.32)

but

(14.33)

therefore

(14.34)

which becomes

(14.35)

Because of the orthogonality of integer translates of φ(x), this is not a function of ω but is 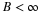which, if normalized, is unity as stated in Equation 6.57. This is the frequency domain equivalent of Equation 6.13.

Equations Equation 6.58 and Equation 6.59 show how the scaling function determines the equation coefficients. This is derived by multiplying both sides of Equation 14.1 by φ(2x–m) and integrating to give

(14.36)

(14.37)

Using the orthogonality condition Equation 14.3 gives

(14.38)

which gives Equation 6.58. A similar argument gives Equation 6.59.