TEASER - 19
SERVING FIRST
Andy (A) and Sandy (S) are facing each other in a tennis match where Andy (A) is serving first in first set;
i What will be the score if Andy retains his service and breaks 1st service of Sandy (S) in the 1st set ?
ii What will be the score if Sandy retains his service and breaks 1st service of Andy in the 1st set ?


THE EXPLANATION:
Andy (A) is serving first in 1st set.
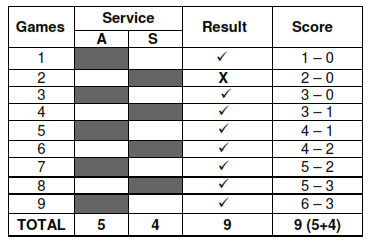
(a) Andy (A) retains his service ( ) and breaks (X) the 1st service of Sandy (S) and wins first set,
Table - a
(b) Sandy (S) retains his service ( ) and breaks (X) the 1st service of Andy (A) and wins first set,
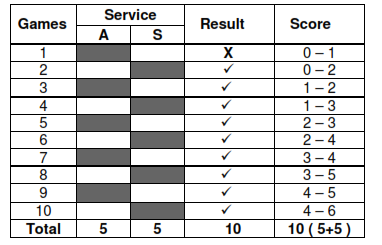
When A breaks 1st service of S (Table - a), the maximum gap created between A and S is of the order of 3 games where as when S breaks 1st service of A (Table-b) the maximum gap is of the order 2 games only. Here A and S do exactly same thing but A achieves a gap of 3 games to 2 of S without doing any thing extra.
It can have a psychological impact on the performance of S. When A breaks 1st service of S, he wins set at 6 - 3 and plays a total of 9 games (Table-a) where as when S breaks 1st service of A, he wins set at 4 - 6 and plays a total of 10 games, one game more than A (Table-b). By breaking only once in the whole set A gets away by playing only 9 games (serves five time to four of S), where as for exactly same number of break S is required to play 10 games for none of his fault, why this discrimination ?
(c) Now, what happens if score line is:

Table - c
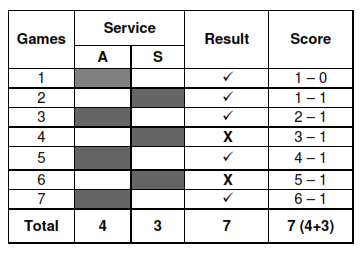
Table – d

The total number of games played (in both cases) (Table - a & b) are seven (1 to 7) with 4 odd numbers (1st, 3rd & 5th) and 3 even numbers (2nd, 4th & 6th). By virtue of serving first, A shall get an opportunity to serve odd numbers (4 times) and S shall have opportunity to serve even numbers. So A gets 4 serves and S gets 3 serves. Therefore, for same score line (6 - 1) A is required to break serve of S only two times (Table-c) where as S toils to break A three times (Table-d).
Why this inequality ?
In all above cases, it is very obvious that A is enjoying a certain amount of advantage over S only because he is serving first. In today’s hyper sports and intense competitive era even a hair line gap advantage may have impact on the final result, especially if winner and loser are of same caliber.
What is the solution: Equality ?:
Each player must be given equal number of services in each set and in each match, so that equal opportunity level is achieved.
Each set / match can be played in two stages.
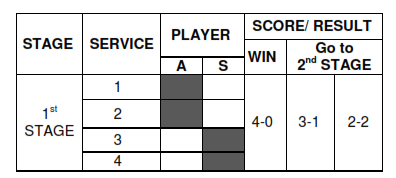
• 1st stage to be of 4 serves in total (2 each continuously).
Whosoever win maximum points with a gap of 4 wins the set else set goes to 2nd stage.
• 2nd stage would consist of maximum of six Steps (S-1 to S-6). Each player will be given one service alternatively at each step. One who wins maximum points with a difference of four (4) at any step wins the set.
• In case of a tie at the end of 6th step, either the set is terminated, irrespective of points difference and points in each set are added at the end of match and winner is decided on the basis of maximum points won cumulatively in a match.
• Alternatively set can continue till a difference of 4 points is achieved. Set itself can be converted into a match beyond a certain point.
1) 1st STAGE: Total: 4 services (2 each with no gap).
2) 2nd STAGE: 2nd stage consists of maximum 12 services

In each set there will be seven (7) opportunity (one in 1st stage & six in 2nd stage) to win the set early. If each set ends in 1st stage itself, match will be over very quickly. It would indicate that the looser is not of equal caliber and match deserves to end fast.
Alternatively, games or points won in each set can be added together at the end of match and who so ever wins maximum points, in whole match (cumulative) with a difference of 4 shall win the match.
********