TEASER - 20
CURSE OF CURVE
Consider there are two humanoid robots K1 and K2. Both have exactly identical capabilities, both run at same speed from start to finish. Now both are competing with each other for 800 m race (cycle) together (pack running) in an indoor stadium with circular / oval track. Who will win?


THE EXPLANATION:
Game at micro-second scale:
In modern day sporting events, the electronic gadgets, like 3rd umpire in cricket or stretched photographs in sprinting are used extensively in order to extract the hair line gap to decide who is in or who is out. This micro-second precision level is rigorously applied in all games and even one hundredth (1/100) of a second or one tenth of an inch is not spared in separating winner from looser.

CLOSE FINISH: REQUIRE MACHINE SCRUTINY
But what is startling is that same precision of microscopic level analysis is seldom applied to the game in entirety to see whether factors other than individual efforts are influencing the results.
There are many events where extraneous factors other than individual effort appear to be influencing the result. One such area is track & field event where tracks are designed in such a way that each lane is different from other and each track is curved at every turn. Although variation in lane qualities may appear miniscule at human scale but can get magnified many time at sub-second (microscopic) scale.
The lanes in 100 m sprint events are all straight and parallel hence are exactly identical, however, in 400 m oval (circular) track, the conditions are not exactly same for all lanes.

FULL CIRCULAR AND SEMI-CIRCULAR TRACKS
The total length of an individual lane (circumference) in case of round track (an extreme case) can be shown as follows:

Or in case of an oval track (semi circular track) the formula for total track length would be as follows;

Now, take for example lane one (L-1) and lane two (L-2) are having radius R1 & R2 of 50 feet & 54 feet respectively, (assuming a minimum lane width of 5 feet) the length of individual lanes would be as follows, (Z being constant for both lane):


Therefore Lane-2 is dissimilar to Lane-1 (1: 0.86) in terms of total distance (end to end). In case of 400 m or longer race, any discrepancy due to this would get multiplied.
The degree of curvature or circularity for each lane can be determined by the ratio between total length of lane (circumference) and total length of maximum number of straight dashes one can make within the limits of an individual lane.

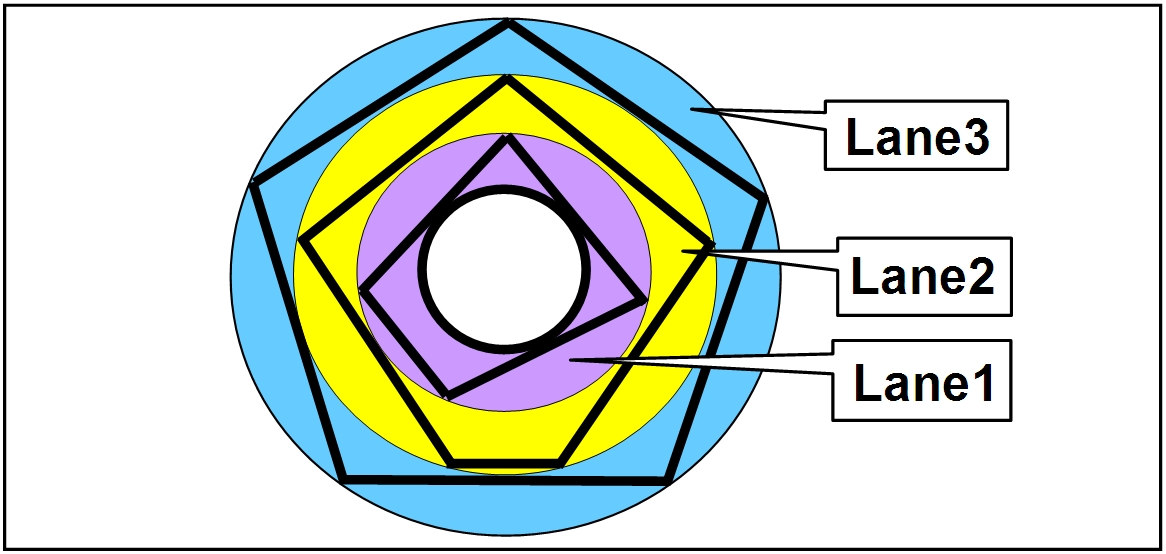
THE OUTER-MOST CIRCULAR TRACK HAS THE LONGEST STRAIGHT DASHES
Lane-3 has 5 straight dashes (SD) of equal length (5SD)
Lane-2 has 4 straight dash of equal length and one is 1/3 (4SD+1/3SD).
Lane-1 has 3 straight dashes of equal length and one is ½ (3SD+1/2SD).
There are three areas of concern in case of oval / circular tracks;
1. The lanes are not 100% equal in terms of total lengths.
2. The lanes are not 100% equal in terms of curvature.
3. The ratio between curvature and straight portions of track are not 100% equal between the lanes.
If two lanes are equal in terms of all characteristics, the ratio should be always 1:1 (100%) between lanes as happens in case of 100 m sprint event. Therefore anything less or more than 100% would mean un-equality among lanes, which when subjected to microscopic level would magnify many times.
Who would win K1 or K2
The races are generally run in packs or individually along single lane. Pack or bunch running involves body touching and constant
fight for inner circle where as independent running does not involve body touching.

PACK RUNNING AND SINGLE LANE RUNNING
In case of pack or bunch running, as long both, K1 and K2 run on straight portion of the track, they will be running side-by-side without body touching, however the moment they enter into curved portion, the one on inside track (say K2), being nearer would occupy the inner circle and would forge ahead of K1 simply because inner side of the curve has less distance. K1, being towards outside, would immediately fall back, as he has to cover longer distance and would remain behind, thereafter till end and finish second. Therefore only one (K1) would win the race.

RUNNING AROUND BENT PART OF A TRACK
On the other hand, independent running, although does not involve body touching and fight for inner circle, one has to tackle the curvature of the track to maintain the speed and body tilt.
The impact on races: the impact of circular track on results can be summarized as follows:
(i) Body Tilt Effect:
The inner most lane has maximum curvature and outer most the least. To overcome lane curvature athletes tilt their body inside proportionate to their speed and curvature so as to avoid falling out of lane due to centrifugal force. Since curvature is variable for each lane the body tilt varies from lane to lane, maximum in inside lane and vice versa. The variable tilting affects the speed and momentum and ultimately the result.

BODY TILTING WHILE NEGOTIATING A BEND
(ii) Cumulative Effect:
The tracks are generally laid in an oval shape where the ratio of straight portion to curved portion of track varies from stadium to stadium. The speed is maximum in straight portion and minimum in curved portion. In case of small indoor stadium, if one is allotted inner lane, he may have to pass through curved portion more frequently than the one allotted outer most lane.
Any amount of variations among lanes, however negligible it may be, can turn into a ‘snow ball’ on a cumulative basis, especially in events where participants are required to run multiple times through same lane.
(iii)Scale Effect:
The impact of curvature may appear miniscule at human scale but can get magnified many times at micro-second level. The impact can be seen more easily in the events such as motorcycle / formula car race where participants need to maintain high speed over a long and tortuous track.

BODY TILT AT BENDS INCREASES WHEN HIGH SPEED IS MAINTAINED
It is evident wide from above that the participants are not provided equal running conditions at same standard of precision as their results are subjected to. Athletes have every right to demand identical conditions on a microscopic scale.
The glaring examples:
The result of 400 m hurdle in 1984 Los Angeles Olympics for bronze medal was subjected to a very high degree of magnification and nothing was spared in denying PT Usha of India a bronze. It was amazing that she was made to loose by one hundredth of a second (1/100 second).
She literally lost by a whisker. The scale of stretching of time and space was amazing and unbelievable. The time difference is so small (1/100 second) that it still amazes even today and creates doubt whether it was her deficiency or track design deficiency that cost her bronze. There can be no doubt that the result would have been definitely different (plus or minus) if she had been allotted another lane than she was running in.

SPRINT QUEEN P.T. USHA OF INDIA
Similarly, Milkha Singh of India, was denied bronze medal in 400 m race in 1960 Rome Olympics by a wafer thin margin of 1/10 seconds, although he had broken the Olympic records.

FLYING SIKH MILKHA SINGH OF INDIA
There may be hundreds of such close cases where doubts would always remain in the minds whether failure was due to extraneous causes. These cases should be put to modern tests involving computer software analysis to see if results were influenced by factors other than individual efforts, such as lane variation, especially over long races.
What is the solution:
1. The dissimilarity among the lanes in a circular track is very obvious, in terms of variable curvature, variable total distance and variable straight to curved ratio.
2. The first and foremost requirement is to thoroughly analyse the existing track & field design at microscopic level with respect to its effect on the outcome of results so as to eliminate any doubt in the minds of participants, especially those who loose by whiskers.
3. In order to achieve identical lane properties, track designs as indicated below can be tried:
a. ASHTAMIUM (8): 8 Shaped Track Design.
• In an ancient Hindu Sanskrit language eight (8) is referred to as Ashtami, hence name Ashtamium.
• Each individual lane is curved at two ends and the product of sum total impact of degree of curvature, elevation, undulation or any other element is always constant for each lane.
• Each lane is of same length of 200 m.
• The lanes do not cross on same level but cross one over the other like an over bridge so as to avoid clashing of athletes.
• The races are always run in 200 m or in multiple of 200 m.
• There is no need to run in packs as several tracks can be accommodated in a single stadium.
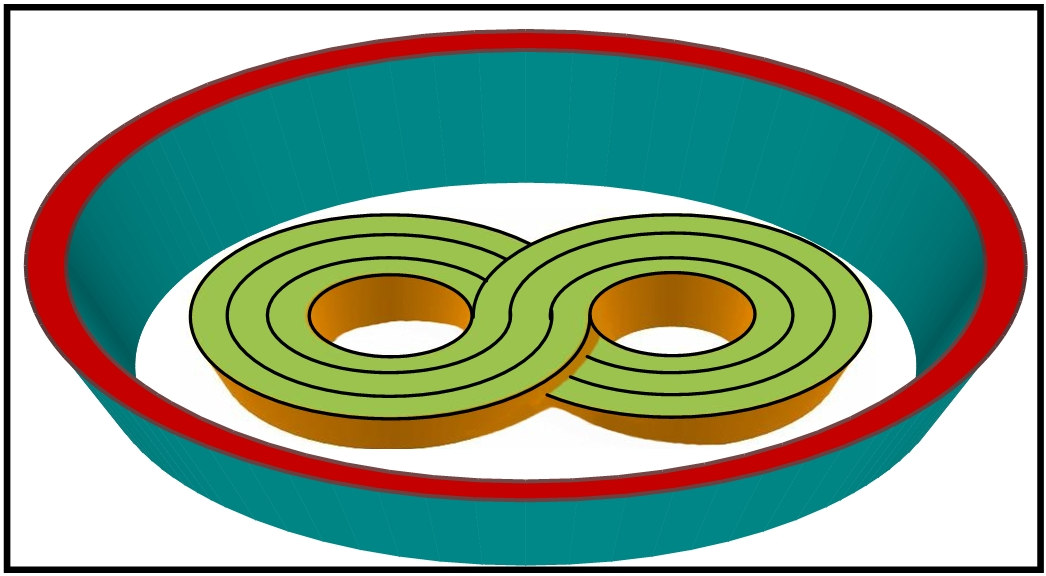
ASHTAMIUM: NEW TRACK DESIGN
b. SWIMMING POOL TYPE RACE TRACK
Another variation could be similar to that of ‘swimming pool type’ where all tracks are parallel and straight. Each individual runs in his own track to and fro (by touching the end of each lane).
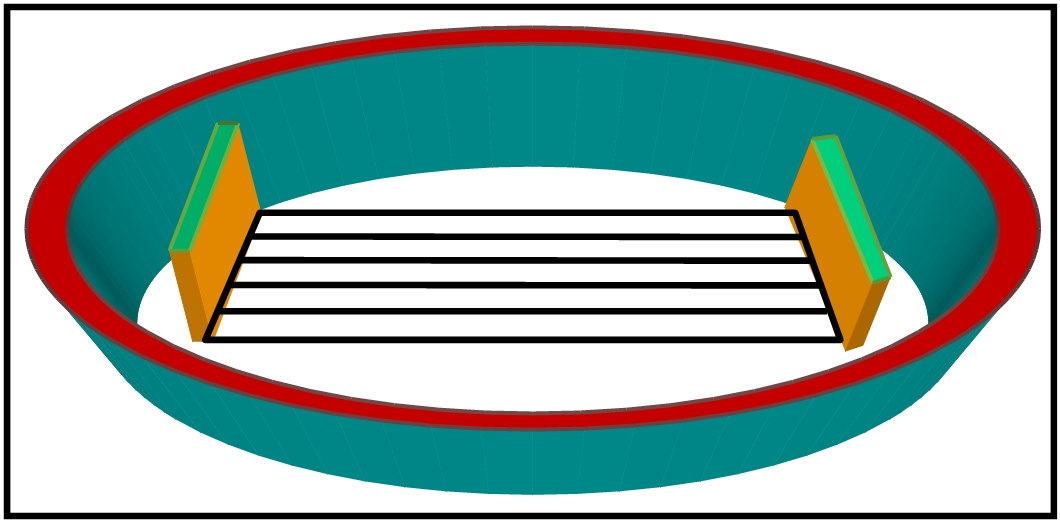
SWIMMING POOL TYPE TRACK DESIGN TRACKS ARE ALL STARIGHT AND PARALLEL
*******





















