Using the given information, we note that the initial velocity and position are zero, and the final position is 1.50 m. The final velocity can be found
using the equation:
2
2
(3.93)
vy = v 0 y − 2 g( y − y 0).
Substituting known values into the equation, we get
2
(3.94)
vy = 02 − 2(9.80 m/s2)( − 1.50 m − 0 m) = 29.4 m2 /s2

CHAPTER 3 | TWO-DIMENSIONAL KINEMATICS 113
yielding
v
(3.95)
y = −5.42 m/s.
We know that the square root of 29.4 has two roots: 5.42 and -5.42. We choose the negative root because we know that the velocity is directed
downwards, and we have defined the positive direction to be upwards. There is no initial horizontal velocity relative to the plane and no horizontal
acceleration, and so the motion is straight down relative to the plane.
Solution for (b)
Because the initial vertical velocity is zero relative to the ground and vertical motion is independent of horizontal motion, the final vertical velocity
for the coin relative to the ground is vy = − 5.42 m/s , the same as found in part (a). In contrast to part (a), there now is a horizontal
component of the velocity. However, since there is no horizontal acceleration, the initial and final horizontal velocities are the same and
vx = 260 m/s . The x- and y-components of velocity can be combined to find the magnitude of the final velocity:
(3.96)
v = v 2
2
x + vy .
Thus,
(3.97)
v = (260 m/s)2 + ( − 5.42 m/s)2
yielding
v
(3.98)
= 260.06 m/s.
The direction is given by:
(3.99)
θ = tan−1( vy / vx) = tan−1( − 5.42 / 260)
so that
(3.100)
θ = tan−1( − 0.0208) = −1.19º.
Discussion
In part (a), the final velocity relative to the plane is the same as it would be if the coin were dropped from rest on the Earth and fell 1.50 m. This
result fits our experience; objects in a plane fall the same way when the plane is flying horizontally as when it is at rest on the ground. This result
is also true in moving cars. In part (b), an observer on the ground sees a much different motion for the coin. The plane is moving so fast
horizontally to begin with that its final velocity is barely greater than the initial velocity. Once again, we see that in two dimensions, vectors do not
add like ordinary numbers—the final velocity v in part (b) is not (260 – 5.42) m/s ; rather, it is 260.06 m/s . The velocity’s magnitude had to be
calculated to five digits to see any difference from that of the airplane. The motions as seen by different observers (one in the plane and one on
the ground) in this example are analogous to those discussed for the binoculars dropped from the mast of a moving ship, except that the velocity
of the plane is much larger, so that the two observers see very different paths. (See Figure 3.50.) In addition, both observers see the coin fall
1.50 m vertically, but the one on the ground also sees it move forward 144 m (this calculation is left for the reader). Thus, one observer sees a
vertical path, the other a nearly horizontal path.
Making Connections: Relativity and Einstein
Because Einstein was able to clearly define how measurements are made (some involve light) and because the speed of light is the same
for all observers, the outcomes are spectacularly unexpected. Time varies with observer, energy is stored as increased mass, and more
surprises await.
PhET Explorations: Motion in 2D
Try the new "Ladybug Motion 2D" simulation for the latest updated version. Learn about position, velocity, and acceleration vectors. Move the
ball with the mouse or let the simulation move the ball in four types of motion (2 types of linear, simple harmonic, circle).
Figure 3.51 Motion in 2D (http://cnx.org/content/m42045/1.7/motion-2d_en.jar)
Glossary
air resistance: a frictional force that slows the motion of objects as they travel through the air; when solving basic physics problems, air resistance
is assumed to be zero
analytical method: the method of determining the magnitude and direction of a resultant vector using the Pythagorean theorem and trigonometric
identities
114 CHAPTER 3 | TWO-DIMENSIONAL KINEMATICS
classical relativity: the study of relative velocities in situations where speeds are less than about 1% of the speed of light—that is, less than 3000
km/s
commutative: refers to the interchangeability of order in a function; vector addition is commutative because the order in which vectors are added
together does not affect the final sum
component (of a 2-d vector): a piece of a vector that points in either the vertical or the horizontal direction; every 2-d vector can be expressed as
a sum of two vertical and horizontal vector components
direction (of a vector): the orientation of a vector in space
head (of a vector): the end point of a vector; the location of the tip of the vector’s arrowhead; also referred to as the “tip”
head-to-tail method: a method of adding vectors in which the tail of each vector is placed at the head of the previous vector
kinematics: the study of motion without regard to mass or force
magnitude (of a vector): the length or size of a vector; magnitude is a scalar quantity
motion: displacement of an object as a function of time
projectile motion: the motion of an object that is subject only to the acceleration of gravity
projectile: an object that travels through the air and experiences only acceleration due to gravity
range: the maximum horizontal distance that a projectile travels
relative velocity: the velocity of an object as observed from a particular reference frame
relativity: the study of how different observers moving relative to each other measure the same phenomenon
resultant vector: the vector sum of two or more vectors
resultant: the sum of two or more vectors
scalar: a quantity with magnitude but no direction
tail: the start point of a vector; opposite to the head or tip of the arrow
trajectory: the path of a projectile through the air
vector addition: the rules that apply to adding vectors together
vector: a quantity that has both magnitude and direction; an arrow used to represent quantities with both magnitude and direction
velocity: speed in a given direction
Section Summary
3.1 Kinematics in Two Dimensions: An Introduction
• The shortest path between any two points is a straight line. In two dimensions, this path can be represented by a vector with horizontal and
vertical components.
• The horizontal and vertical components of a vector are independent of one another. Motion in the horizontal direction does not affect motion in
the vertical direction, and vice versa.
3.2 Vector Addition and Subtraction: Graphical Methods
• The graphical method of adding vectors A and B involves drawing vectors on a graph and adding them using the head-to-tail method. The
resultant vector R is defined such that A + B = R . The magnitude and direction of R are then determined with a ruler and protractor,
respectively.
• The graphical method of subtracting vector B from A involves adding the opposite of vector B , which is defined as −B . In this case,
A – B = A + (–B) = R . Then, the head-to-tail method of addition is followed in the usual way to obtain the resultant vector R .
• Addition of vectors is commutative such that A + B = B + A .
• The head-to-tail method of adding vectors involves drawing the first vector on a graph and then placing the tail of each subsequent vector at
the head of the previous vector. The resultant vector is then drawn from the tail of the first vector to the head of the final vector.
• If a vector A is multiplied by a scalar quantity c , the magnitude of the product is given by cA . If c is positive, the direction of the product
points in the same direction as A ; if c is negative, the direction of the product points in the opposite direction as A .
3.3 Vector Addition and Subtraction: Analytical Methods
• The analytical method of vector addition and subtraction involves using the Pythagorean theorem and trigonometric identities to determine the
magnitude and direction of a resultant vector.
• The steps to add vectors A and B using the analytical method are as follows:
Step 1: Determine the coordinate system for the vectors. Then, determine the horizontal and vertical components of each vector using the
equations
CHAPTER 3 | TWO-DIMENSIONAL KINEMATICS 115
Ax = A cos θ
Bx = B cos θ
and
Ay = A sin θ
By = B sin θ.
Step 2: Add the horizontal and vertical components of each vector to determine the components Rx and Ry of the resultant vector, R :
Rx = Ax + Bx
and
Ry = Ay + By.
Step 3: Use the Pythagorean theorem to determine the magnitude, R , of the resultant vector R :
R = R 2
2
x + Ry.
Step 4: Use a trigonometric identity to determine the direction, θ , of R :
θ = tan−1( Ry / Rx).
3.4 Projectile Motion
• Projectile motion is the motion of an object through the air that is subject only to the acceleration of gravity.
• To solve projectile motion problems, perform the following steps:
1. Determine a coordinate system. Then, resolve the position and/or velocity of the object in the horizontal and vertical components. The
components of position s are given by the quantities x and y , and the components of the velocity v are given by vx = v cos θ and vy = v sin θ , where v is the magnitude of the velocity and θ is its direction.
2. Analyze the motion of the projectile in the horizontal direction using the following equations:
Horizontal motion( ax = 0)
x = x 0 + vxt
vx = v 0 x = vx = velocity is a constant.
3. Analyze the motion of the projectile in the vertical direction using the following equations:
Vertical motion(Assuming positive direction is up; ay = − g = −9.80 m/s2)
y = y 0 + 12( v 0 y + vy) t
vy = v 0 y − gt
y = y 0 + v 0 yt − 12 gt 2
v 2
2
y = v 0 y − 2 g( y − y 0).
4. Recombine the horizontal and vertical components of location and/or velocity using the following equations:
s = x 2 + y 2
θ = tan−1( y / x)
v = v 2
2
x + vy
θ v = tan−1( vy / vx).
• The maximum height h of a projectile launched with initial vertical velocity v 0 y is given by
v 2
h = 0 y
2 g .
• The maximum horizontal distance traveled by a projectile is called the range. The range R of a projectile on level ground launched at an angle
θ 0 above the horizontal with initial speed v 0 is given by
v 2
R = 0 sin 2 θ 0
g
.
3.5 Addition of Velocities
• Velocities in two dimensions are added using the same analytical vector techniques, which are rewritten as
vx = v cos θ
vy = v sin θ
v = v 2
2
x + vy
116 CHAPTER 3 | TWO-DIMENSIONAL KINEMATICS
θ = tan−1( vy / vx).
• Relative velocity is the velocity of an object as observed from a particular reference frame, and it varies dramatically with reference frame.
• Relativity is the study of how different observers measure the same phenomenon, particularly when the observers move relative to one
another. Classical relativity is limited to situations where speed is less than about 1% of the speed of light (3000 km/s).
Conceptual Questions
3.2 Vector Addition and Subtraction: Graphical Methods
1. Which of the following is a vector: a person’s height, the altitude on Mt. Everest, the age of the Earth, the boiling point of water, the cost of this
book, the Earth’s population, the acceleration of gravity?
2. Give a specific example of a vector, stating its magnitude, units, and direction.
3. What do vectors and scalars have in common? How do they differ?
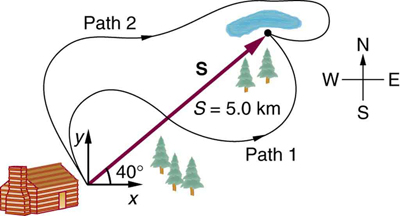
4. Two campers in a national park hike from their cabin to the same spot on a lake, each taking a different path, as illustrated below. The total
distance traveled along Path 1 is 7.5 km, and that along Path 2 is 8.2 km. What is the final displacement of each camper?
Figure 3.52
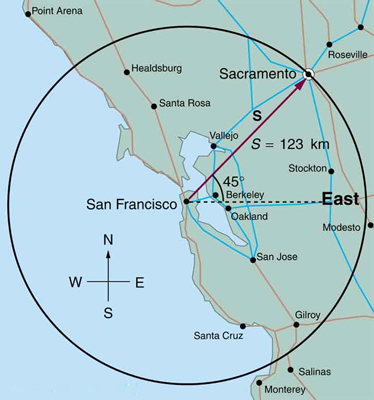
5. If an airplane pilot is told to fly 123 km in a straight line to get from San Francisco to Sacramento, explain why he could end up anywhere on the
circle shown in Figure 3.53. What other information would he need to get to Sacramento?
Figure 3.53
6. Suppose you take two steps A and B (that is, two nonzero displacements). Under what circumstances can you end up at your starting point?
More generally, under what circumstances can two nonzero vectors add to give zero? Is the maximum distance you can end up from the starting
point A + B the sum of the lengths of the two steps?
7. Explain why it is not possible to add a scalar to a vector.
8. If you take two steps of different sizes, can you end up at your starting point? More generally, can two vectors with different magnitudes ever add to
zero? Can three or more?
3.3 Vector Addition and Subtraction: Analytical Methods
9. Suppose you add two vectors A and B . What relative direction between them produces the resultant with the greatest magnitude? What is the
maximum magnitude? What relative direction between them produces the resultant with the smallest magnitude? What is the minimum magnitude?
10. Give an example of a nonzero vector that has a component of zero.
11. Explain why a vector cannot have a component greater than its own magnitude.
CHAPTER 3 | TWO-DIMENSIONAL KINEMATICS 117
12. If the vectors A and B are perpendicular, what is the component of A along the direction of B ? What is the component of B along the
direction of A ?
3.4 Projectile Motion
13. Answer the following questions for projectile motion on level ground assuming negligible air resistance (the initial angle being neither 0º nor 90º
): (a) Is the velocity ever zero? (b) When is the velocity a minimum? A maximum? (c) Can the velocity ever be the same as the initial velocity at a time
other than at t = 0 ? (d) Can the speed ever be the same as the initial speed at a time other than at t = 0 ?
14. Answer the following questions for projectile motion on level ground assuming negligible air resistance (the initial angle being neither 0º nor 90º
): (a) Is the acceleration ever zero? (b) Is the acceleration ever in the same direction as a component of velocity? (c) Is the acceleration ever opposite
in direction to a component of velocity?
15. For a fixed initial speed, the range of a projectile is determined by the angle at which it is fired. For all but the maximum, there are two angles that
give the same range. Considering factors that might affect the ability of an archer to hit a target, such as wind, explain why the smaller angle (closer
to the horizontal) is preferable. When would it be necessary for the archer to use the larger angle? Why does the punter in a football game use the
higher trajectory?
16. During a lecture demonstration, a professor places two coins on the edge of a table. She then flicks one of the coins horizontally off the table,
simultaneously nudging the other over the edge. Describe the subsequent motion of the two coins, in particular discussing whether they hit the floor
at the same time.
3.5 Addition of Velocities
17. What frame or frames of reference do you instinctively use when driving a car? When flying in a commercial jet airplane?
18. A basketball player dribbling down the court usually keeps his eyes fixed on the players around him. He is moving fast. Why doesn’t he need to
keep his eyes on the ball?
19. If someone is riding in the back of a pickup truck and throws a softball straight backward, is it possible for the ball to fall straight down as viewed
by a person standing at the side of the road? Under what condition would this occur? How would the motion of the ball appear to the person who
threw it?
20. The hat of a jogger running at constant velocity falls off the back of his head. Draw a sketch showing the path of the hat in the jogger’s frame of
reference. Draw its path as viewed by a stationary observer.
21. A clod of dirt falls from the bed of a moving truck. It strikes the ground directly below the end of the truck. What is the direction of its velocity
relative to the truck just before it hits? Is this the same as the direction of its velocity relative to ground just before it hits? Explain your answers.

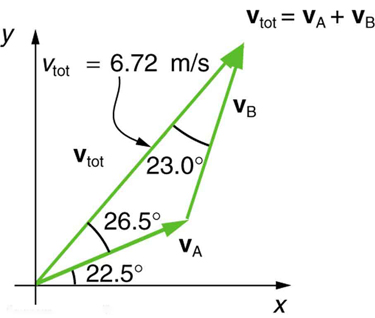
118 CHAPTER 3 | TWO-DIMENSIONAL KINEMATICS
Problems & Exercises
3.2 Vector Addition and Subtraction: Graphical Methods
Use graphical methods to solve these problems. You may assume
data taken from graphs is accurate to three digits.
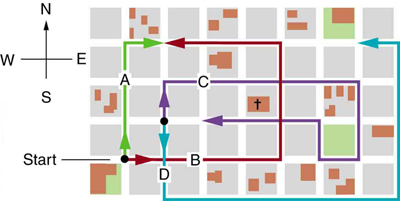
1. Find the following for path A in Figure 3.54: (a) the total distance
traveled, and (b) the magnitude and direction of the displacement from
start to finish.
Figure 3.56
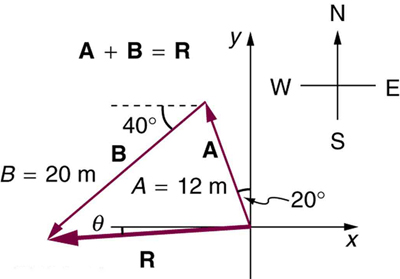
6. Repeat the problem above, but reverse the order of the two legs of the
walk; show that you get the same final result. That is, you first walk leg
B , which is 20.0 m in a direction exactly 40º south of west, and then
leg A , which is 12.0 m in a direction exactly 20º west of north. (This
problem shows that A + B = B + A .)
Figure 3.54 The various lines represent paths taken by different people walking in a
7. (a) Repeat the problem two problems prior, but for the second leg you
city. All blocks are 120 m on a side.
walk 20.0 m in a direction 40.0º north of east (which is equivalent to
2. Find the following for path B in Figure 3.54: (a) the total distance
subtracting B from A —that is, to finding R′ = A − B ). (b) Repeat
traveled, and (b) the magnitude and direction of the displacement from
start to finish.
the problem two problems prior, but now you first walk 20.0 m in a
direction 40.0º south of west and then 12.0 m in a direction 20.0º east
3. Find the north and east components of the displacement for the hikers
shown in Figure 3.52.
of south (which is equivalent to subtracting A from B —that is, to
4. Suppose you walk 18.0 m straight west and then 25.0 m straight north.
finding R′′ = B - A = - R′ ). Show that this is the case.
How far are you from your starting point, and what is the compass
8. Show that the order of addition of three vectors does not affect their
direction of a line connecting your starting point to your final position? (If
sum. Show this property by choosing any three vectors A , B , and C , <










