Step 2. Treat the motion as two independent one-dimensional motions, one horizontal and the other vertical. The kinematic equations for horizontal
and vertical motion take the following forms:
(3.33)
Horizontal Motion( ax = 0)
x = x
(3.34)
0 + vxt
v
(3.35)
x = v 0 x = vx = velocity is a constant.
(3.36)
Vertical Motion(assuming positive is up ay = − g = −9.80m/s2)
102 CHAPTER 3 | TWO-DIMENSIONAL KINEMATICS
(3.37)
y = y 0 + 12( v 0 y + vy) t
v
(3.38)
y = v 0 y − gt
(3.39)
y = y 0 + v 0 yt − 12 gt 2
2
2
(3.40)
vy = v 0 y − 2 g( y − y 0).
Step 3. Solve for the unknowns in the two separate motions—one horizontal and one vertical. Note that the only common variable between the
motions is time t . The problem solving procedures here are the same as for one-dimensional kinematics and are illustrated in the solved examples
below.
Step 4. Recombine the two motions to find the total displacement s and velocity v . Because the x - and y -motions are perpendicular, we determine these vectors by using the techniques outlined in the Vector Addition and Subtraction: Analytical Methods and employing A = A 2
2
x + Ay and
θ = tan−1( Ay / Ax) in the following form, where θ is the direction of the displacement s and θv is the direction of the velocity v : Total displacement and velocity
(3.41)
s = x 2 + y 2
(3.42)
θ = tan−1( y / x)
(3.43)
v = v 2
2
x + vy
(3.44)
θv = tan−1( vy / vx).
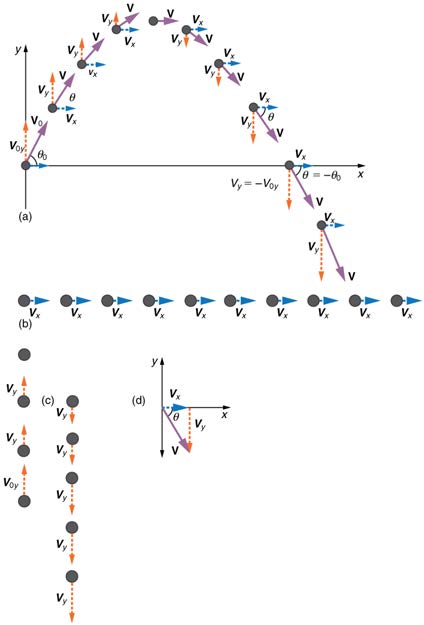
Figure 3.38 (a) We analyze two-dimensional projectile motion by breaking it into two independent one-dimensional motions along the vertical and horizontal axes. (b) The
horizontal motion is simple, because ax = 0 and vx is thus constant. (c) The velocity in the vertical direction begins to decrease as the object rises; at its highest point, the vertical velocity is zero. As the object falls towards the Earth again, the vertical velocity increases again in magnitude but points in the opposite direction to the initial vertical velocity. (d) The x - and y -motions are recombined to give the total velocity at any given point on the trajectory.
Example 3.4 A Fireworks Projectile Explodes High and Away
During a fireworks display, a shell is shot into the air with an initial speed of 70.0 m/s at an angle of 75.0º above the horizontal, as illustrated in
Figure 3.39. The fuse is timed to ignite the shell just as it reaches its highest point above the ground. (a) Calculate the height at which the shell
explodes. (b) How much time passed between the launch of the shell and the explosion? (c) What is the horizontal displacement of the shell
when it explodes?
Strategy
CHAPTER 3 | TWO-DIMENSIONAL KINEMATICS 103
Because air resistance is negligible for the unexploded shell, the analysis method outlined above can be used. The motion can be broken into
horizontal and vertical motions in which ax = 0 and ay = – g . We can then define x 0 and y 0 to be zero and solve for the desired
quantities.
Solution for (a)
By “height” we mean the altitude or vertical position y above the starting point. The highest point in any trajectory, called the apex, is reached
when vy = 0 . Since we know the initial and final velocities as well as the initial position, we use the following equation to find y :
2
2
(3.45)
vy = v 0 y − 2 g( y − y 0).
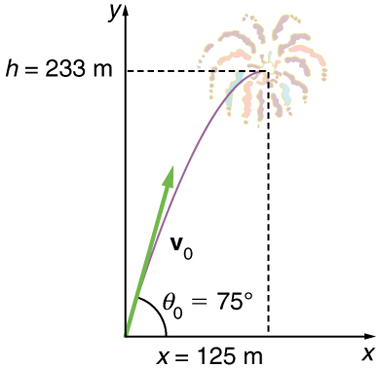
Figure 3.39 The trajectory of a fireworks shell. The fuse is set to explode the shell at the highest point in its trajectory, which is found to be at a height of 233 m and 125 m away horizontally.
Because y 0 and vy are both zero, the equation simplifies to
2
(3.46)
0 = v 0 y − 2 gy.
Solving for y gives
2
(3.47)
v
y = 0 y
2 g .
Now we must find v 0 y , the component of the initial velocity in the y-direction. It is given by v 0 y = v 0 sin θ , where v 0 y is the initial velocity of 70.0 m/s, and θ 0 = 75.0º is the initial angle. Thus,
v
(3.48)
0 y = v 0 sin θ 0 = (70.0 m/s)(sin 75º) = 67.6 m/s.
and y is
(3.49)
y = (67.6 m/s)2 ,
2(9.80 m/s2)
so that
y
(3.50)
= 233m.
Discussion for (a)
Note that because up is positive, the initial velocity is positive, as is the maximum height, but the acceleration due to gravity is negative. Note
also that the maximum height depends only on the vertical component of the initial velocity, so that any projectile with a 67.6 m/s initial vertical
component of velocity will reach a maximum height of 233 m (neglecting air resistance). The numbers in this example are reasonable for large
fireworks displays, the shells of which do reach such heights before exploding. In practice, air resistance is not completely negligible, and so the
initial velocity would have to be somewhat larger than that given to reach the same height.
Solution for (b)
As in many physics problems, there is more than one way to solve for the time to the highest point. In this case, the easiest method is to use
y = y 0 + 12( v 0 y + vy) t . Because y 0 is zero, this equation reduces to simply
(3.51)
y = 12( v 0 y + vy) t.
104 CHAPTER 3 | TWO-DIMENSIONAL KINEMATICS
Note that the final vertical velocity, vy , at the highest point is zero. Thus,
(3.52)
t =
2 y
( v 0y + vy) = 2(233 m)
(67.6 m/s)
= 6.90 s.
Discussion for (b)
This time is also reasonable for large fireworks. When you are able to see the launch of fireworks, you will notice several seconds pass before
the shell explodes. (Another way of finding the time is by using y = y 0 + v 0 yt − 12 gt 2 , and solving the quadratic equation for t .) Solution for (c)
Because air resistance is negligible, ax = 0 and the horizontal velocity is constant, as discussed above. The horizontal displacement is
horizontal velocity multiplied by time as given by x = x 0 + vxt , where x 0 is equal to zero:
x = v
(3.53)
xt,
where vx is the x-component of the velocity, which is given by vx = v 0 cos θ 0 . Now,
v
(3.54)
x = v 0 cos θ 0 = (70.0 m/s)(cos 75.0º) = 18.1 m/s.
The time t for both motions is the same, and so x is
x
(3.55)
= (18.1 m/s)(6.90 s) = 125 m.
Discussion for (c)
The horizontal motion is a constant velocity in the absence of air resistance. The horizontal displacement found here could be useful in keeping
the fireworks fragments from falling on spectators. Once the shell explodes, air resistance has a major effect, and many fragments will land
directly below.
In solving part (a) of the preceding example, the expression we found for y is valid for any projectile motion where air resistance is negligible. Call
the maximum height y = h ; then,
2
(3.56)
v
h = 0 y
2 g .
This equation defines the maximum height of a projectile and depends only on the vertical component of the initial velocity.
Defining a Coordinate System
It is important to set up a coordinate system when analyzing projectile motion. One part of defining the coordinate system is to define an origin
for the x and y positions. Often, it is convenient to choose the initial position of the object as the origin such that x 0 = 0 and y 0 = 0 . It is
also important to define the positive and negative directions in the x and y directions. Typically, we define the positive vertical direction as
upwards, and the positive horizontal direction is usually the direction of the object’s motion. When this is the case, the vertical acceleration, g ,
takes a negative value (since it is directed downwards towards the Earth). However, it is occasionally useful to define the coordinates differently.
For example, if you are analyzing the motion of a ball thrown downwards from the top of a cliff, it may make sense to define the positive direction
downwards since the motion of the ball is solely in the downwards direction. If this is the case, g takes a positive value.
Example 3.5 Calculating Projectile Motion: Hot Rock Projectile
Kilauea in Hawaii is the world’s most continuously active volcano. Very active volcanoes characteristically eject red-hot rocks and lava rather
than smoke and ash. Suppose a large rock is ejected from the volcano with a speed of 25.0 m/s and at an angle 35.0º above the horizontal, as
shown in Figure 3.40. The rock strikes the side of the volcano at an altitude 20.0 m lower than its starting point. (a) Calculate the time it takes the
rock to follow this path. (b) What are the magnitude and direction of the rock’s velocity at impact?
CHAPTER 3 | TWO-DIMENSIONAL KINEMATICS 105
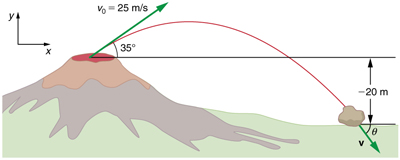
Figure 3.40 The trajectory of a rock ejected from the Kilauea volcano.
Strategy
Again, resolving this two-dimensional motion into two independent one-dimensional motions will allow us to solve for the desired quantities. The
time a projectile is in the air is governed by its vertical motion alone. We will solve for t first. While the rock is rising and falling vertically, the
horizontal motion continues at a constant velocity. This example asks for the final velocity. Thus, the vertical and horizontal results will be
recombined to obtain v and θv at the final time t determined in the first part of the example.
Solution for (a)
While the rock is in the air, it rises and then falls to a final position 20.0 m lower than its starting altitude. We can find the time for this by using
(3.57)
y = y 0 + v 0 yt − 12 gt 2.
If we take the initial position y 0 to be zero, then the final position is y = −20.0 m. Now the initial vertical velocity is the vertical component of
the initial velocity, found from v 0 y = v 0 sin θ 0 = ( 25.0 m/s )( sin 35.0º ) = 14.3 m/s . Substituting known values yields
(3.58)
−20.0 m = (14.3 m/s) t − ⎛⎝4.90 m/s2⎞⎠ t 2.
Rearranging terms gives a quadratic equation in t :
⎛
(3.59)
⎝4.90 m/s2⎞⎠ t 2 − (14.3 m/s) t − (20.0 m) = 0.
This expression is a quadratic equation of the form at 2 + bt + c = 0 , where the constants are a = 4.90 , b = – 14.3 , and c = – 20.0. Its solutions are given by the quadratic formula:
(3.60)
t = − b ± b 2 − 4 ac
2 a
.
This equation yields two solutions: t = 3.96 and t = – 1.03 . (It is left as an exercise for the reader to verify these solutions.) The time is
t = 3.96 s or – 1.03 s . The negative value of time implies an event before the start of motion, and so we discard it. Thus,
t
(3.61)
= 3.96 s.
Discussion for (a)
The time for projectile motion is completely determined by the vertical motion. So any projectile that has an initial vertical velocity of 14.3 m/s and
lands 20.0 m below its starting altitude will spend 3.96 s in the air.
Solution for (b)
From the information now in hand, we can find the final horizontal and vertical velocities vx and vy and combine them to find the total velocity
v and the angle θ 0 it makes with the horizontal. Of course, vx is constant so we can solve for it at any horizontal location. In this case, we
chose the starting point since we know both the initial velocity and initial angle. Therefore:
v
(3.62)
x = v 0 cos θ 0 = (25.0 m/s)(cos 35º) = 20.5 m/s.
The final vertical velocity is given by the following equation:
v
(3.63)
y = v 0 y − gt,
where v 0y was found in part (a) to be 14.3 m/s . Thus,
(3.64)
vy = 14.3 m/s − (9.80 m/s2)(3.96 s)
so that
v
(3.65)
y = −24.5 m/s.
To find the magnitude of the final velocity v we combine its perpendicular components, using the following equation:
106 CHAPTER 3 | TWO-DIMENSIONAL KINEMATICS
(3.66)
v = v 2
2
x + vy = (20.5 m/s)2 + ( − 24.5 m/s)2,
which gives
v
(3.67)
= 31.9 m/s.
The direction θv is found from the equation:
(3.68)
θv = tan−1( vy / vx)
so that
(3.69)
θv = tan−1( − 24.5 / 20.5) = tan−1( − 1.19).
Thus,
θ
(3.70)
v = −50.1 º .
Discussion for (b)
The negative angle means that the velocity is 50.1º below the horizontal. This result is consistent with the fact that the final vertical velocity is
negative and hence downward—as you would expect because the final altitude is 20.0 m lower than the initial altitude. (See Figure 3.40.)
One of the most important things illustrated by projectile motion is that vertical and horizontal motions are independent of each other. Galileo was the
first person to fully comprehend this characteristic. He used it to predict the range of a projectile. On level ground, we define range to be the
horizontal distance R traveled by a projectile. Galileo and many others were interested in the range of projectiles primarily for military
purposes—such as aiming cannons. However, investigating the range of projectiles can shed light on other interesting phenomena, such as the orbits
of satellites around the Earth. Let us consider projectile range further.
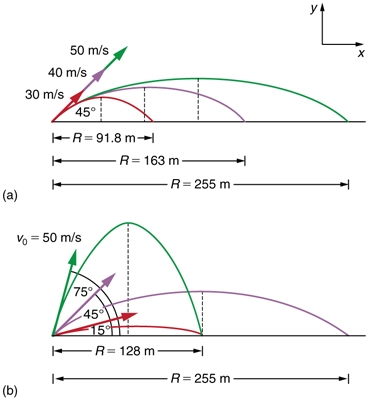
Figure 3.41 Trajectories of projectiles on level ground. (a) The greater the initial speed v 0 , the greater the range for a given initial angle. (b) The effect of initial angle θ 0 on the range of a projectile with a given initial speed. Note that the range is the same for 15º and 75º , although the maximum heights of those paths are different.
How does the initial velocity of a projectile affect its range? Obviously, the greater the initial speed v 0 , the greater the range, as shown in Figure
3.41(a). The initial angle θ 0 also has a dramatic effect on the range, as illustrated in Figure 3.41(b). For a fixed initial speed, such as might be produced by a cannon, the maximum range is obtained with θ 0 = 45º . This is true only for conditions neglecting air resistance. If air resistance is
considered, the maximum angle is approximately 38º . Interestingly, for every initial angle except 45º , there are two angles that give the same
range—the sum of those angles is 90º . The range also depends on the value of the acceleration of gravity g . The lunar astronaut Alan Shepherd
was able to drive a golf ball a great distance on the Moon because gravity is weaker there. The range R of a projectile on level ground for which air
resistance is negligible is given by
2
(3.71)
v
R = 0 sin 2 θ 0
g
,
where v 0 is the initial speed and θ 0 is the initial angle relative to the horizontal. The proof of this equation is left as an end-of-chapter problem
(hints are given), but it does fit the major features of projectile range as described.
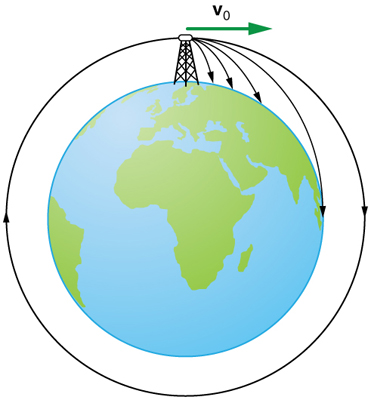

CHAPTER 3 | TWO-DIMENSIONAL KINEMATICS 107
When we speak of the range of a projectile on level ground, we assume that R is very small compared with the circumference of the Earth. If,
however, the range is large, the Earth curves away below the projectile and acceleration of gravity changes direction along the path. The range is
larger than predicted by the range equation given above because the projectile has farther to fall than it would on level ground. (See Figure 3.42.) If
the initial speed is great enough, the projectile goes into orbit. This is called escape velocity. This possibility was recognized centuries before it could
be accomplished. When an object is in orbit, the Earth curves away from underneath the object at the same rate as it falls. The object thus falls
continuously but never hits the surface. These and other aspects of orbital motion, such as the rotation of the Earth, will be covered analytically and in
greater depth later in this text.
Once again we see that thinking about one topic, such as the range of a projectile, can lead us to others, such as the Earth orbits. In Addition of
Velocities, we will examine the addition of velocities, which is another important aspect of two-dimensional kinematics and will also yield insights beyond the immediate topic.
Figure 3.42 Projectile to satellite. In each case shown here, a projectile is launched from a very high tower to avoid air resistance. With increasing initial speed, the range
increases and becomes longer than it would be on level ground because the Earth curves away underneath its path. With a large enough initial speed, orbit is achieved.
PhET Explorations: Projectile Motion
Blast a Buick out of a cannon! Learn about projectile motion by firing various objects. Set the angle, initial speed, and mass. Add air resistance.
Make a game out of this simulation by trying to hit a target.
Figure 3.43 Projectile Motion (http://cnx.org/content/m42042/1.8/projectile-motion_en.jar)
3.5 Addition of Velocities
Relative Velocity
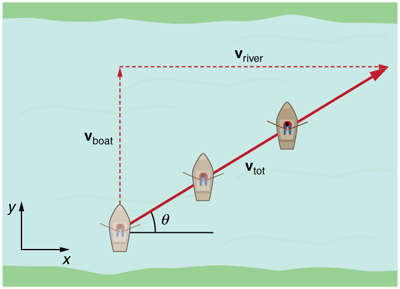
If a person rows a boat across a rapidly flowing river and tries to head directly for the other shore, the boat instead moves diagonally relative to the
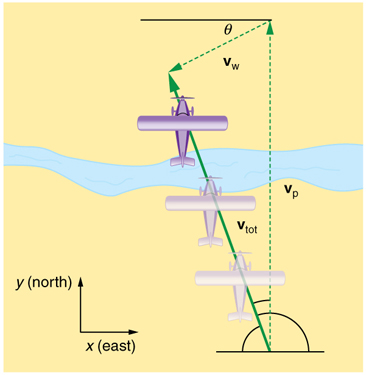
shore, as in Figure 3.44. The boat does not move in the direction in which it is pointed. The reason, of course, is that the river carries the boat downstream. Similarly, if a small airplane flies overhead in a strong crosswind, you can sometimes see that the plane is not moving in the direction in
which it is pointed, as illustrated in Figure 3.45. The plane is moving straight ahead relative to the air, but the movement of the air mass relative to the ground carries it sideways.
108 CHAPTER 3 | TWO-DIMENSIONAL KINEMATICS
Figure 3.44 A boat trying to head straight across a river will actually move diagonally relative to the shore as shown. Its total velocity (solid arrow) relative to the shore is the sum of its velocity relative to the river plus the velocity of the river relative to the shore.
Figure 3.45 An airplane heading straight north is instead carried to the west and slowed down by wind. The plane does not move relative to the ground in the direction it
points; rather, it moves in the direction of its total velocity (solid arrow).
In each of these situations, an object has a velocity relative to a medium (such as a river) and that medium has a velocity relative to an observer on
solid ground. The velocity of the object relative to the observer is the sum of these velocity vectors, as indicated in Figure 3.44 and











