not look any skinnier. This is because the force of gravity is weaker on the Moon. In fact, when people say that they are “losing weight,” they
really mean that they are losing “mass” (which in turn causes them to weigh less).
Take-Home Experiment: Mass and Weight
What do bathroom scales measure? When you stand on a bathroom scale, what happens to the scale? It depresses slightly. The scale contains
springs that compress in proportion to your weight—similar to rubber bands expanding when pulled. The springs provide a measure of your
weight (for an object which is not accelerating). This is a force in newtons (or pounds). In most countries, the measurement is divided by 9.80 to
give a reading in mass units of kilograms. The scale measures weight but is calibrated to provide information about mass. While standing on a
bathroom scale, push down on a table next to you. What happens to the reading? Why? Would your scale measure the same “mass” on Earth as
on the Moon?
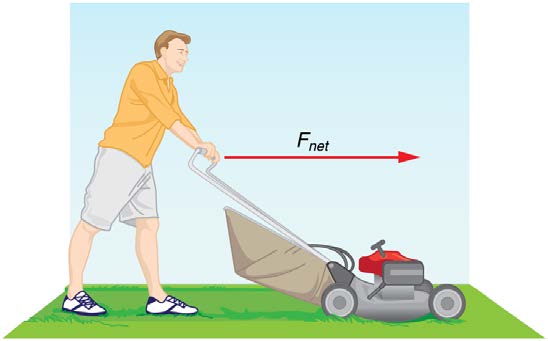
Example 4.1 What Acceleration Can a Person Produce when Pushing a Lawn Mower?
Suppose that the net external force (push minus friction) exerted on a lawn mower is 51 N (about 11 lb) parallel to the ground. The mass of the
mower is 24 kg. What is its acceleration?
130 CHAPTER 4 | DYNAMICS: FORCE AND NEWTON'S LAWS OF MOTION
Figure 4.7 The net force on a lawn mower is 51 N to the right. At what rate does the lawn mower accelerate to the right?
Strategy
Since Fnet and m are given, the acceleration can be calculated directly from Newton’s second law as stated in Fnet = ma .
Solution
The magnitude of the acceleration a is a = F net
m . Entering known values gives
(4.9)
a = 51 N
24 kg
Substituting the units kg ⋅ m/s2 for N yields
(4.10)
a = 51 kg ⋅ m/s2
24 kg
= 2.1 m/s2.
Discussion
The direction of the acceleration is the same direction as that of the net force, which is parallel to the ground. There is no information given in this
example about the individual external forces acting on the system, but we can say something about their relative magnitudes. For example, the
force exerted by the person pushing the mower must be greater than the friction opposing the motion (since we know the mower moves forward),
and the vertical forces must cancel if there is to be no acceleration in the vertical direction (the mower is moving only horizontally). The
acceleration found is small enough to be reasonable for a person pushing a mower. Such an effort would not last too long because the person’s
top speed would soon be reached.
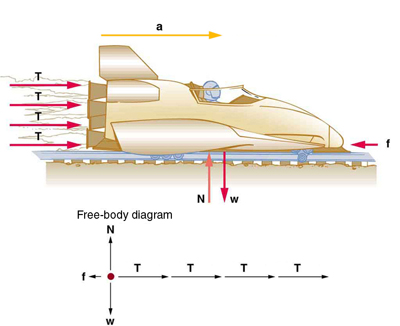
Example 4.2 What Rocket Thrust Accelerates This Sled?
Prior to manned space flights, rocket sleds were used to test aircraft, missile equipment, and physiological effects on human subjects at high
speeds. They consisted of a platform that was mounted on one or two rails and propelled by several rockets. Calculate the magnitude of force
exerted by each rocket, called its thrust T , for the four-rocket propulsion system shown in Figure 4.8. The sled’s initial acceleration is
49 m/s2, the mass of the system is 2100 kg, and the force of friction opposing the motion is known to be 650 N.
CHAPTER 4 | DYNAMICS: FORCE AND NEWTON'S LAWS OF MOTION 131
Figure 4.8 A sled experiences a rocket thrust that accelerates it to the right. Each rocket creates an identical thrust T . As in other situations where there is only
horizontal acceleration, the vertical forces cancel. The ground exerts an upward force N on the system that is equal in magnitude and opposite in direction to its weight,
w . The system here is the sled, its rockets, and rider, so none of the forces between these objects are considered. The arrow representing friction ( f ) is drawn larger than scale.
Strategy
Although there are forces acting vertically and horizontally, we assume the vertical forces cancel since there is no vertical acceleration. This
leaves us with only horizontal forces and a simpler one-dimensional problem. Directions are indicated with plus or minus signs, with right taken
as the positive direction. See the free-body diagram in the figure.
Solution
Since acceleration, mass, and the force of friction are given, we start with Newton’s second law and look for ways to find the thrust of the
engines. Since we have defined the direction of the force and acceleration as acting “to the right,” we need to consider only the magnitudes of
these quantities in the calculations. Hence we begin with
F
(4.11)
net = ma,
where F net is the net force along the horizontal direction. We can see from Figure 4.8 that the engine thrusts add, while friction opposes the thrust. In equation form, the net external force is
F
(4.12)
net = 4 T − f .
Substituting this into Newton’s second law gives
F
(4.13)
net = ma = 4 T − f .
Using a little algebra, we solve for the total thrust 4 T:
(4.14)
4 T = ma + f .
Substituting known values yields
(4.15)
4 T = ma + f = (2100 kg)(49 m/s2 ) + 650 N.
So the total thrust is
(4.16)
4 T = 1.0×105 N,
and the individual thrusts are
(4.17)
T = 1.0×105 N
4
= 2.5×104 N.
Discussion
The numbers are quite large, so the result might surprise you. Experiments such as this were performed in the early 1960s to test the limits of
human endurance and the setup designed to protect human subjects in jet fighter emergency ejections. Speeds of 1000 km/h were obtained,
with accelerations of 45 g 's. (Recall that g , the acceleration due to gravity, is 9.80 m/s2 . When we say that an acceleration is 45 g 's, it is
45 × 9.80 m/s2 , which is approximately 440 m/s2 .) While living subjects are not used any more, land speeds of 10,000 km/h have been
obtained with rocket sleds. In this example, as in the preceding one, the system of interest is obvious. We will see in later examples that
choosing the system of interest is crucial—and the choice is not always obvious.

132 CHAPTER 4 | DYNAMICS: FORCE AND NEWTON'S LAWS OF MOTION
Newton’s second law of motion is more than a definition; it is a relationship among acceleration, force, and mass. It can help us make
predictions. Each of those physical quantities can be defined independently, so the second law tells us something basic and universal about
nature. The next section introduces the third and final law of motion.
4.4 Newton’s Third Law of Motion: Symmetry in Forces
There is a passage in the musical Man of la Mancha that relates to Newton’s third law of motion. Sancho, in describing a fight with his wife to Don
Quixote, says, “Of course I hit her back, Your Grace, but she’s a lot harder than me and you know what they say, ‘Whether the stone hits the pitcher
or the pitcher hits the stone, it’s going to be bad for the pitcher.’” This is exactly what happens whenever one body exerts a force on another—the first
also experiences a force (equal in magnitude and opposite in direction). Numerous common experiences, such as stubbing a toe or throwing a ball,
confirm this. It is precisely stated in Newton’s third law of motion.
Newton’s Third Law of Motion
Whenever one body exerts a force on a second body, the first body experiences a force that is equal in magnitude and opposite in direction to
the force that it exerts.
This law represents a certain symmetry in nature: Forces always occur in pairs, and one body cannot exert a force on another without experiencing a
force itself. We sometimes refer to this law loosely as “action-reaction,” where the force exerted is the action and the force experienced as a
consequence is the reaction. Newton’s third law has practical uses in analyzing the origin of forces and understanding which forces are external to a
system.
We can readily see Newton’s third law at work by taking a look at how people move about. Consider a swimmer pushing off from the side of a pool,
as illustrated in Figure 4.9. She pushes against the pool wall with her feet and accelerates in the direction opposite to that of her push. The wall has exerted an equal and opposite force back on the swimmer. You might think that two equal and opposite forces would cancel, but they do not because
they act on different systems. In this case, there are two systems that we could investigate: the swimmer or the wall. If we select the swimmer to be
the system of interest, as in the figure, then Fwall on feet is an external force on this system and affects its motion. The swimmer moves in the
direction of Fwall on feet . In contrast, the force Ffeet on wall acts on the wall and not on our system of interest. Thus Ffeet on wall does not directly
affect the motion of the system and does not cancel Fwall on feet . Note that the swimmer pushes in the direction opposite to that in which she wishes
to move. The reaction to her push is thus in the desired direction.
Figure 4.9 When the swimmer exerts a force Ffeet on wall on the wall, she accelerates in the direction opposite to that of her push. This means the net external force on her is in the direction opposite to Ffeet on wall . This opposition occurs because, in accordance with Newton’s third law of motion, the wall exerts a force Fwall on feet on her, equal in magnitude but in the direction opposite to the one she exerts on it. The line around the swimmer indicates the system of interest. Note that Ffeet on wall does not
act on this system (the swimmer) and, thus, does not cancel Fwall on feet . Thus the free-body diagram shows only Fwall on feet , w , the gravitational force, and BF , the buoyant force of the water supporting the swimmer’s weight. The vertical forces w and BF cancel since there is no vertical motion.
Other examples of Newton’s third law are easy to find. As a professor paces in front of a whiteboard, she exerts a force backward on the floor. The
floor exerts a reaction force forward on the professor that causes her to accelerate forward. Similarly, a car accelerates because the ground pushes
forward on the drive wheels in reaction to the drive wheels pushing backward on the ground. You can see evidence of the wheels pushing backward
when tires spin on a gravel road and throw rocks backward. In another example, rockets move forward by expelling gas backward at high velocity.
This means the rocket exerts a large backward force on the gas in the rocket combustion chamber, and the gas therefore exerts a large reaction
force forward on the rocket. This reaction force is called thrust. It is a common misconception that rockets propel themselves by pushing on the
ground or on the air behind them. They actually work better in a vacuum, where they can more readily expel the exhaust gases. Helicopters similarly
create lift by pushing air down, thereby experiencing an upward reaction force. Birds and airplanes also fly by exerting force on air in a direction
opposite to that of whatever force they need. For example, the wings of a bird force air downward and backward in order to get lift and move forward.
An octopus propels itself in the water by ejecting water through a funnel from its body, similar to a jet ski. In a situation similar to Sancho’s,
professional cage fighters experience reaction forces when they punch, sometimes breaking their hand by hitting an opponent’s body.
CHAPTER 4 | DYNAMICS: FORCE AND NEWTON'S LAWS OF MOTION 133
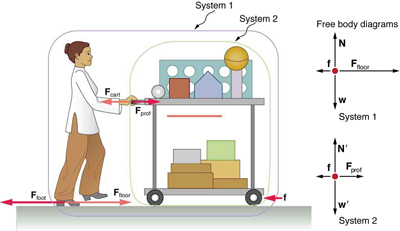
Example 4.3 Getting Up To Speed: Choosing the Correct System
A physics professor pushes a cart of demonstration equipment to a lecture hall, as seen in Figure 4.10. Her mass is 65.0 kg, the cart’s is 12.0
kg, and the equipment’s is 7.0 kg. Calculate the acceleration produced when the professor exerts a backward force of 150 N on the floor. All
forces opposing the motion, such as friction on the cart’s wheels and air resistance, total 24.0 N.
Figure 4.10 A professor pushes a cart of demonstration equipment. The lengths of the arrows are proportional to the magnitudes of the forces (except for f , since it is
too small to draw to scale). Different questions are asked in each example; thus, the system of interest must be defined differently for each. System 1 is appropriate for
Example 4.4, since it asks for the acceleration of the entire group of objects. Only Ffloor and f are external forces acting on System 1 along the line of motion. All other forces either cancel or act on the outside world. System 2 is chosen for this example so that Fprof will be an external force and enter into Newton’s second law.
Note that the free-body diagrams, which allow us to apply Newton’s second law, vary with the system chosen.
Strategy
Since they accelerate as a unit, we define the system to be the professor, cart, and equipment. This is System 1 in Figure 4.10. The professor
pushes backward with a force Ffoot of 150 N. According to Newton’s third law, the floor exerts a forward reaction force Ffloor of 150 N on
System 1. Because all motion is horizontal, we can assume there is no net force in the vertical direction. The problem is therefore one-
dimensional along the horizontal direction. As noted, f opposes the motion and is thus in the opposite direction of Ffloor . Note that we do not
include the forces Fprof or Fcart because these are internal forces, and we do not include Ffoot because it acts on the floor, not on the
system. There are no other significant forces acting on System 1. If the net external force can be found from all this information, we can use
Newton’s second law to find the acceleration as requested. See the free-body diagram in the figure.
Solution
Newton’s second law is given by
(4.18)
a = F net
m .
The net external force on System 1 is deduced from Figure 4.10 and the discussion above to be
F
(4.19)
net = F floor − f = 150 N − 24.0 N = 126 N.
The mass of System 1 is
m
(4.20)
= (65.0 + 12.0 + 7.0) kg = 84 kg.
These values of F net and m produce an acceleration of
(4.21)
a = F net
m ,
a = 126 N
84 kg = 1.5 m/s2 .
Discussion
None of the forces between components of System 1, such as between the professor’s hands and the cart, contribute to the net external force
because they are internal to System 1. Another way to look at this is to note that forces between components of a system cancel because they
are equal in magnitude and opposite in direction. For example, the force exerted by the professor on the cart results in an equal and opposite
force back on her. In this case both forces act on the same system and, therefore, cancel. Thus internal forces (between components of a
system) cancel. Choosing System 1 was crucial to solving this problem.

134 CHAPTER 4 | DYNAMICS: FORCE AND NEWTON'S LAWS OF MOTION
Example 4.4 Force on the Cart—Choosing a New System
Calculate the force the professor exerts on the cart in Figure 4.10 using data from the previous example if needed.
Strategy
If we now define the system of interest to be the cart plus equipment (System 2 in Figure 4.10), then the net external force on System 2 is the
force the professor exerts on the cart minus friction. The force she exerts on the cart, Fprof , is an external force acting on System 2. Fprof
was internal to System 1, but it is external to System 2 and will enter Newton’s second law for System 2.
Solution
Newton’s second law can be used to find Fprof . Starting with
(4.22)
a = F net
m
and noting that the magnitude of the net external force on System 2 is
F
(4.23)
net = F prof − f ,
we solve for F prof , the desired quantity:
F
(4.24)
prof = F net + f .
The value of f is given, so we must calculate net F net . That can be done since both the acceleration and mass of System 2 are known. Using
Newton’s second law we see that
F
(4.25)
net = ma,
where the mass of System 2 is 19.0 kg ( m = 12.0 kg + 7.0 kg) and its acceleration was found to be a = 1.5 m/s2 in the previous example.
Thus,
F
(4.26)
net = ma,
(4.27)
F net = (19.0 kg)(1.5 m/s2) = 29 N.
Now we can find the desired force:
F
(4.28)
prof = F net + f ,
F
(4.29)
prof = 29 N+24.0 N = 53 N.
Discussion
It is interesting that this force is significantly less than the 150-N force the professor exerted backward on the floor. Not all of that 150-N force is
transmitted to the cart; some of it accelerates the professor.
The choice of a system is an important analytical step both in solving problems and in thoroughly understanding the physics of the situation
(which is not necessarily the same thing).
PhET Explorations: Gravity Force Lab
Visualize the gravitational force that two objects exert on each other. Change properties of the objects in order to see how it changes the gravity
force.
Figure 4.11 Gravity Force Lab (http://cnx.org/content/m42074/1.3/gravity-force-lab_en.jar)
4.5 Normal, Tension, and Other Examples of Forces
Forces are given many names, such as push, pull, thrust, lift, weight, friction, and tension. Traditionally, forces have been grouped into several
categories and given names relating to their source, how they are transmitted, or their effects. The most important of these categories are discussed
in this section, together with some interesting applications. Further examples of forces are discussed later in this text.
Normal Force
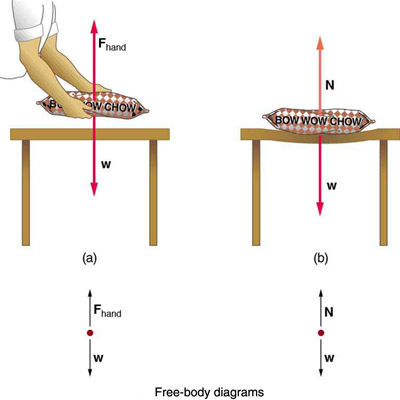
Weight (also called force of gravity) is a pervasive force that acts at all times and must be counteracted to keep an object from falling. You definitely
notice that you must support the weight of a heavy object by pushing up on it when you hold it stationary, as illustrated in Figure 4.12(a). But how do
CHAPTER 4 | DYNAMICS: FORCE AND NEWTON'S LAWS OF MOTION 135
inanimate objects like a table support the weight of a mass placed on them, such as shown in Figure 4.12(b)? When the bag of dog food is placed on
the table, the table actually sags slightly under the load. This would be noticeable if the load were placed on a card table, but even rigid objects
deform when a force is applied to them. Unless the object is deformed beyond its limit, it will exert a restoring force much like a deformed spring (or
trampoline or diving board). The greater the deformation, the greater the restoring force. So when the load is placed on the table, the table sags until
the restoring force becomes as large as the weight of the load. At this point the net external force on the load is zero. That is the situation when the
load is stationary on the table. The table sags quickly, and the sag is slight so we do not notice it. But it is similar to the sagging of a trampoline when
you climb onto it.
Figure 4.12 (a) The person holding the bag of dog food must supply an upward force Fhand equal in magnitude and opposite in direction to the weight of the food w . (b) The card table sags when the dog food is placed on it, much like a stiff trampoline. Elastic restoring forces in the table grow as it sags until they supply a force N equal in
magnitude and opposite in direction to the weight of the load.
We must conclude that whatever supports a load, be it animate or not, must supply an upward force equal to the weight of the load, as we assumed
in a few of the previous examples. If the force supporting a load is perpendicular to the surface of contact between the load and its support, this force
is defined to be a normal force and here is given the symbol N . (This is not the unit for force N.) The word normal means perpendicular to a
surface. The normal force can be less than the object’s weight if the object is on an incline, as you will see in the next example.
Common Misconception: Normal Force (N) vs. Newton (N)
In this section we have introduced the quantity normal force, which is represented by the variable N . This should not be confused with the
symbol for the newton, which is also represented by the letter N. These symbols are particularly important to distinguish because the units of a
normal force ( N ) happen to be newtons (N). For example, the normal force N that the floor exerts on a chair might be N = 100 N . One
important difference is that normal force is a vector, while the newton is simply a unit. Be careful not to confuse these letters in your calculations!
You will encounter more similarities among variables and units as you proceed in physics. Another example of this is the quantity work ( W ) and
the unit watts (W).
Example 4.5 Weight on an Incline, a Two-Dimensional Problem
Consider the skier on a slope shown in Figure 4.13. Her mass including equipment is 60.0 kg. (a) What is her acceleration if friction is
negligible? (b) What is her acceleration if friction is known to be 45.0 N?
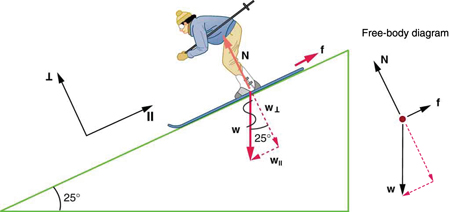
136 CHAPTER 4 | DYNAMICS: FORCE AND NEWTON'S LAWS OF MOTION
Figure 4.13 Since motion and friction are parallel to the slope, it is most convenient to project all forces onto a coordinate system where one axis is parallel to the slope
and the other is perpendicular (axes shown to left of skier). N is perpendicular to the slope and f is parallel to the slope, but w has components along both axes, namely w⊥ and w ∥ . N is equal in magnitude to w⊥ , so that there is no motion perpendicular to the slope, but f is less than w ∥ , so that there is a downslope acceleration (along the parallel axis).
Strategy
This is a two-dimensional problem, since the forces on the skier (the system of interest) are not parallel. The approach we have used in two-
dimensional kinematics also works very well here. Choo










