The bodies we are dealing with tend to be large. To simplify the situation we assume that the body acts as if its entire mass is concentrated at one
specific point called the center of mass (CM), which will be further explored in Linear Momentum and Collisions. For two bodies having masses
m and M with a distance r between their centers of mass, the equation for Newton’s universal law of gravitation is
(6.40)
F = GmM
r 2 ,
CHAPTER 6 | UNIFORM CIRCULAR MOTION AND GRAVITATION 201
where F is the magnitude of the gravitational force and G is a proportionality factor called the gravitational constant. G is a universal
gravitational constant—that is, it is thought to be the same everywhere in the universe. It has been measured experimentally to be
(6.41)
G = 6.673×10−11N ⋅ m2
kg2
in SI units. Note that the units of G are such that a force in newtons is obtained from F = GmM
r 2 , when considering masses in kilograms and
distance in meters. For example, two 1.000 kg masses separated by 1.000 m will experience a gravitational attraction of 6.673×10−11 N . This is
an extraordinarily small force. The small magnitude of the gravitational force is consistent with everyday experience. We are unaware that even large
objects like mountains exert gravitational forces on us. In fact, our body weight is the force of attraction of the entire Earth on us with a mass of
6×1024 kg .
Recall that the acceleration due to gravity g is about 9.80 m/s2 on Earth. We can now determine why this is so. The weight of an object mg is the
gravitational force between it and Earth. Substituting mg for F in Newton’s universal law of gravitation gives
(6.42)
mg = GmM
r 2 ,
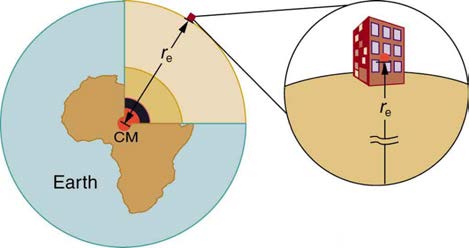
where m is the mass of the object, M is the mass of Earth, and r is the distance to the center of Earth (the distance between the centers of mass
of the object and Earth). See Figure 6.22. The mass m of the object cancels, leaving an equation for g :
(6.43)
g = GM
r 2.
Substituting known values for Earth’s mass and radius (to three significant figures),
⎛
⎞
(6.44)
g = ⎜6.67×10−11N ⋅ m2⎟× 5.98×1024 kg
⎝
kg2 ⎠ (6.38×106 m)2,
and we obtain a value for the acceleration of a falling body:
(6.45)
g = 9.80 m/s2.
Figure 6.22 The distance between the centers of mass of Earth and an object on its surface is very nearly the same as the radius of Earth, because Earth is so much larger
than the object.
This is the expected value and is independent of the body’s mass. Newton’s law of gravitation takes Galileo’s observation that all masses fall with the
same acceleration a step further, explaining the observation in terms of a force that causes objects to fall—in fact, in terms of a universally existing
force of attraction between masses.
Take-Home Experiment
Take a marble, a ball, and a spoon and drop them from the same height. Do they hit the floor at the same time? If you drop a piece of paper as
well, does it behave like the other objects? Explain your observations.
Making Connections
Attempts are still being made to understand the gravitational force. As we shall see in Particle Physics, modern physics is exploring the
connections of gravity to other forces, space, and time. General relativity alters our view of gravitation, leading us to think of gravitation as
bending space and time.
In the following example, we make a comparison similar to one made by Newton himself. He noted that if the gravitational force caused the Moon to
orbit Earth, then the acceleration due to gravity should equal the centripetal acceleration of the Moon in its orbit. Newton found that the two
accelerations agreed “pretty nearly.”
202 CHAPTER 6 | UNIFORM CIRCULAR MOTION AND GRAVITATION
Example 6.6 Earth’s Gravitational Force Is the Centripetal Force Making the Moon Move in a Curved Path
(a) Find the acceleration due to Earth’s gravity at the distance of the Moon.
(b) Calculate the centripetal acceleration needed to keep the Moon in its orbit (assuming a circular orbit about a fixed Earth), and compare it with
the value of the acceleration due to Earth’s gravity that you have just found.
Strategy for (a)
This calculation is the same as the one finding the acceleration due to gravity at Earth’s surface, except that r is the distance from the center of
Earth to the center of the Moon. The radius of the Moon’s nearly circular orbit is 3.84×108 m .
Solution for (a)
Substituting known values into the expression for g found above, remembering that M is the mass of Earth not the Moon, yields
⎛
⎞
(6.46)
g = GM ⎜6.67×10−11N ⋅ m2⎟× 5.98×1024 kg
r 2 = ⎝
kg2 ⎠ (3.84×108 m)2
= 2.70×10−3 m/s.2
Strategy for (b)
Centripetal acceleration can be calculated using either form of
(6.47)
⎫
ac = v 2 r ⎬.
a
⎭
c = rω 2
We choose to use the second form:
(6.48)
ac = rω 2,
where ω is the angular velocity of the Moon about Earth.
Solution for (b)
Given that the period (the time it takes to make one complete rotation) of the Moon’s orbit is 27.3 days, (d) and using
(6.49)
1 d×24hrd×60min
hr ×60 s
min = 86,400 s
we see that
(6.50)
ω = Δ θ
Δ t =
2π rad
(27.3 d)(86,400 s/d) = 2.66×10−6rad
s .
The centripetal acceleration is
(6.51)
ac = rω 2 = (3.84×108 m)(2.66×10−6 rad/s)2
= 2.72×10−3 m/s.2
The direction of the acceleration is toward the center of the Earth.
Discussion
The centripetal acceleration of the Moon found in (b) differs by less than 1% from the acceleration due to Earth’s gravity found in (a). This
agreement is approximate because the Moon’s orbit is slightly elliptical, and Earth is not stationary (rather the Earth-Moon system rotates about
its center of mass, which is located some 1700 km below Earth’s surface). The clear implication is that Earth’s gravitational force causes the
Moon to orbit Earth.
Why does Earth not remain stationary as the Moon orbits it? This is because, as expected from Newton’s third law, if Earth exerts a force on the
Moon, then the Moon should exert an equal and opposite force on Earth (see Figure 6.23). We do not sense the Moon’s effect on Earth’s motion,
because the Moon’s gravity moves our bodies right along with Earth but there are other signs on Earth that clearly show the effect of the Moon’s
gravitational force as discussed in Satellites and Kepler's Laws: An Argument for Simplicity.

CHAPTER 6 | UNIFORM CIRCULAR MOTION AND GRAVITATION 203
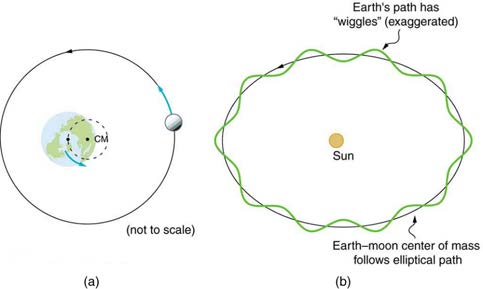
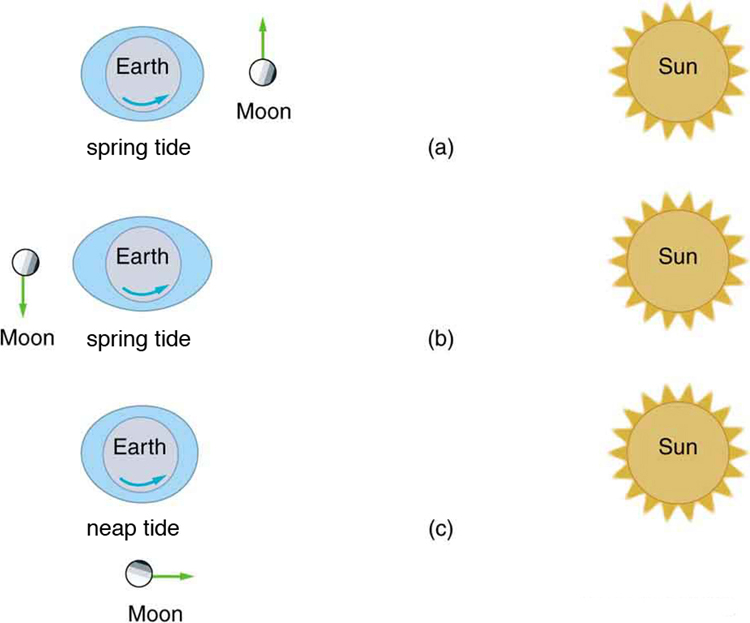
Figure 6.23 (a) Earth and the Moon rotate approximately once a month around their common center of mass. (b) Their center of mass orbits the Sun in an elliptical orbit, but
Earth’s path around the Sun has “wiggles” in it. Similar wiggles in the paths of stars have been observed and are considered direct evidence of planets orbiting those stars.
This is important because the planets’ reflected light is often too dim to be observed.
Tides
Ocean tides are one very observable result of the Moon’s gravity acting on Earth. Figure 6.24 is a simplified drawing of the Moon’s position relative to the tides. Because water easily flows on Earth’s surface, a high tide is created on the side of Earth nearest to the Moon, where the Moon’s
gravitational pull is strongest. Why is there also a high tide on the opposite side of Earth? The answer is that Earth is pulled toward the Moon more
than the water on the far side, because Earth is closer to the Moon. So the water on the side of Earth closest to the Moon is pulled away from Earth,
and Earth is pulled away from water on the far side. As Earth rotates, the tidal bulge (an effect of the tidal forces between an orbiting natural satellite
and the primary planet that it orbits) keeps its orientation with the Moon. Thus there are two tides per day (the actual tidal period is about 12 hours
and 25.2 minutes), because the Moon moves in its orbit each day as well).
Figure 6.24 The Moon causes ocean tides by attracting the water on the near side more than Earth, and by attracting Earth more than the water on the far side. The distances
and sizes are not to scale. For this simplified representation of the Earth-Moon system, there are two high and two low tides per day at any location, because Earth rotates
under the tidal bulge.
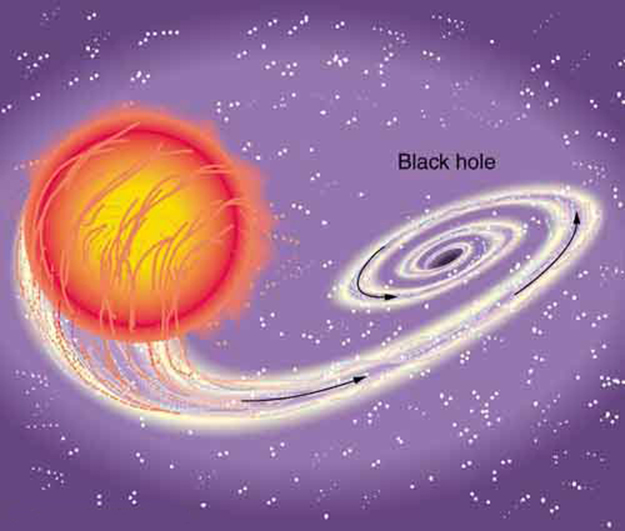
The Sun also affects tides, although it has about half the effect of the Moon. However, the largest tides, called spring tides, occur when Earth, the
Moon, and the Sun are aligned. The smallest tides, called neap tides, occur when the Sun is at a 90º angle to the Earth-Moon alignment.
Figure 6.25 (a, b) Spring tides: The highest tides occur when Earth, the Moon, and the Sun are aligned. (c)Neap tide: The lowest tides occur when the Sun lies at 90º to the
Earth-Moon alignment. Note that this figure is not drawn to scale.

204 CHAPTER 6 | UNIFORM CIRCULAR MOTION AND GRAVITATION
Tides are not unique to Earth but occur in many astronomical systems. The most extreme tides occur where the gravitational force is the strongest
and varies most rapidly, such as near black holes (see Figure 6.26). A few likely candidates for black holes have been observed in our galaxy. These have masses greater than the Sun but have diameters only a few kilometers across. The tidal forces near them are so great that they can actually
tear matter from a companion star.
Figure 6.26 A black hole is an object with such strong gravity that not even light can escape it. This black hole was created by the supernova of one star in a two-star system.
The tidal forces created by the black hole are so great that it tears matter from the companion star. This matter is compressed and heated as it is sucked into the black hole,
creating light and X-rays observable from Earth.
”Weightlessness” and Microgravity
In contrast to the tremendous gravitational force near black holes is the apparent gravitational field experienced by astronauts orbiting Earth. What is
the effect of “weightlessness” upon an astronaut who is in orbit for months? Or what about the effect of weightlessness upon plant growth?
Weightlessness doesn’t mean that an astronaut is not being acted upon by the gravitational force. There is no “zero gravity” in an astronaut’s orbit.
The term just means that the astronaut is in free-fall, accelerating with the acceleration due to gravity. If an elevator cable breaks, the passengers
inside will be in free fall and will experience weightlessness. You can experience short periods of weightlessness in some rides in amusement parks.
Figure 6.27 Astronauts experiencing weightlessness on board the International Space Station. (credit: NASA)
Microgravity refers to an environment in which the apparent net acceleration of a body is small compared with that produced by Earth at its surface.
Many interesting biology and physics topics have been studied over the past three decades in the presence of microgravity. Of immediate concern is
the effect on astronauts of extended times in outer space, such as at the International Space Station. Researchers have observed that muscles will
atrophy (waste away) in this environment. There is also a corresponding loss of bone mass. Study continues on cardiovascular adaptation to space
flight. On Earth, blood pressure is usually higher in the feet than in the head, because the higher column of blood exerts a downward force on it, due
to gravity. When standing, 70% of your blood is below the level of the heart, while in a horizontal position, just the opposite occurs. What difference
does the absence of this pressure differential have upon the heart?
Some findings in human physiology in space can be clinically important to the management of diseases back on Earth. On a somewhat negative
note, spaceflight is known to affect the human immune system, possibly making the crew members more vulnerable to infectious diseases.
Experiments flown in space also have shown that some bacteria grow faster in microgravity than they do on Earth. However, on a positive note,
studies indicate that microbial antibiotic production can increase by a factor of two in space-grown cultures. One hopes to be able to understand
these mechanisms so that similar successes can be achieved on the ground. In another area of physics space research, inorganic crystals and
protein crystals have been grown in outer space that have much higher quality than any grown on Earth, so crystallography studies on their structure
can yield much better results.
Plants have evolved with the stimulus of gravity and with gravity sensors. Roots grow downward and shoots grow upward. Plants might be able to
provide a life support system for long duration space missions by regenerating the atmosphere, purifying water, and producing food. Some studies
have indicated that plant growth and development are not affected by gravity, but there is still uncertainty about structural changes in plants grown in
a microgravity environment.
CHAPTER 6 | UNIFORM CIRCULAR MOTION AND GRAVITATION 205
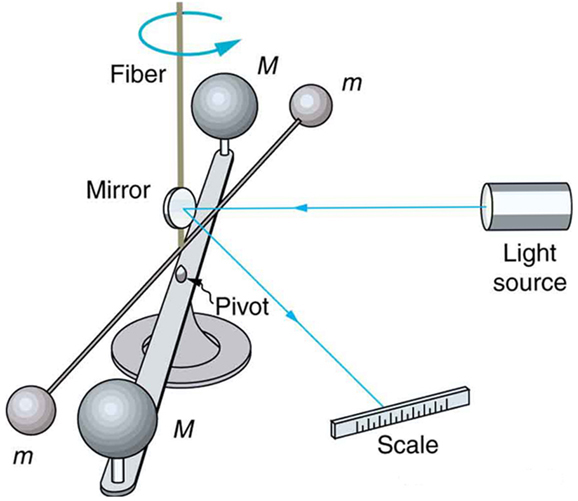
The Cavendish Experiment: Then and Now
As previously noted, the universal gravitational constant G is determined experimentally. This definition was first done accurately by Henry
Cavendish (1731–1810), an English scientist, in 1798, more than 100 years after Newton published his universal law of gravitation. The
measurement of G is very basic and important because it determines the strength of one of the four forces in nature. Cavendish’s experiment was
very difficult because he measured the tiny gravitational attraction between two ordinary-sized masses (tens of kilograms at most), using apparatus
like that in Figure 6.28. Remarkably, his value for G differs by less than 1% from the best modern value.
One important consequence of knowing G was that an accurate value for Earth’s mass could finally be obtained. This was done by measuring the
acceleration due to gravity as accurately as possible and then calculating the mass of Earth M from the relationship Newton’s universal law of
gravitation gives
(6.52)
mg = GmM
r 2 ,
where m is the mass of the object, M is the mass of Earth, and r is the distance to the center of Earth (the distance between the centers of mass
of the object and Earth). See Figure 6.21. The mass m of the object cancels, leaving an equation for g :
(6.53)
g = GM
r 2.
Rearranging to solve for M yields
(6.54)
M = gr 2
G .
So M can be calculated because all quantities on the right, including the radius of Earth r , are known from direct measurements. We shall see in
Satellites and Kepler's Laws: An Argument for Simplicity that knowing G also allows for the determination of astronomical masses. Interestingly, of all the fundamental constants in physics, G is by far the least well determined.
The Cavendish experiment is also used to explore other aspects of gravity. One of the most interesting questions is whether the gravitational force
depends on substance as well as mass—for example, whether one kilogram of lead exerts the same gravitational pull as one kilogram of water. A
Hungarian scientist named Roland von Eötvös pioneered this inquiry early in the 20th century. He found, with an accuracy of five parts per billion, that
the gravitational force does not depend on the substance. Such experiments continue today, and have improved upon Eötvös’ measurements.
Cavendish-type experiments such as those of Eric Adelberger and others at the University of Washington, have also put severe limits on the
possibility of a fifth force and have verified a major prediction of general relativity—that gravitational energy contributes to rest mass. Ongoing
measurements there use a torsion balance and a parallel plate (not spheres, as Cavendish used) to examine how Newton’s law of gravitation works
over sub-millimeter distances. On this small-scale, do gravitational effects depart from the inverse square law? So far, no deviation has been
observed.
Figure 6.28 Cavendish used an apparatus like this to measure the gravitational attraction between the two suspended spheres ( m ) and the two on the stand ( M ) by observing the amount of torsion (twisting) created in the fiber. Distance between the masses can be varied to check the dependence of the force on distance. Modern
experiments of this type continue to explore gravity.
6.6 Satellites and Kepler’s Laws: An Argument for Simplicity
Examples of gravitational orbits abound. Hundreds of artificial satellites orbit Earth together with thousands of pieces of debris. The Moon’s orbit
about Earth has intrigued humans from time immemorial. The orbits of planets, asteroids, meteors, and comets about the Sun are no less interesting.
If we look further, we see almost unimaginable numbers of stars, galaxies, and other celestial objects orbiting one another and interacting through
gravity.
All these motions are governed by gravitational force, and it is possible to describe them to various degrees of precision. Precise descriptions of
complex systems must be made with large computers. However, we can describe an important class of orbits without the use of computers, and we
shall find it instructive to study them. These orbits have the following characteristics:
206 CHAPTER 6 | UNIFORM CIRCULAR MOTION AND GRAVITATION
1. A small mass m orbits a much larger mass M . This allows us to view the motion as if M were stationary—in fact, as if from an inertial frame
of reference placed on M —without significant error. Mass m is the satellite of M , if the orbit is gravitationally bound.
2. The system is isolated from other masses. This allows us to neglect any small effects due to outside masses.
The conditions are satisfied, to good approximation, by Earth’s satellites (including the Moon), by objects orbiting the Sun, and by the satellites of
other planets. Historically, planets were studied first, and there is a classical set of three laws, called Kepler’s laws of planetary motion, that describe
the orbits of all bodies satisfying the two previous conditions (not just planets in our solar system). These descriptive laws are named for the German
astronomer Johannes Kepler (1571–1630), who devised them after careful study (over some 20 years) of a large amount of meticulously recorded
observations of planetary motion done by Tycho Brahe (1546–1601). Such careful collection and detailed recording of methods and data are
hallmarks of good science. Data constitute the evidence from which new interpretations and meanings can be constructed.
Kepler’s Laws of Planetary Motion
Kepler’s First Law
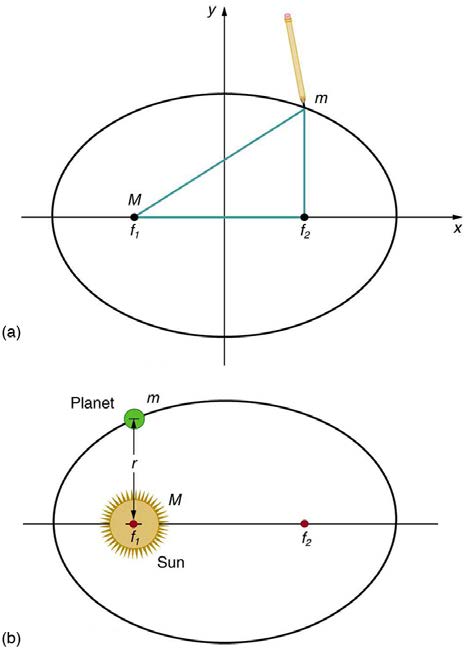
The orbit of each planet about the Sun is an ellipse with the Sun at one focus.
Figure 6.29 (a) An ellipse is a closed curve such that the sum of the distances from a point on the curve to the two foci ( f 1 and f 2 ) is a constant. You can draw an ellipse as shown by putting a pin at each focus, and then placing a string around a pencil and the pins and tracing a line on paper. A circle is a special case of an ellipse in which the
two foci coincide (thus any point on the circle is the same distance from the center). (b) For any closed gravitational orbit, m follows an elliptical path with M at one focus.
Kepler’s first law states this fact for planets orbiting the Sun.
Kepler’s Second Law
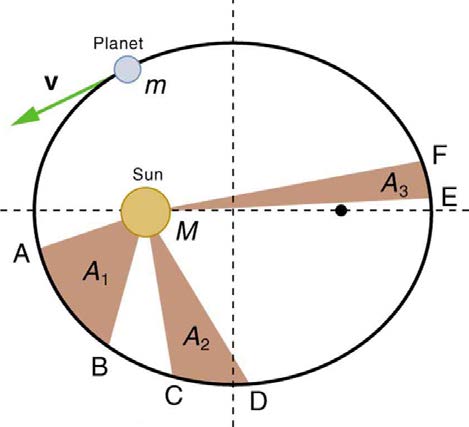
Each planet moves so that an imaginary line drawn from the Sun to the planet sweeps out equal areas in equal times (see Figure 6.30).
Kepler’s Third Law
The ratio of the squares of the periods of any two planets about the Sun is equal to the ratio of the cubes of their average distances from the Sun. In
equation form, this is
2
3
(6.55)
T 1
T 2 = r 1 3,
2
r 2
where T is the period (time for one orbit) and r is the average radius. This equation is valid only for comparing two small masses orbiting the same
large one. Most importantly, this is a descriptive equation only, giving no information as to the cause of the equality.
CHAPTER 6 | UNIFORM CIRCULAR MOTION AND GRAVITATION 207
Figure 6.30 The shaded regions have equal areas. It takes equal times for m to go from A to B, from C to D, and from E to F. The mass m moves fastest when it is closest to M . Kepler’s second law was originally devised for planets orbiting the Sun, but it has broader validity.
Note again that while, for historical reasons, Kepler’s laws are stated for planets orbiting the Sun, they are actually valid for all bodies satisfying the
two previously stated conditions.
Example 6.7 Find the Time for One Orbit of an Earth Satellite
Given that the Moon orbits Earth each 27.3 d and that it is an average distance of 3.84×108 m from the center of Earth, calculate the period of
an artificial satellite orbiting at an average altitude of 1500 km above Earth’s surface.
Strategy
T 2
3
The period, or time for one orbit, is related to the radius of the orbit by Kepler’s third law, given in mathematical form in
1
T 2 = r 1 3 . Let us use
2
r 2
the subscript 1 for the Moon and the subscript 2 for the satellite. We are asked to find T 2 . The given information tells us that the orbital radius of
the Moon is r 1 = 3.84×108 m , and that the period of the Moon is T 1 = 27.3 d . The height of the artificial satellite above Earth’s surface is
given, and so we must add the radius of Earth (6380 km) to get r 2 = (1500 + 6380) km = 7880 km . Now all quantities are known, and so
T 2 can be found.
Solution
Kepler’s third law is
2
3
(6.56)
T 1
T 2 = r 1 3.
2












