This result is the basis for defining the units used to measure rotation angles, Δ θ to be radians (rad), defined so that
(6.3)
2π rad = 1 revolution.
A comparison of some useful angles expressed in both degrees and radians is shown in Table 6.1.
Table 6.1 Comparison of Angular Units
Degree Measures
Radian Measure
30º
π 6
60º
π 3
90º
π 2
120º
2π
3
135º
3π
4
180º
π
Figure 6.4 Points 1 and 2 rotate through the same angle ( Δ θ ), but point 2 moves through a greater arc length (Δ s) because it is at a greater distance from the center of rotation ( r) .
If Δ θ = 2 π rad, then the CD has made one complete revolution, and every point on the CD is back at its original position. Because there are 360º
in a circle or one revolution, the relationship between radians and degrees is thus
(6.4)
2 π rad = 360º
so that
(6.5)
1 rad = 360º
2π = 57.3º.
Angular Velocity
How fast is an object rotating? We define angular velocity ω as the rate of change of an angle. In symbols, this is
(6.6)
ω = Δ θ
Δ t ,
where an angular rotation Δ θ takes place in a time Δ t . The greater the rotation angle in a given amount of time, the greater the angular velocity.
The units for angular velocity are radians per second (rad/s).
Angular velocity ω is analogous to linear velocity v . To get the precise relationship between angular and linear velocity, we again consider a pit on
the rotating CD. This pit moves an arc length Δ s in a time Δ t , and so it has a linear velocity
(6.7)
v = Δ s
Δ t.
188 CHAPTER 6 | UNIFORM CIRCULAR MOTION AND GRAVITATION
From Δ θ = Δ s
r we see that Δ s = rΔ θ . Substituting this into the expression for v gives
(6.8)
v = rΔ θ
Δ t = rω.
We write this relationship in two different ways and gain two different insights:
(6.9)
v = rω or ω = vr.
The first relationship in v = rω or ω = vr states that the linear velocity v is proportional to the distance from the center of rotation, thus, it is largest for a point on the rim (largest r ), as you might expect. We can also call this linear speed v of a point on the rim the tangential speed. The second
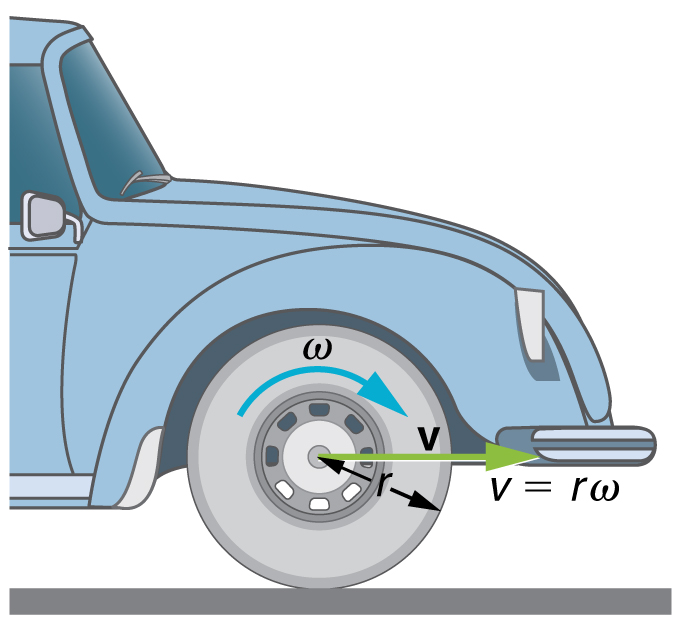
relationship in v = rω or ω = vr can be illustrated by considering the tire of a moving car. Note that the speed of a point on the rim of the tire is the same as the speed v of the car. See Figure 6.5. So the faster the car moves, the faster the tire spins—large v means a large ω , because v = rω . Similarly, a larger-radius tire rotating at the same angular velocity ( ω ) will produce a greater linear speed ( v ) for the car.
Figure 6.5 A car moving at a velocity v to the right has a tire rotating with an angular velocity ω .The speed of the tread of the tire relative to the axle is v , the same as if the car were jacked up. Thus the car moves forward at linear velocity v = rω , where r is the tire radius. A larger angular velocity for the tire means a greater velocity for the car.
Example 6.1 How Fast Does a Car Tire Spin?
Calculate the angular velocity of a 0.300 m radius car tire when the car travels at 15.0 m/s (about 54 km/h ). See Figure 6.5.
Strategy
Because the linear speed of the tire rim is the same as the speed of the car, we have v = 15.0 m/s. The radius of the tire is given to be
r = 0.300 m. Knowing v and r , we can use the second relationship in v = rω, ω = vr to calculate the angular velocity.
Solution
To calculate the angular velocity, we will use the following relationship:
(6.10)
ω = vr.
Substituting the knowns,
(6.11)
ω = 15.0 m/s
0.300 m = 50.0 rad/s.
Discussion
When we cancel units in the above calculation, we get 50.0/s. But the angular velocity must have units of rad/s. Because radians are actually
unitless (radians are defined as a ratio of distance), we can simply insert them into the answer for the angular velocity. Also note that if an earth
mover with much larger tires, say 1.20 m in radius, were moving at the same speed of 15.0 m/s, its tires would rotate more slowly. They would
have an angular velocity
ω
(6.12)
= (15.0 m/s) / (1.20 m) = 12.5 rad/s.
Both ω and v have directions (hence they are angular and linear velocities, respectively). Angular velocity has only two directions with respect to
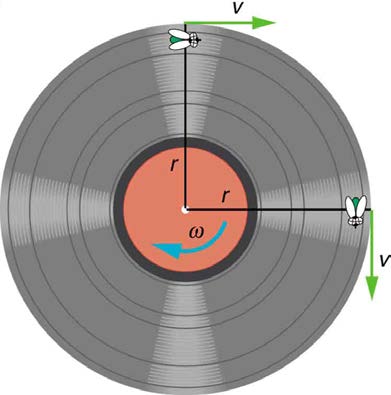
the axis of rotation—it is either clockwise or counterclockwise. Linear velocity is tangent to the path, as illustrated in Figure 6.6.

CHAPTER 6 | UNIFORM CIRCULAR MOTION AND GRAVITATION 189
Take-Home Experiment
Tie an object to the end of a string and swing it around in a horizontal circle above your head (swing at your wrist). Maintain uniform speed as the
object swings and measure the angular velocity of the motion. What is the approximate speed of the object? Identify a point close to your hand
and take appropriate measurements to calculate the linear speed at this point. Identify other circular motions and measure their angular
velocities.
Figure 6.6 As an object moves in a circle, here a fly on the edge of an old-fashioned vinyl record, its instantaneous velocity is always tangent to the circle. The direction of the angular velocity is clockwise in this case.
PhET Explorations: Ladybug Revolution
Figure 6.7 Ladybug Revolution (http://cnx.org/content/m42083/1.4/rotation_en.jar)
Join the ladybug in an exploration of rotational motion. Rotate the merry-go-round to change its angle, or choose a constant angular velocity or
angular acceleration. Explore how circular motion relates to the bug's x,y position, velocity, and acceleration using vectors or graphs.
6.2 Centripetal Acceleration
We know from kinematics that acceleration is a change in velocity, either in its magnitude or in its direction, or both. In uniform circular motion, the
direction of the velocity changes constantly, so there is always an associated acceleration, even though the magnitude of the velocity might be
constant. You experience this acceleration yourself when you turn a corner in your car. (If you hold the wheel steady during a turn and move at
constant speed, you are in uniform circular motion.) What you notice is a sideways acceleration because you and the car are changing direction. The
sharper the curve and the greater your speed, the more noticeable this acceleration will become. In this section we examine the direction and
magnitude of that acceleration.
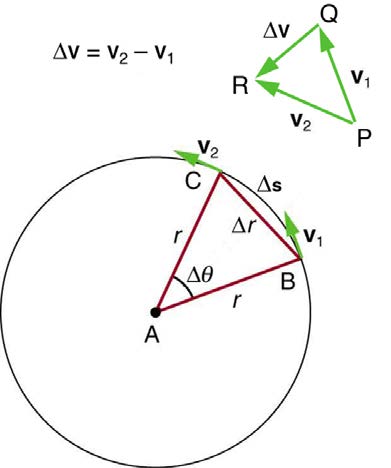
Figure 6.8 shows an object moving in a circular path at constant speed. The direction of the instantaneous velocity is shown at two points along the path. Acceleration is in the direction of the change in velocity, which points directly toward the center of rotation (the center of the circular path). This
pointing is shown with the vector diagram in the figure. We call the acceleration of an object moving in uniform circular motion (resulting from a net
external force) the centripetal acceleration( a c ); centripetal means “toward the center” or “center seeking.”
190 CHAPTER 6 | UNIFORM CIRCULAR MOTION AND GRAVITATION
Figure 6.8 The directions of the velocity of an object at two different points are shown, and the change in velocity Δv is seen to point directly toward the center of curvature.
(See small inset.) Because ac = Δv / Δ t , the acceleration is also toward the center; a c is called centripetal acceleration. (Because Δ θ is very small, the arc length Δ s is equal to the chord length Δ r for small time differences.)
The direction of centripetal acceleration is toward the center of curvature, but what is its magnitude? Note that the triangle formed by the velocity
vectors and the one formed by the radii r and Δ s are similar. Both the triangles ABC and PQR are isosceles triangles (two equal sides). The two
equal sides of the velocity vector triangle are the speeds v 1 = v 2 = v . Using the properties of two similar triangles, we obtain
(6.13)
Δ v
v = Δ s
r .
Acceleration is Δ v / Δ t , and so we first solve this expression for Δ v :
(6.14)
Δ v = vrΔ s.
Then we divide this by Δ t , yielding
(6.15)
Δ v
Δ t = vr×Δ s
Δ t.
Finally, noting that Δ v / Δ t = a c and that Δ s / Δ t = v , the linear or tangential speed, we see that the magnitude of the centripetal acceleration is (6.16)
a c = v 2 r,
which is the acceleration of an object in a circle of radius r at a speed v . So, centripetal acceleration is greater at high speeds and in sharp curves
(smaller radius), as you have noticed when driving a car. But it is a bit surprising that a c is proportional to speed squared, implying, for example, that
it is four times as hard to take a curve at 100 km/h than at 50 km/h. A sharp corner has a small radius, so that a c is greater for tighter turns, as you
have probably noticed.
It is also useful to express a c in terms of angular velocity. Substituting v = rω into the above expression, we find a c = ( rω)2 / r = rω 2 . We can express the magnitude of centripetal acceleration using either of two equations:
(6.17)
a c = v 2 r; a c = rω 2.
Recall that the direction of a c is toward the center. You may use whichever expression is more convenient, as illustrated in examples below.
A centrifuge (see Figure 6.9b) is a rotating device used to separate specimens of different densities. High centripetal acceleration significantly decreases the time it takes for separation to occur, and makes separation possible with small samples. Centrifuges are used in a variety of
applications in science and medicine, including the separation of single cell suspensions such as bacteria, viruses, and blood cells from a liquid
medium and the separation of macromolecules, such as DNA and protein, from a solution. Centrifuges are often rated in terms of their centripetal
acceleration relative to acceleration due to gravity ( g) ; maximum centripetal acceleration of several hundred thousand g is possible in a vacuum.
Human centrifuges, extremely large centrifuges, have been used to test the tolerance of astronauts to the effects of accelerations larger than that of
Earth’s gravity.

CHAPTER 6 | UNIFORM CIRCULAR MOTION AND GRAVITATION 191
Example 6.2 How Does the Centripetal Acceleration of a Car Around a Curve Compare with That Due to
Gravity?
What is the magnitude of the centripetal acceleration of a car following a curve of radius 500 m at a speed of 25.0 m/s (about 90 km/h)?
Compare the acceleration with that due to gravity for this fairly gentle curve taken at highway speed. See Figure 6.9(a).
Strategy
Because v and r are given, the first expression in a c = v 2
r ; a c = rω 2 is the most convenient to use.
Solution
Entering the given values of v = 25.0 m/s and r = 500 m into the first expression for a c gives
(6.18)
a c = v 2 r = (25.0 m/s)2
500 m = 1.25 m/s2.
Discussion
To compare this with the acceleration due to gravity ( g = 9.80 m/s2) , we take the ratio of a c / g = ⎛⎝1.25 m/s2⎞⎠ / ⎛⎝9.80 m/s2⎞⎠ = 0.128 . Thus,
a c = 0.128 g and is noticeable especially if you were not wearing a seat belt.
Figure 6.9 (a) The car following a circular path at constant speed is accelerated perpendicular to its velocity, as shown. The magnitude of this centripetal acceleration is found in Example 6.2. (b) A particle of mass in a centrifuge is rotating at constant angular velocity . It must be accelerated perpendicular to its velocity or it would continue in a straight line. The magnitude of the necessary acceleration is found in Example 6.3.
Example 6.3 How Big Is the Centripetal Acceleration in an Ultracentrifuge?
Calculate the centripetal acceleration of a point 7.50 cm from the axis of an ultracentrifuge spinning at 7.5 × 104 rev/min. Determine the
ratio of this acceleration to that due to gravity. See Figure 6.9(b).
Strategy

192 CHAPTER 6 | UNIFORM CIRCULAR MOTION AND GRAVITATION
The term rev/min stands for revolutions per minute. By converting this to radians per second, we obtain the angular velocity ω . Because r is
given, we can use the second expression in the equation a c = v 2
r ; a c = rω 2 to calculate the centripetal acceleration.
Solution
To convert 7.50×104 rev / min to radians per second, we use the facts that one revolution is 2πrad and one minute is 60.0 s. Thus,
(6.19)
ω = 7.50×104 rev
min×2π rad
1 rev × 1 min
60.0 s = 7854 rad/s.
Now the centripetal acceleration is given by the second expression in a c = v 2
r ; a c = rω 2 as
(6.20)
a c = rω 2.
Converting 7.50 cm to meters and substituting known values gives
(6.21)
a c = (0.0750 m)(7854 rad/s)2 = 4.63×106 m/s2.
Note that the unitless radians are discarded in order to get the correct units for centripetal acceleration. Taking the ratio of a c to g yields
(6.22)
a c g = 4.63×106
9.80 = 4.72×105.
Discussion
This last result means that the centripetal acceleration is 472,000 times as strong as g . It is no wonder that such high ω centrifuges are called
ultracentrifuges. The extremely large accelerations involved greatly decrease the time needed to cause the sedimentation of blood cells or other
materials.
Of course, a net external force is needed to cause any acceleration, just as Newton proposed in his second law of motion. So a net external force is
needed to cause a centripetal acceleration. In Centripetal Force, we will consider the forces involved in circular motion.
PhET Explorations: Ladybug Motion 2D
Learn about position, velocity and acceleration vectors. Move the ladybug by setting the position, velocity or acceleration, and see how the
vectors change. Choose linear, circular or elliptical motion, and record and playback the motion to analyze the behavior.
Figure 6.10 Ladybug Motion 2D (http://cnx.org/content/m42084/1.5/ladybug-motion-2d_en.jar)
6.3 Centripetal Force
Any force or combination of forces can cause a centripetal or radial acceleration. Just a few examples are the tension in the rope on a tether ball, the
force of Earth’s gravity on the Moon, friction between roller skates and a rink floor, a banked roadway’s force on a car, and forces on the tube of a
spinning centrifuge.
Any net force causing uniform circular motion is called a centripetal force. The direction of a centripetal force is toward the center of curvature, the
same as the direction of centripetal acceleration. According to Newton’s second law of motion, net force is mass times acceleration: net F = ma .
For uniform circular motion, the acceleration is the centripetal acceleration— a = ac . Thus, the magnitude of centripetal force Fc is
(6.23)
Fc = ma c.
By using the expressions for centripetal acceleration ac from ac = v 2
r ; ac = rω 2 , we get two expressions for the centripetal force Fc in terms of
mass, velocity, angular velocity, and radius of curvature:
(6.24)
Fc = mv 2 r; Fc = mrω 2.
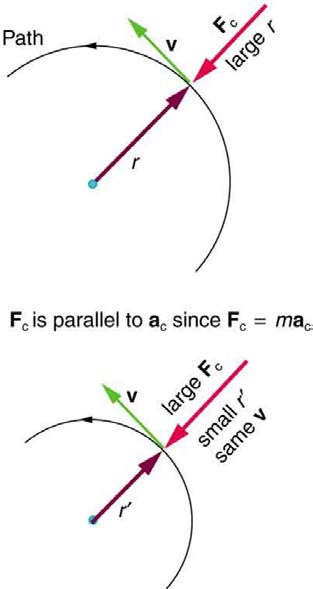
You may use whichever expression for centripetal force is more convenient. Centripetal force F c is always perpendicular to the path and pointing to
the center of curvature, because a c is perpendicular to the velocity and pointing to the center of curvature.
Note that if you solve the first expression for r , you get
CHAPTER 6 | UNIFORM CIRCULAR MOTION AND GRAVITATION 193
(6.25)
r = mv 2
F .
c
This implies that for a given mass and velocity, a large centripetal force causes a small radius of curvature—that is, a tight curve.
Figure 6.11 Centripetal force is perpendicular to velocity and causes uniform circular motion. The larger the Fc , the smaller the radius of curvature r and the sharper the curve. The second curve has the same v , but a larger Fc produces a smaller r′ .
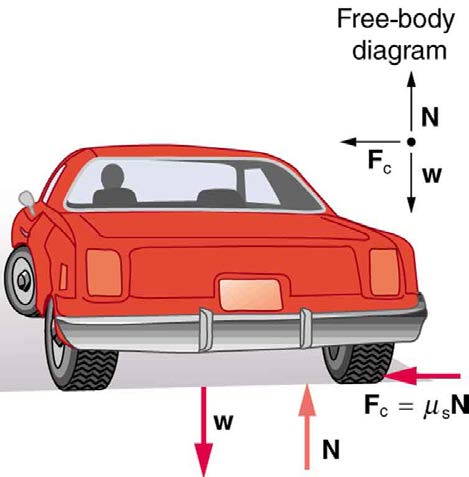
Example 6.4 What Coefficient of Friction Do Car Tires Need on a Flat Curve?
(a) Calculate the centripetal force exerted on a 900 kg car that negotiates a 500 m radius curve at 25.0 m/s.
(b) Assuming an unbanked curve, find the minimum static coefficient of friction, between the tires and the road, static friction being the reason
that keeps the car from slipping (see Figure 6.12).
Strategy and Solution for (a)
We know that F c = mv 2
r . Thus,
(6.26)
F c = mv 2
r = (900 kg)(25.0 m/s)2
(500 m)
= 1125 N.
Strategy for (b)
Figure 6.12 shows the forces acting on the car on an unbanked (level ground) curve. Friction is to the left, keeping the car from slipping, and
because it is the only horizontal force acting on the car, the friction is the centripetal force in this case. We know that the maximum static friction
(at which the tires roll but do not slip) is µ s N , where µ s is the static coefficient of friction and N is the normal force. The normal force equals
the car’s weight on level ground, so that N = mg . Thus the centripetal force in this situation is
F
(6.27)
c = f = µ s N = µ s mg.
Now we have a relationship between centripetal force and the coefficient of friction. Using the first expression for F c from the equation
(6.28)
⎫
F c = mv 2 r ⎬ ,
F
⎭
c = mrω 2
(6.29)
mv 2 r = µ s mg.
We solve this for µ s , noting that mass cancels, and obtain
194 CHAPTER 6 | UNIFORM CIRCULAR MOTION AND GRAVITATION
(6.30)
µ s = v 2
rg.
Solution for (b)
Substituting the knowns,
(6.31)
µ s =
(25.0 m/s)2
= 0.13.
(500 m)(9.80 m/s2)
(Because coefficients of friction are approximate, the answer is given to only two digits.)
Discussion
⎫
We could also solve part (a) using the first expression in F c = mv 2
r ⎬ , because m, v, and r are given. The coefficient of friction found in
F
⎭
c = mrω 2
part (b) is much smaller than is typically found between tires and roads. The car will still negotiate the curve if the coefficient is greater than 0.13,
because static friction is a responsive force, being able to assume a value less than but no more than µ s N . A higher coefficient would also
allow the car to negotiate the curve at a higher spee











