Example 8.2 Calculating Force: Venus Williams’ Racquet
During the 2007 French Open, Venus Williams hit the fastest recorded serve in a premier women’s match, reaching a speed of 58 m/s (209 km/
h). What is the average force exerted on the 0.057-kg tennis ball by Venus Williams’ racquet, assuming that the ball’s speed just after impact is
58 m/s, that the initial horizontal component of the velocity before impact is negligible, and that the ball remained in contact with the racquet for
5.0 ms (milliseconds)?
Strategy
This problem involves only one dimension because the ball starts from having no horizontal velocity component before impact. Newton’s second
law stated in terms of momentum is then written as
(8.13)
Fnet = Δp
Δ t .
As noted above, when mass is constant, the change in momentum is given by
(8.14)
Δ p = mΔ v = m( v f − v i).
In this example, the velocity just after impact and the change in time are given; thus, once Δ p is calculated, F net = Δ p
Δ t can be used to find
the force.
Solution
To determine the change in momentum, substitute the values for the initial and final velocities into the equation above.
(8.15)
Δ p = m( v f – v i)
= ⎛⎝0.057 kg⎞⎠(58 m/s – 0 m/s)
= 3.306 kg · m/s ≈ 3.3 kg · m/s
Now the magnitude of the net external force can determined by using F net = Δ p
Δ t :
(8.16)
F net = Δ p
Δ t = 3.306 kg ⋅ m/s
5.0×10−3 s
= 661 N ≈ 660 N,
264 CHAPTER 8 | LINEAR MOMENTUM AND COLLISIONS
where we have retained only two significant figures in the final step.
Discussion
This quantity was the average force exerted by Venus Williams’ racquet on the tennis ball during its brief impact (note that the ball also
experienced the 0.56-N force of gravity, but that force was not due to the racquet). This problem could also be solved by first finding the
acceleration and then using F net = ma , but one additional step would be required compared with the strategy used in this example.
8.2 Impulse
The effect of a force on an object depends on how long it acts, as well as how great the force is. In Example 8.1, a very large force acting for a short time had a great effect on the momentum of the tennis ball. A small force could cause the same change in momentum, but it would have to act for a
much longer time. For example, if the ball were thrown upward, the gravitational force (which is much smaller than the tennis racquet’s force) would
eventually reverse the momentum of the ball. Quantitatively, the effect we are talking about is the change in momentum Δp .
By rearranging the equation Fnet = Δp
Δ t to be
(8.17)
Δp = FnetΔ t,
we can see how the change in momentum equals the average net external force multiplied by the time this force acts. The quantity Fnet Δ t is given
the name impulse. Impulse is the same as the change in momentum.
Impulse: Change in Momentum
Change in momentum equals the average net external force multiplied by the time this force acts.
(8.18)
Δp = FnetΔ t
The quantity Fnet Δ t is given the name impulse.
There are many ways in which an understanding of impulse can save lives, or at least limbs. The dashboard padding in a car, and certainly the
airbags, allow the net force on the occupants in the car to act over a much longer time when there is a sudden stop. The momentum change is
the same for an occupant, whether an air bag is deployed or not, but the force (to bring the occupant to a stop) will be much less if it acts over a
larger time. Cars today have many plastic components. One advantage of plastics is their lighter weight, which results in better gas mileage.
Another advantage is that a car will crumple in a collision, especially in the event of a head-on collision. A longer collision time means the force
on the car will be less. Deaths during car races decreased dramatically when the rigid frames of racing cars were replaced with parts that could
crumple or collapse in the event of an accident.
Bones in a body will fracture if the force on them is too large. If you jump onto the floor from a table, the force on your legs can be immense if you
land stiff-legged on a hard surface. Rolling on the ground after jumping from the table, or landing with a parachute, extends the time over which
the force (on you from the ground) acts.
Example 8.3 Calculating Magnitudes of Impulses: Two Billiard Balls Striking a Rigid Wall
Two identical billiard balls strike a rigid wall with the same speed, and are reflected without any change of speed. The first ball strikes
perpendicular to the wall. The second ball strikes the wall at an angle of 30º from the perpendicular, and bounces off at an angle of 30º from
perpendicular to the wall.
(a) Determine the direction of the force on the wall due to each ball.
(b) Calculate the ratio of the magnitudes of impulses on the two balls by the wall.
Strategy for (a)
In order to determine the force on the wall, consider the force on the ball due to the wall using Newton’s second law and then apply Newton’s
third law to determine the direction. Assume the x -axis to be normal to the wall and to be positive in the initial direction of motion. Choose the y
-axis to be along the wall in the plane of the second ball’s motion. The momentum direction and the velocity direction are the same.
Solution for (a)
The first ball bounces directly into the wall and exerts a force on it in the +x direction. Therefore the wall exerts a force on the ball in the −x
direction. The second ball continues with the same momentum component in the y direction, but reverses its x -component of momentum, as
seen by sketching a diagram of the angles involved and keeping in mind the proportionality between velocity and momentum.
These changes mean the change in momentum for both balls is in the −x direction, so the force of the wall on each ball is along the −x
direction.
Strategy for (b)
Calculate the change in momentum for each ball, which is equal to the impulse imparted to the ball.
Solution for (b)
CHAPTER 8 | LINEAR MOMENTUM AND COLLISIONS 265
Let u be the speed of each ball before and after collision with the wall, and m the mass of each ball. Choose the x -axis and y -axis as
previously described, and consider the change in momentum of the first ball which strikes perpendicular to the wall.
p
(8.19)
xi = mu; p yi = 0
p
(8.20)
xf = − mu; p yf = 0
Impulse is the change in momentum vector. Therefore the x -component of impulse is equal to −2 mu and the y -component of impulse is
equal to zero.
Now consider the change in momentum of the second ball.
p
(8.21)
xi = mu cos 30º; p yi = –mu sin 30º
p
(8.22)
xf = – mu cos 30º; p yf = − mu sin 30º
It should be noted here that while p x changes sign after the collision, p y does not. Therefore the x -component of impulse is equal to
−2 mu cos 30º and the y -component of impulse is equal to zero.
The ratio of the magnitudes of the impulse imparted to the balls is
(8.23)
2 mu
2 mu cos 30º = 2 = 1.155.
3
Discussion
The direction of impulse and force is the same as in the case of (a); it is normal to the wall and along the negative x - direction. Making use of
Newton’s third law, the force on the wall due to each ball is normal to the wall along the positive x -direction.
Our definition of impulse includes an assumption that the force is constant over the time interval Δ t . Forces are usually not constant. Forces vary
considerably even during the brief time intervals considered. It is, however, possible to find an average effective force F eff that produces the same
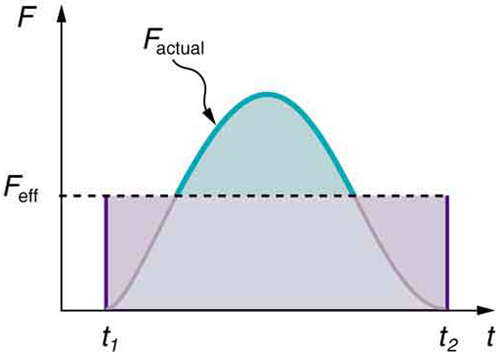
result as the corresponding time-varying force. Figure 8.2 shows a graph of what an actual force looks like as a function of time for a ball bouncing off the floor. The area under the curve has units of momentum and is equal to the impulse or change in momentum between times t 1 and t 2 . That
area is equal to the area inside the rectangle bounded by F eff , t 1 , and t 2 . Thus the impulses and their effects are the same for both the actual
and effective forces.
Figure 8.2 A graph of force versus time with time along the x -axis and force along the y -axis for an actual force and an equivalent effective force. The areas under the two curves are equal.
Making Connections: Take-Home Investigation—Hand Movement and Impulse
Try catching a ball while “giving” with the ball, pulling your hands toward your body. Then, try catching a ball while keeping your hands still. Hit
water in a tub with your full palm. After the water has settled, hit the water again by diving your hand with your fingers first into the water. (Your
full palm represents a swimmer doing a belly flop and your diving hand represents a swimmer doing a dive.) Explain what happens in each case
and why. Which orientations would you advise people to avoid and why?
Making Connections: Constant Force and Constant Acceleration
The assumption of a constant force in the definition of impulse is analogous to the assumption of a constant acceleration in kinematics. In both
cases, nature is adequately described without the use of calculus.
266 CHAPTER 8 | LINEAR MOMENTUM AND COLLISIONS
8.3 Conservation of Momentum
Momentum is an important quantity because it is conserved. Yet it was not conserved in the examples in Impulse and Linear Momentum and
Force, where large changes in momentum were produced by forces acting on the system of interest. Under what circumstances is momentum
conserved?
The answer to this question entails considering a sufficiently large system. It is always possible to find a larger system in which total momentum is
constant, even if momentum changes for components of the system. If a football player runs into the goalpost in the end zone, there will be a force on
him that causes him to bounce backward. However, the Earth also recoils —conserving momentum—because of the force applied to it through the
goalpost. Because Earth is many orders of magnitude more massive than the player, its recoil is immeasurably small and can be neglected in any
practical sense, but it is real nevertheless.
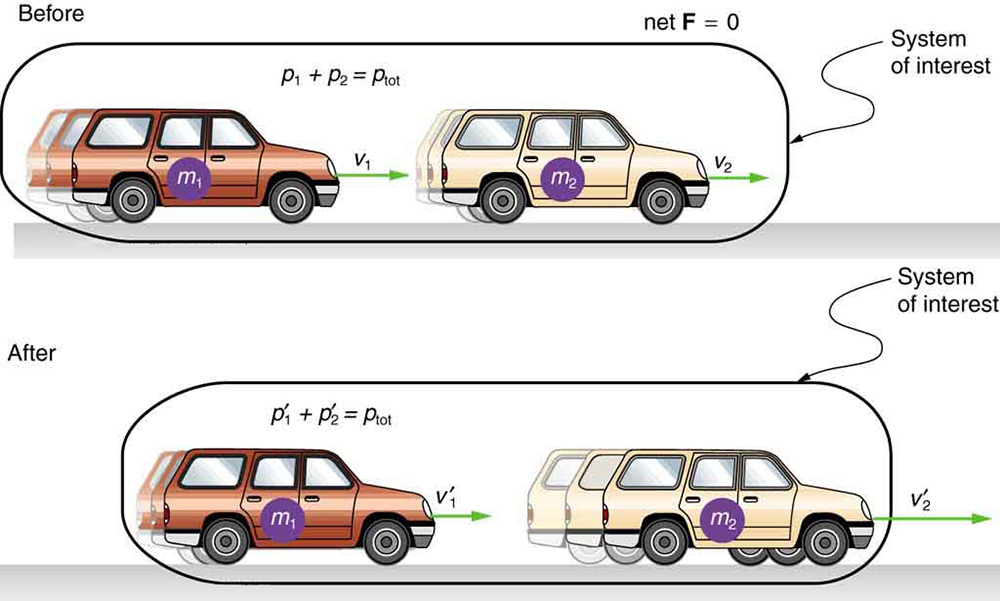
Consider what happens if the masses of two colliding objects are more similar than the masses of a football player and Earth—for example, one car
bumping into another, as shown in Figure 8.3. Both cars are coasting in the same direction when the lead car (labeled m 2) is bumped by the trailing car (labeled m 1). The only unbalanced force on each car is the force of the collision. (Assume that the effects due to friction are negligible.) Car 1
slows down as a result of the collision, losing some momentum, while car 2 speeds up and gains some momentum. We shall now show that the total
momentum of the two-car system remains constant.
Figure 8.3 A car of mass m 1 moving with a velocity of v 1 bumps into another car of mass m 2 and velocity v 2 that it is following. As a result, the first car slows down to a velocity of v′1 and the second speeds up to a velocity of v′2 . The momentum of each car is changed, but the total momentum p tot of the two cars is the same before
and after the collision (if you assume friction is negligible).
Using the definition of impulse, the change in momentum of car 1 is given by
(8.24)
Δ p 1 = F 1Δ t,
where F 1 is the force on car 1 due to car 2, and Δ t is the time the force acts (the duration of the collision). Intuitively, it seems obvious that the
collision time is the same for both cars, but it is only true for objects traveling at ordinary speeds. This assumption must be modified for objects
travelling near the speed of light, without affecting the result that momentum is conserved.
Similarly, the change in momentum of car 2 is
(8.25)
Δ p 2 = F 2Δ t,
where F 2 is the force on car 2 due to car 1, and we assume the duration of the collision Δ t is the same for both cars. We know from Newton’s third
law that F 2 = – F 1 , and so
(8.26)
Δ p 2 = − F 1Δ t = −Δ p 1.
Thus, the changes in momentum are equal and opposite, and
(8.27)
Δ p 1 + Δ p 2 = 0.
Because the changes in momentum add to zero, the total momentum of the two-car system is constant. That is,
p
(8.28)
1 + p 2 = constant,
p
(8.29)
1 + p 2 = p′1 + p′2,

CHAPTER 8 | LINEAR MOMENTUM AND COLLISIONS 267
where p′1 and p′2 are the momenta of cars 1 and 2 after the collision. (We often use primes to denote the final state.)
This result—that momentum is conserved—has validity far beyond the preceding one-dimensional case. It can be similarly shown that total
momentum is conserved for any isolated system, with any number of objects in it. In equation form, the conservation of momentum principle for an
isolated system is written
p
(8.30)
tot = constant,
or
(8.31)
ptot = p′tot,
where ptot is the total momentum (the sum of the momenta of the individual objects in the system) and p′tot is the total momentum some time
later. (The total momentum can be shown to be the momentum of the center of mass of the system.) An isolated system is defined to be one for
which the net external force is zero ⎛⎝Fnet = 0⎞⎠.
Conservation of Momentum Principle
p
(8.32)
tot = constant
ptot = p′tot (isolated system)
Isolated System
An isolated system is defined to be one for which the net external force is zero ⎛⎝Fnet = 0⎞⎠.
Perhaps an easier way to see that momentum is conserved for an isolated system is to consider Newton’s second law in terms of momentum,
Fnet = Δptot
Δ t . For an isolated system, ⎛⎝Fnet = 0⎞⎠ ; thus, Δptot = 0 , and ptot is constant.
We have noted that the three length dimensions in nature— x , y , and z —are independent, and it is interesting to note that momentum can be
conserved in different ways along each dimension. For example, during projectile motion and where air resistance is negligible, momentum is
conserved in the horizontal direction because horizontal forces are zero and momentum is unchanged. But along the vertical direction, the net vertical
force is not zero and the momentum of the projectile is not conserved. (See Figure 8.4.) However, if the momentum of the projectile-Earth system is considered in the vertical direction, we find that the total momentum is conserved.
Figure 8.4 The horizontal component of a projectile’s momentum is conserved if air resistance is negligible, even in this case where a space probe separates. The forces
causing the separation are internal to the system, so that the net external horizontal force Fx – net is still zero. The vertical component of the momentum is not conserved,
because the net vertical force Fy – net is not zero. In the vertical direction, the space probe-Earth system needs to be considered and we find that the total momentum is
conserved. The center of mass of the space probe takes the same path it would if the separation did not occur.
The conservation of momentum principle can be applied to systems as different as a comet striking Earth and a gas containing huge numbers of
atoms and molecules. Conservation of momentum is violated only when the net external force is not zero. But another larger system can always be
considered in which momentum is conserved by simply including the source of the external force. For example, in the collision of two cars considered
above, the two-car system conserves momentum while each one-car system does not.
268 CHAPTER 8 | LINEAR MOMENTUM AND COLLISIONS
Making Connections: Take-Home Investigation—Drop of Tennis Ball and a Basketball
Hold a tennis ball side by side and in contact with a basketball. Drop the balls together. (Be careful!) What happens? Explain your observations.
Now hold the tennis ball above and in contact with the basketball. What happened? Explain your observations. What do you think will happen if
the basketball ball is held above and in contact with the tennis ball?
Making Connections: Take-Home Investigation—Two Tennis Balls in a Ballistic Trajectory
Tie two tennis balls together with a string about a foot long. Hold one ball and let the other hang down and throw it in a ballistic trajectory. Explain
your observations. Now mark the center of the string with bright ink or attach a brightly colored sticker to it and throw again. What happened?
Explain your observations.
Some aquatic animals such as jellyfish move around based on the principles of conservation of momentum. A jellyfish fills its umbrella section
with water and then pushes the water out resulting in motion in the opposite direction to that of the jet of water. Squids propel themselves in a
similar manner but, in contrast with jellyfish, are able to control the direction in which they move by aiming their nozzle forward or backward.
Typical squids can move at speeds of 8 to 12 km/h.
The ballistocardiograph (BCG) was a diagnostic tool used in the second half of the 20th century to study the strength of the heart. About once a
second, your heart beats, forcing blood into the aorta. A force in the opposite direction is exerted on the rest of your body (recall Newton’s third
law). A ballistocardiograph is a device that can measure this reaction force. This measurement is done by using a sensor (resting on the person)
or by using a moving table suspended from the ceiling. This technique can gather information on the strength of the heart beat and the volume of
blood passing from the heart. However, the electrocardiogram (ECG or EKG) and the echocardiogram (cardiac ECHO or ECHO; a technique that
uses ultrasound to see an image of the heart) are more widely used in the practice of cardiology.
Making Connections: Conservation of Momentum and Collision
Conservation of momentum is quite useful in describing collisions. Momentum is crucial to our understanding of atomic and subatomic particles
because much of what we know about these particles comes from collision experiments.
Subatomic Collisions and Momentum
The conservation of momentum principle not only applies to the macroscopic objects, it is also essential to our explorations of atomic and subatomic
particles. Giant machines hurl subatomic particles at one another, and researchers evaluate the results by assuming conservation of momentum
(among other things).
On the small scale, we find that particles and their properties are invisible to the naked eye but can be measured with our instruments, and models of
these subatomic particles can be constructed to describe the results. Momentum is found to be a property of all subatomic particles including
massless particles such as photons that compose light. Momentum being a property of particles hints that momentum may have an identity beyond
the description of an object’s mass multiplied by the object’s velocity. Indeed, momentum relates to wave properties and plays a fundamental role in
what measurements are taken and how we take these measurements. Furthermore, we find that the conservation of momentum principle is valid
when considering systems of particles. We use this principle to analyze the masses and other properties of previously undetected particles, such as
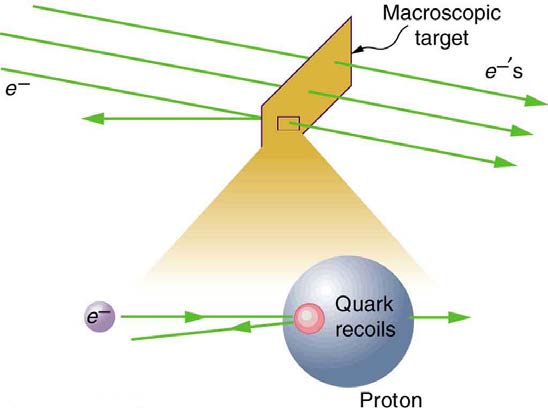
the nucleus of an atom and the existence of quarks that make up particles of nuclei. Figure 8.5 below illustrates how a particle scattering backward from another implies that its target is massive and dense. Experiments seeking evidence that quarks make up protons (one type of particle that
makes up nuclei) scattered high-energy electrons off of protons (nuclei of hydrogen atoms). Electrons occasionally scattered straight backward in a
manner that implied a very small and very dense particle makes up the proton—this observation is considered nearly direct evidence of quarks. The
analysis was based partly on the same conservation of momentum principle that works so well on the large scale.
Figure 8.5 A subatomic particle scatters straight backward from a target particle. In experiments seeking evidence for quarks, electrons were observed to occasionally scatter
straight backward from a proton.
CHAPTER 8 | LINEAR MOMENTUM AND COLLISIONS 269
8.4 Elastic Collisions in One Dimension
Let us consider various types of two-object collisions. These collisions are the easiest to analyze, and they illustrate many of the physical principles
involved in collisions. The conservation of momentum principle is very useful here, and it can be used whenever the net external force on a system is
zero.
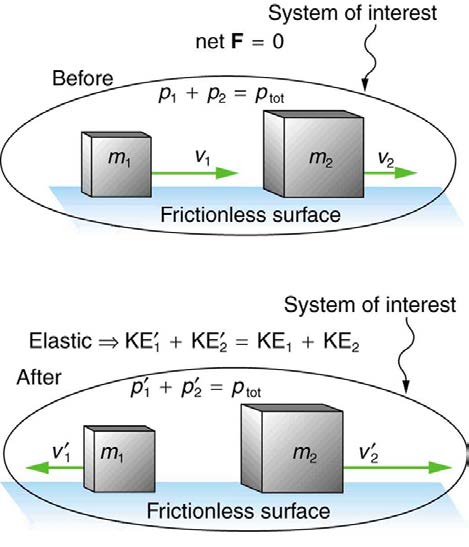
We start with the elastic collision of two objects moving along the same line—a one-dimensional problem. An elastic collision is one that also
conserves internal kinetic energy. Internal kinetic energy is the sum of the kinetic energies of the objects in the system. Figure 8.6 illustrates an elastic collision in which internal kinetic energy and momentum are conserved.
Truly elastic collisions can only be achieved with subatomic particles, such as electrons striking nuclei. Macroscopic collisions can be very nearly, but
not quite, elastic—some kinetic energy is always converted into other forms of energy such as heat transfer due to friction and sound. One
macroscopic collision that is nearly elastic is that of two steel blocks on ice. Another nearly elastic collision is that between two carts with spring
bumpers on an air track. Icy surfaces and air tracks are nearly frictionless, more readily allowing nearly elastic collisions on them.
Elastic Collision
An elastic collision is one that conserves internal kinetic energy.
Internal Kinetic Energy
Internal kinetic energy is the sum of t








