1. Find a racquet (a tennis, badminton, or other racquet will do). Place the racquet on the floor and stand on the handle. Drop a tennis ball on
the strings from a measured height. Measure how high the ball bounces. Now ask a friend to hold the racquet firmly by the handle and drop
a tennis ball from the same measured height above the racquet. Measure how high the ball bounces and observe what happens to your
friend’s hand during the collision. Explain your observations and measurements.
2. The coefficient of restitution ( c) is a measure of the elasticity of a collision between a ball and an object, and is defined as the ratio of the
speeds after and before the collision. A perfectly elastic collision has a c of 1. For a ball bouncing off the floor (or a racquet on the floor),
c can be shown to be c = ( h / H)1/2 where h is the height to which the ball bounces and H is the height from which the ball is
dropped. Determine c for the cases in Part 1 and for the case of a tennis ball bouncing off a concrete or wooden floor ( c = 0.85 for new
tennis balls used on a tennis court).
Example 8.6 Calculating Final Velocity and Energy Release: Two Carts Collide
In the collision pictured in Figure 8.10, two carts collide inelastically. Cart 1 (denoted m 1 carries a spring which is initially compressed. During the collision, the spring releases its potential energy and converts it to internal kinetic energy. The mass of cart 1 and the spring is 0.350 kg, and
the cart and the spring together have an initial velocity of 2.00 m/s . Cart 2 (denoted m 2 in Figure 8.10) has a mass of 0.500 kg and an initial velocity of −0.500 m/s . After the collision, cart 1 is observed to recoil with a velocity of −4.00 m/s . (a) What is the final velocity of cart 2? (b)
How much energy was released by the spring (assuming all of it was converted into internal kinetic energy)?
Strategy
274 CHAPTER 8 | LINEAR MOMENTUM AND COLLISIONS
We can use conservation of momentum to find the final velocity of cart 2, because F net = 0 (the track is frictionless and the force of the spring
is internal). Once this velocity is determined, we can compare the internal kinetic energy before and after the collision to see how much energy
was released by the spring.
Solution for (a)
As before, the equation for conservation of momentum in a two-object system is
m
(8.53)
1 v 1 + m 2 v 2 = m 1 v′1 + m 2 v′2 .
The only unknown in this equation is v′1 . Solving for v′2 and substituting known values into the previous equation yields
(8.54)
v′2 = m 1 v 1 + m 2 v 2 − m 1 v′1
m 2
⎛
⎛
= ⎝0.350 kg⎞⎠(2.00 m/s) + ⎛⎝0.500 kg⎞⎠(−0.500 m/s) ⎝0.350 kg⎞⎠(−4.00 m/s)
0.500 kg
−
0.500 kg
= 3.70 m/s.
Solution for (b)
The internal kinetic energy before the collision is
2
2
(8.55)
KEint = 12 m 1 v 1 + 12 m 2 v 2
= 1⎛
⎛
2⎝0.350 kg⎞⎠(2.00 m/s)2 + 12⎝0.500 kg⎞⎠( – 0.500 m/s)2
= 0.763 J.
After the collision, the internal kinetic energy is
2
2
(8.56)
KE′int = 12 m 1 v′1 + 12 m 2 v′2
= 1⎛
⎛
2⎝0.350 kg⎞⎠(-4.00 m/s)2 + 12⎝0.500 kg⎞⎠(3.70 m/s)2
= 6.22 J.
The change in internal kinetic energy is thus
(8.57)
KE′int − KEint = 6.22 J − 0.763 J
= 5.46 J.
Discussion
The final velocity of cart 2 is large and positive, meaning that it is moving to the right after the collision. The internal kinetic energy in this collision
increases by 5.46 J. That energy was released by the spring.
8.6 Collisions of Point Masses in Two Dimensions
In the previous two sections, we considered only one-dimensional collisions; during such collisions, the incoming and outgoing velocities are all along
the same line. But what about collisions, such as those between billiard balls, in which objects scatter to the side? These are two-dimensional
collisions, and we shall see that their study is an extension of the one-dimensional analysis already presented. The approach taken (similar to the
approach in discussing two-dimensional kinematics and dynamics) is to choose a convenient coordinate system and resolve the motion into
components along perpendicular axes. Resolving the motion yields a pair of one-dimensional problems to be solved simultaneously.
One complication arising in two-dimensional collisions is that the objects might rotate before or after their collision. For example, if two ice skaters
hook arms as they pass by one another, they will spin in circles. We will not consider such rotation until later, and so for now we arrange things so
that no rotation is possible. To avoid rotation, we consider only the scattering of point masses—that is, structureless particles that cannot rotate or
spin.
We start by assuming that Fnet = 0 , so that momentum p is conserved. The simplest collision is one in which one of the particles is initially at rest.
(See Figure 8.11.) The best choice for a coordinate system is one with an axis parallel to the velocity of the incoming particle, as shown in Figure
8.11. Because momentum is conserved, the components of momentum along the x - and y -axes ( px and py) will also be conserved, but with the chosen coordinate system, py is initially zero and px is the momentum of the incoming particle. Both facts simplify the analysis. (Even with the
simplifying assumptions of point masses, one particle initially at rest, and a convenient coordinate system, we still gain new insights into nature from
the analysis of two-dimensional collisions.)

CHAPTER 8 | LINEAR MOMENTUM AND COLLISIONS 275
Figure 8.11 A two-dimensional collision with the coordinate system chosen so that m 2 is initially at rest and v 1 is parallel to the x -axis. This coordinate system is sometimes called the laboratory coordinate system, because many scattering experiments have a target that is stationary in the laboratory, while particles are scattered from it
to determine the particles that make-up the target and how they are bound together. The particles may not be observed directly, but their initial and final velocities are.
Along the x -axis, the equation for conservation of momentum is
p
(8.58)
1 x + p 2 x = p′1 x + p′2 x.
Where the subscripts denote the particles and axes and the primes denote the situation after the collision. In terms of masses and velocities, this
equation is
m
(8.59)
1 v 1 x + m 2 v 2 x = m 1 v′1 x + m 2 v′2 x.
But because particle 2 is initially at rest, this equation becomes
m
(8.60)
1 v 1 x = m 1 v′1 x + m 2 v′2 x.
The components of the velocities along the x -axis have the form v cos θ . Because particle 1 initially moves along the x -axis, we find v 1 x = v 1 .
Conservation of momentum along the x -axis gives the following equation:
m
(8.61)
1 v 1 = m 1 v′1 cos θ 1 + m 2 v′2 cos θ 2,
where θ 1 and θ 2 are as shown in Figure 8.11.
Conservation of Momentum along the x -axis
m
(8.62)
1 v 1 = m 1 v′1 cos θ 1 + m 2 v′2 cos θ 2
Along the y -axis, the equation for conservation of momentum is
p
(8.63)
1 y + p 2 y = p′1 y + p′2 y
or
m
(8.64)
1 v 1 y + m 2 v 2 y = m 1 v′1 y + m 2 v′2 y.
But v 1 y is zero, because particle 1 initially moves along the x -axis. Because particle 2 is initially at rest, v 2 y is also zero. The equation for conservation of momentum along the y -axis becomes
(8.65)
0 = m 1 v′1 y + m 2 v′2 y.
The components of the velocities along the y -axis have the form v sin θ .
Thus, conservation of momentum along the y -axis gives the following equation:
(8.66)
0 = m 1 v′1 sin θ 1 + m 2 v′2 sin θ 2.
Conservation of Momentum along the y -axis
(8.67)
0 = m 1 v′1 sin θ 1 + m 2 v′2 sin θ 2
276 CHAPTER 8 | LINEAR MOMENTUM AND COLLISIONS
The equations of conservation of momentum along the x -axis and y -axis are very useful in analyzing two-dimensional collisions of particles, where
one is originally stationary (a common laboratory situation). But two equations can only be used to find two unknowns, and so other data may be
necessary when collision experiments are used to explore nature at the subatomic level.
Example 8.7 Determining the Final Velocity of an Unseen Object from the Scattering of Another Object
Suppose the following experiment is performed. A 0.250-kg object ( m 1) is slid on a frictionless surface into a dark room, where it strikes an
initially stationary object with mass of 0.400 kg ( m 2) . The 0.250-kg object emerges from the room at an angle of 45.0º with its incoming
direction.
The speed of the 0.250-kg object is originally 2.00 m/s and is 1.50 m/s after the collision. Calculate the magnitude and direction of the velocity
( v′2 and θ 2) of the 0.400-kg object after the collision.
Strategy
Momentum is conserved because the surface is frictionless. The coordinate system shown in Figure 8.12 is one in which m 2 is originally at rest and the initial velocity is parallel to the x -axis, so that conservation of momentum along the x - and y -axes is applicable.
Everything is known in these equations except v′2 and θ 2 , which are precisely the quantities we wish to find. We can find two unknowns
because we have two independent equations: the equations describing the conservation of momentum in the x - and y -directions.
Solution
Solving m 1 v 1 = m 1 v′1 cos θ 1 + m 2 v′2 cos θ 2 and 0 = m 1 v′1 sin θ 1 + m 2 v′2 sin θ 2 for v′2 sin θ 2 and taking the ratio yields an
⎛
⎞
equation (because ⎝tan θ = sin θ
cos θ⎠ in which all but one quantity is known:
(8.68)
tan θ 2 = v′1 sin θ 1
v′
.
1 cos θ 1 − v 1
Entering known values into the previous equation gives
(8.69)
tan θ 2 =
(1.50 m/s)(0.7071)
(1.50 m/s)(0.7071) − 2.00 m/s = −1.129.
Thus,
(8.70)
θ 2 = tan−1(−1.129) = 311.5º ≈ 312º.
Angles are defined as positive in the counter clockwise direction, so this angle indicates that m 2 is scattered to the right in Figure 8.12, as expected (this angle is in the fourth quadrant). Either equation for the x - or y -axis can now be used to solve for v′2 , but the latter equation is
easiest because it has fewer terms.
(8.71)
v′
sin θ 1
2 = − m 1
m v′
2 1 sin θ 2
Entering known values into this equation gives
(8.72)
v′
0.250 kg⎞
0.7071 ⎞
2 = −⎛⎝0.400 kg⎠(1.50 m/s)⎛⎝−0.7485⎠.
Thus,
v
(8.73)
′2 = 0.886 m/s.
Discussion
It is instructive to calculate the internal kinetic energy of this two-object system before and after the collision. (This calculation is left as an end-of-
chapter problem.) If you do this calculation, you will find that the internal kinetic energy is less after the collision, and so the collision is inelastic.
This type of result makes a physicist want to explore the system further.
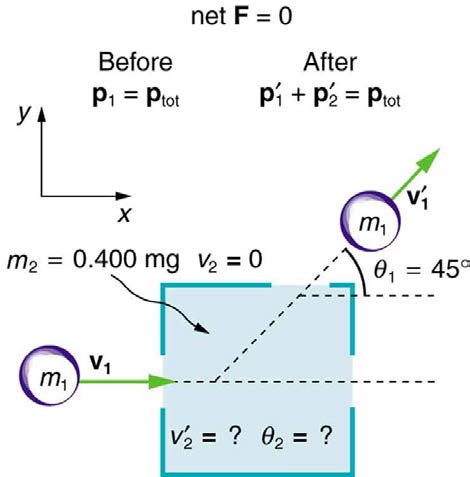
CHAPTER 8 | LINEAR MOMENTUM AND COLLISIONS 277
Figure 8.12 A collision taking place in a dark room is explored in Example 8.7. The incoming object m 1 is scattered by an initially stationary object. Only the stationary object’s mass m 2 is known. By measuring the angle and speed at which m 1 emerges from the room, it is possible to calculate the magnitude and direction of the initially stationary object’s velocity after the collision.
Elastic Collisions of Two Objects with Equal Mass
Some interesting situations arise when the two colliding objects have equal mass and the collision is elastic. This situation is nearly the case with
colliding billiard balls, and precisely the case with some subatomic particle collisions. We can thus get a mental image of a collision of subatomic
particles by thinking about billiards (or pool). (Refer to Figure 8.11 for masses and angles.) First, an elastic collision conserves internal kinetic energy.
Again, let us assume object 2 ( m 2) is initially at rest. Then, the internal kinetic energy before and after the collision of two objects that have equal
masses is
2
2
2
(8.74)
12 mv 1 = 12 mv′1 + 12 mv′2 .
Because the masses are equal, m 1 = m 2 = m . Algebraic manipulation (left to the reader) of conservation of momentum in the x - and y -
directions can show that
2
2
2
⎞
(8.75)
12 mv 1 = 12 mv′1 + 12 mv′2 + mv′1 v′2 cos⎛⎝ θ 1− θ 2⎠.
(Remember that θ 2 is negative here.) The two preceding equations can both be true only if
⎞
(8.76)
mv′1 v′2 cos⎛⎝ θ 1 − θ 2⎠ = 0.
There are three ways that this term can be zero. They are
•
v′1 = 0 : head-on collision; incoming ball stops
•
v′2 = 0 : no collision; incoming ball continues unaffected
•
cos( θ 1 − θ 2) = 0 : angle of separation ( θ 1 − θ 2) is 90º after the collision
All three of these ways are familiar occurrences in billiards and pool, although most of us try to avoid the second. If you play enough pool, you will
notice that the angle between the balls is very close to 90º after the collision, although it will vary from this value if a great deal of spin is placed on
the ball. (Large spin carries in extra energy and a quantity called angular momentum, which must also be conserved.) The assumption that the
scattering of billiard balls is elastic is reasonable based on the correctness of the three results it produces. This assumption also implies that, to a
good approximation, momentum is conserved for the two-ball system in billiards and pool. The problems below explore these and other
characteristics of two-dimensional collisions.
Connections to Nuclear and Particle Physics
Two-dimensional collision experiments have revealed much of what we know about subatomic particles, as we shall see in Medical
Applications of Nuclear Physics and Particle Physics. Ernest Rutherford, for example, discovered the nature of the atomic nucleus from such
experiments.
8.7 Introduction to Rocket Propulsion
Rockets range in size from fireworks so small that ordinary people use them to immense Saturn Vs that once propelled massive payloads toward the
Moon. The propulsion of all rockets, jet engines, deflating balloons, and even squids and octopuses is explained by the same physical
278 CHAPTER 8 | LINEAR MOMENTUM AND COLLISIONS
principle—Newton’s third law of motion. Matter is forcefully ejected from a system, producing an equal and opposite reaction on what remains.
Another common example is the recoil of a gun. The gun exerts a force on a bullet to accelerate it and consequently experiences an equal and
opposite force, causing the gun’s recoil or kick.
Making Connections: Take-Home Experiment—Propulsion of a Balloon
Hold a balloon and fill it with air. Then, let the balloon go. In which direction does the air come out of the balloon and in which direction does the
balloon get propelled? If you fill the balloon with water and then let the balloon go, does the balloon’s direction change? Explain your answer.
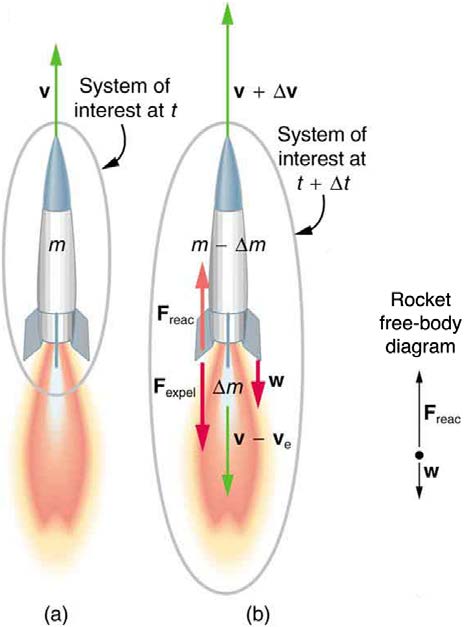
Figure 8.13 shows a rocket accelerating straight up. In part (a), the rocket has a mass m and a velocity v relative to Earth, and hence a momentum mv . In part (b), a time Δ t has elapsed in which the rocket has ejected a mass Δ m of hot gas at a velocity v e relative to the rocket. The
remainder of the mass ( m − Δ m) now has a greater velocity ( v + Δ v) . The momentum of the entire system (rocket plus expelled gas) has
actually decreased because the force of gravity has acted for a time Δ t , producing a negative impulse Δ p = − mgΔ t . (Remember that impulse is
the net external force on a system multiplied by the time it acts, and it equals the change in momentum of the system.) So, the center of mass of the
system is in free fall but, by rapidly expelling mass, part of the system can accelerate upward. It is a commonly held misconception that the rocket
exhaust pushes on the ground. If we consider thrust; that is, the force exerted on the rocket by the exhaust gases, then a rocket’s thrust is greater in
outer space than in the atmosphere or on the launch pad. In fact, gases are easier to expel into a vacuum.
By calculating the change in momentum for the entire system over Δ t , and equating this change to the impulse, the following expression can be
shown to be a good approximation for the acceleration of the rocket.
(8.77)
a = v e Δ m
m Δ t − g
“The rocket” is that part of the system remaining after the gas is ejected, and g is the acceleration due to gravity.
Acceleration of a Rocket
Acceleration of a rocket is
(8.78)
a = v e Δ m
m Δ t − g,
where a is the acceleration of the rocket, v e is the escape velocity, m is the mass of the rocket, Δ m is the mass of the ejected gas, and Δ t
is the time in which the gas is ejected.
Figure 8.13 (a) This rocket has a mass m and an upward velocity v . The net external force on the system is − mg , if air resistance is neglected. (b) A time Δ t later the system has two main parts, the ejected gas and the remainder of the rocket. The reaction force on the rocket is what overcomes the gravitational force and accelerates it
upward.
CHAPTER 8 | LINEAR MOMENTUM AND COLLISIONS 279
A rocket’s acceleration depends on three major factors, consistent with the equation for acceleration of a rocket . First, the greater the exhaust
velocity of the gases relative to the rocket, v e , the greater the acceleration is. The practical limit for v e is about 2.5×103 m/s for conventional
(non-nuclear) hot-gas propulsion systems. The second factor is the rate at which mass is ejected from the rocket. This is the factor Δ m / Δ t in the
equation. The quantity (Δ m / Δ t) v e , with units of newtons, is called "thrust.” The faster the rocket burns its fuel, the greater its thrust, and the
greater its acceleration. The third factor is the mass m of the rocket. The smaller the mass is (all other factors being the same), the greater the
acceleration. The rocket mass m decreases dramatically during flight because most of the rocket is fuel to begin with, so that acceleration increases
continuously, reaching a maximum just before the fuel is exhausted.
Factors Affecting a Rocket’s Acceleration






