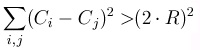where the last column contains 1. You can do so with the command backbone_chain =
zeros (N, 4); which creates a matrix with N rows and 4 columns initialized to all zeros.
You can set the fourth column to 1 with the command backbone_chain(:, 4) = 1; Now
you need to place the cartesian coordinates from the array to this matrix. You can do so with the
for loop below:
for i = 1:N
for j = 1:3
backbone_chain(i,j) = cartesian_coordinates((i-1) * 3 + j);
end;
end;
The cartesian coordinates you have just read will serve as a basis for performing rotations,
according to what method you choose to represent and manipulate the protein, as discussed in
class. The following guidelines should help you get started with either method:
If using the global coordinate (simple) approach, you can use the cartesian coordinates just read
as a basis to perform rotations on them. For the most interesting task of transforming atomic
positions, you simply need to iterate over the atoms affected by the transformation and
multiply their position with the transformation matrix. Say the position of atom i needs to be
transformed by your transformation matrix. You can do so by multiplying trans_mat with
backbone_chain(i, :) as in trans_mat * backbone_chain(i, :)'. Note that
the colon is very convenient as it gives an entire row or an entire column and that
backbone_chain(i, :)' gives you the transpose that is necessary for the multiplication
to be carried out.
If using the Denavit-Hartenberg local frames, you first need to extract the bond lengths and
angles, and the initial dihedral angles, from the cartesian coordinates. To do so, you can loop
over the atoms computing these values and storing them (for example in arrays named bonds,
angles, dihedrals). Once this is done, you have extracted a representation of the protein
in its internal coordinates and can discard the cartesian coordinates, or keep the coordinates
array to store the reconstructed protein after performing manipulations. The absolute
position/orientation of the protein is not important and can be ignored by assuming the anchor
atom rests at the origin and that the first bond angle and dihedral angle are both zero.
Remember you can perform rotations now by simply adding/subtracting from the dihedral
angles, but to recover the cartesian coordinates once the rotations are done you need to build a
chain of homogeneous transformations as discussed in class.
In any case, your transformation matrices need to have dimension 4x4 to work with homogeneous
coordinates. You can initialize an empty 4x4 matrix by writing trans_mat = zeros(4,4);.
Then you can set the elements of this matrix to what they should be for the particular method you
use. You can evaluate all the cosines and sines that you need in Matlab. Matlab offers you built-in
operations such as dot product or vector norm. Make sure that you understand these operations
before you apply them. Recall that you can rotate any bond except the peptide bond, which is
rigid.
Conduct the following rotations:
Rotate the dihedral bond between the N and CA of the last aminoacid by 30 degrees. Does the
structure change much? What atoms move in space as the result of this rotation? Please answer
Q1 .
Now choose any dihedral bond roughly in the middle of the protein and experiment with its
rotation until you reach a conformation that has steric clashes (atoms collide with one another).
Please answer Q3 and Q4 .
If you wish to visualize the resulting conformations in VMD, you simply have to produce a file
with the transformed coordinates. This file should be in ASCII (text) format and must have an
empty/dummy first line, and all atom coordinates following (for example all in a single line,
separated by spaces). You can save this file with ".crd" extension. Then, you can use the same
"backbone_native.pdb" file, and use VMD's option "Load data into molecule" to load your new
coordinates from the .crd file.
Ranking by Energy
Protein conformations are not only geometric objects but are characterized by energetic stability.
You have seen that there are many empirical ways to compute the potential energy of a
conformation. Functions such as CHARMM are very involved for the purpose of this assignment.
Therefore, let us not worry about all the energetic terms to be considered from the atomic
interactions. Consider only unfavorable interactions due to collisions between atoms, also referred
to as steric clashes. Think about a simple energy function that checks for steric clashes. Your
function should report high energies for conformations with collisions and low energies for
collision-free conformations. You can model each atom as a sphere with a certain radius known as
the Van der Waals (VDW) radius. Even though different atoms have different VDW radii, you can
assume that all atoms have the same radius of 1.7 A. To assist you in devising a function that
checks for collisions over all pairs of atoms, consider the following:
Figure 1.6.
For all different atoms i and j, make sure that the distance between their centers C is more than twice their radiuses. In this simple example we are using the same radius R.
Evaluating Rotations by Energy
Now think about the effect of the dihedral rotation of the last bond the energetic stability of the
new conformation. Please answer Q2 .
When you rotated a dihedral bond in the middle of the backbone until you reached a
conformation that had collisions, you verified the presence of steric clashes by visualizing the
conformation. You can quantify the presence of steric clashes now through your energy
function. Please answer Q5 .
Again, as in dihedral rotations, you are encouraged to use Matlab. After you have the cartesian
coordinates of the manipulated conformation, you can iterate over the atoms and check whether
they are in collision with one another. You can do this with a double loop. Assume that the radius
of every atom is the same, 1.7 A. In order to avoid reporting collisions for bonded atoms, you can
consider only pairs of atoms that are 4 positions apart. That is, check atom i with atom i+4 for a
possible steric clash.
For Submission
NOTE: remember that in order to open a .crd file in VMD (to attach it to a loaded structure) it has
to contain a dummy first line. If your implementation writes out ASCII coordinates, remember to
add an empty/dummy line at the beginning before opening with VMD. Please follow this list of
deliverables closely:
Q1 : Superimpose the conformation resulting from rotating the dihedral bond between the N and
CA of the last aminoacid by 30 degrees over the native backbone conformation. Prepare an image
that clearly shows which atoms' locations have changed. Submit this image.
Q2 : Now you need to quantify the energetic cost of rotating this dihedral bond by 30 degrees by
reporting whether this rotation causes any steric clashes. Please test your energy function on the
conformation you obtained from rotating the last dihedral bond by 30 degrees. Please report the
answer of your energy function. It should be compatible with what you can visualize from the
image you prepared above.
Q3 : Provide the index of the dihedral bond you need to rotate to generate a large scale motion
that results on collisions between atoms. Report on the amount of rotation that you need to
perform in order to obtain a conformation that contains steric clashes. Plot this conformation
superimposed on the native backbone conformation so as to show that it is very different from the
native. Render this image and submit it.
Q4 : Zoom in on that part of your conformation that contains collisions. Make sure that this
image clearly shows steric clashes and submit this image.
Q5 : Compute the energy of the above conformation with your energy function. Report the
answer that your energy function returns. Make sure that this answer reflects the fact that there
are steric clashes. Please provide the atomic distances for the atom pairs that your function
reports in collision.
Bonus : Upon a situation when the energy of the conformation resulting from a dihedral rotation
is high, how would you minimize the energy of this conformation? Provide a discussion and
pseudo-code on how you would perform the minimization.
Note: While you are welcome to use any programming language, please typeset your deliverables
and make sure that the quality of your images is good. You can use any visualization software to
produce your images. You are welcome to perform the asked rotations either through the Denavit-
Hartenberg derivation provided in our [PDF] document , or through simple rotations around arbitrary vectors. If you choose the latter, please note that there is a typo in the formula for the
rotation matrix Ri in Zhang-Kavraki, 2002 [PDF] on page 2: The second column, first row entry of this matrix is given as uxvy(1-cos(theta))+ vz sin(theta) , but it should be
vxvy(1-cos(theta))− vz sin(theta) .
1.3. Assignment 3: Inverse Kinematics*
Motivation for Inverse Kinematics in Proteins
One important application of inverse kinematics is in determining missing portions of protein
structure. We traditionally depend on experimental techniques to provide us with the picture of an
average structure for a protein. X-ray crystallography for example, relies on crystallizing proteins
and reporting the structure of the protein crystal within a certain resolution. One of the inherent
problems with X-ray crystallography is that mobile protein regions such as loops cause disorder in
the crystal and as a consequence, coordinates for the atoms of these mobile regions cannot be
reported. Often, in the PDB, crystallographically determined proteins are partially resolved, i.e. a
portion of the structure may be missing due to its intrinsic mobility. Even when experimental
techniques such as NMR and cryo-EM can report an average picture of the fully resolved protein,
the average structure reported is not indicative of the different conformations mobile regions can
assume inside our cells at room temperature.
The specific problem of completing a partially resolved protein structure by finding
conformations for its missing loop is known as the fragment completion or the loop closure
problem. Note that the loop closure problem is actually an inverse kinematics problem. Using
sequence information alone, i.e. knowing the aminoacid sequence of the missing loop, one can
generate starting loop conformations. The loop closure problem requires these loop conformations
to be geometrically constrained by attaching them to the portion of the protein structure that is
experimentally determined. Note that, as the picture below indicates, one can generate many loop
conformations in space through forward kinematics. One end of the loop can be attached to its
counterpart in the protein through translation alone. The other end however, needs to be attached
without breaking bonds or stretching bond angles. One way to do this is through inverse
kinematics; that is, knowing the goal position in space for the end of the loop, can we solve for the
dihedral DOFs of the loop conformation? This question can be answered by Inverse Kinematics
techniques.

Figure 1.7.
One "sticky" end of the loop can be attached to its stationary counterpart in the protein through translation. The other end needs to move towards its goal location by solving an Inverse Kinematics problem.
Inverse Kinematics for a Polypeptide Chain
Cyclic Coordinate Descent (CCD)
In this assignment you will complete a loop portion in the 1COA structure of the CI2 protein. X-
ray crystallography completely resolves the 1COA structure. However, even though a long loop
region from residue 34 to residue 46 is present in the native conformation of 1COA, an interesting
exercise is to pretend this loop region cannot be determined. Using an inverse kinematics
approach, you will sample many potential loops that can all complete the 1COA structure and
compare them to the native conformation obtained through X-ray crystallography. An important
question to answer is whether your loop closure algorithm can recover/predict the conformational
state of this loop region in CI2; that is, how different are your loops from the one in the native
conformation of CI2? You will implement a simple inverse kinematics technique, Cyclic
Coordinate Descent (CCD) as presented in [link]. For simplicity, you will work with the native
backbone of CI2, whose respective native coordinates you can also obtain from the
backbone_native.crd file.
Your task is to generate 10 different loops that all complete the protein structure of CI2 and
compare them to the native loop conformation. To do so, even though the native loop
conformation is given to you in the backbone.pdb file, you will pretend that the loop region from residue 34 to residue 46 is not resolved. You will generate different conformations for this loop
region by randomly sampling values for the dihedral of the loop, uniformly in the range [-PI, PI].
Then you will use the CCD algorithm described in [link] to steer these loop conformations to their goal/target location as specified by the coordinates of residue 46 in the native conformation of
CI2.
The Cyclic Coordinate Descent, as defined in [link], allows you to find the optimal dihedral angle for a dihedral bond by whose rotation a desired atom will get as close as possible to a target
position. To simplify this problem, you will not have target positions for the three atoms N, CA, C
as [link] does, but only on one atom, the C atom. This means that the equations you need to solve for the optimal dihedral rotation are going to be much simpler, with your distance measure S
defined as the Euclidean distance between current position M of atom C and its target position F.
Please address Q1 .
CCD for a Chain
You have noticed by now that CCD reports the angle by which to rotate a particular dihedral bond
so that the feature atom gets as close as possible to its target position. Consider a chain with the
feature atom at its end. As in real polypeptides, this chain does not contain only one dihedral
angle, but many. How would you use the CCD routine to solve for all the dihedrals of this chain so
that the final end of the chain reaches a target position? Please address Q2 . (Hint: You might consider solving for each dihedral one at a time, after you have imposed an order on the dihedrals
you are working with.)
For convenience, we will refer to the conformation of the chain where the atom reaches its target
position as the closure conformation. The problem you will address in this assignment is how to
obtain different closure conformations by solving for the dihedral DOFs of a chain in order to go
from a starting/initial/current conformation to a closure conformation. In order to generate closure
conformations, before solving for the dihedral DOFs through CCD for a chain, you need to
generate starting/initial conformations for the loop region of CI2. One way to do so is to generate
random angles for the dihedrals of the chain and then accumulate the respective transformation
matrices down the chain through Forward Kinematics, as you have done in Assignment 2. You are
not allowed to rotate only one dihedral bond to generate a random initial transformation. You
have to rotate all dihedral bonds of a chain by random angles in the interval [-PI, PI]. Please
answer Q3 .
Now it is time for you to put your pseudocode to the test. We first list the particular specifications
for the inverse kinematics problem you will solve in this assignment.
For this problem, you will steer the C atom of residue 46 of the loop region towards its target
position. We will refer to this atom as the feature atom.
We need to define the DOFs. As you will only generate closure conformations for the loop
region from residue 34 to residue 46, the only DOFs you can sample in the intial loop
conformations and solve for in the closure conformations are those of the loop region. Every
other dihedral you cannot change.
The CCD algorithm needs to have a measure of distance between the current position of the
feature atom and its target position. After you have generated initial conformations for the loop
region, the current position of the feature atom is position in space of the C atom of residue 46
in this initial conformation.
The target position of the feature atom will be its position as specified in the original (native)
conformation contained in the backbone_native.crd file.
Now we can put the pieces together: Generate an initial conformation by rotating the dihedrals
of the 34-46 loop region of CI2 with random angles sampled uniformly in the [-PI, PI] interval.
Solve for the dihedrals of the 34-46 region so that the C atom of aminoacid 46 in the initial
conformation you have just generated reaches its target position as specified by its position in
the native conformation in the backbone_native.crd file. Note that depending on the random
conformation you start with, it might be hard to steer atom C to reach its target position. After
applying the dihedrals you have solved for, you might need to do additional iterations to solve
for the dihedrals of the updated conformation, apply those and so on until the spatial constraint
for atom C is satisfied. To have a quantitative criterion for when atom C satisfies its spatial
constraint, you need to define a threshold parameter for S, as in [link]. Set this threshold criterion to 0.01 for this assignment. Please answer Q4 .
In this way, you will generate 10 closure conformations where the C atom of aminoacid 46 will be
in its target position, its position in the native conformation. It is interesting to note that the native
conformation itself is a closure conformation since it satisfies the spatial constraint on this atom.
Now you can quantify the similarity/difference between these 10 closure conformations and the
native conformation. As in assignment 1, you can compute the least RMSD of these 10 closure
conformations from the native. You can also compute the energy of each of these 10
conformations and the native. Please address Q5 and Q6 .
Setup with Matlab
Even though you are welcome to use any programming language to complete this assignment, we
suggest that you use Matlab due to its convenient matrix operations. For this assignment you will
need some basic trigonometry functions such as sine , cosine , tangent , and inverse
tangent/arctangent . You can find all these functions already implemented in Matlab. Please get familiar with their syntax by using the Help pages. Figure 1 captures the Help page for the
category of Functions By Category , subcategory Elementary Math . You need to read this
category to learn more on how to use these functions.
Figure 1.8.
Matlab Trigonometry
It is very important that you use the right arctangent implementation for this assignment. The
authors in [link] use the atan2 function as implemented in C . There is a similar function in Matlab . Please be careful to understand in what quadrant this function returns its output. You can
learn more about this function under the Help pages. Figure 2 captures the help page for this
function under the category of Functions By Category , subcategory Elementary Math , as part
of the Trigonometric functions.

Figure 1.9.
Matlab atan2 function
For Submission
Please follow this list closely.
Q1 : Please repeat the derivation in [link] with the simplification we made that only one atom is the one we want to to move to its target position. Typeset these derivations for submission.
Q2 : Please typeset your pseudocode for how you would iterate over a chain until the end of the
chain reaches its target position.
Q3 : Please provide pseudocode for how you would generate a random conformation for the 34-
46 region of the protein. Please generate 10 conformations in this way and visualize these
conformations through VMD, all superimposed over the native. Submit this image.
Q4 : Please plot all the final 10 conformations where the C atom of aminoacid 46 reaches its
target position. Plot these conformations over the native. Indicate where the C atom lies with a
VDW representation in red. Submit this image. (Note: remember that VMD requires a dummy
first line in .crd files, so add one if your code does not).
Q5 : Please compute the RMSD of the 10 closure conformations from the native. Please plot
these values and submit this plot. Please check the 10 closure conformations and the native
conformation for collisions with the energy function you implemented in assignment 2. Please
report the energetic scores of each conformation. Does the native conformation contain any
collisions? How do the other closure conformations compare to the native in terms of energy?
What can you conclude about your implementation of CCD to get a closure conformation with
regard to the energy of this closure conformation?
Q6 : The CCD algorithm does not take into consideration energetic constraints due to unfavorable
steric clashes. One way to impose energetic considerations is to discriminate against closure
conformations that contain steric clashes. You have already implemented a simplistic energy
function that can report the presence of collisions. Please provide pseudo-code on how you would
couple CCD with your energy function to report only closure conformations that do not contain
collisions.
Note: While you are welcome to use any programming language, please typeset your deliverables.
We encourage you to use Matlab. You may use any visualization software to produce your images.
References
1. A. A. Canutescu, and R. L. Dunbrack. (2003). Cyclic Coordinate Descent: A Robotics
Algorithm for Protein Loop Closure. [http://www.proteinscience.org/cgi/reprint/12/5/963].
Protein Science, 12, 963-972.
Solutions
Index
Symbols
α-complex, Computing the Alpha-Shape: Delaunay Triangulation
α-helices, Protein Structure
α-hull, Alpha-Shapes
α-shape, Computing the Alpha-Shape: Delaunay Triangulation
α-shapes, Alpha-Shapes
β-sheets,