receptor. This section will review the different receptor flexibility representations that have been
proposed to study receptor conformational changes in the context of structure based drug design.
A central paradigm which was used in the development of the first docking programs was the
lock-and-key model first described by Fischer [10] [link]. In this model the three dimensional structure of the ligand and the receptor complement each other in the same way that a lock
complements a key. However, further work confirmed that the lock-and-key model is not the most
correct description for ligand binding. A more accurate view of this process was first presented by
Koshland [11] [link] in the induced fit model. In this model the three dimensional structure of the ligand and the receptor adapt to each other during the binding process. It is important to note
that not only the structure of the ligand but also the structure of the receptor changes during the
binding process. This occurs because the introduction of a ligand modifies the chemical and
structural environment of the receptor. As a result, the unbound protein conformational substates,
corresponding to the low energy regions of the protein energy landscape are likely to change. The
induced fit model is supported by multiple observations in different proteins such as streptavidin,
HIV-1 protease, DHFR, aldose reductase and many others.
More information about some of these proteins and other proteins motions can be found at the
following links:
HIV Protease Database
DHFR the MOVIE homepage
Database of Macromolecular Movements
Although it has been clearly established that a protein is able to undergo conformational changes
during the binding process, most docking studies consider the protein as a rigid structure. The
reason for this crude approximation is the extraordinary increase in computational complexity that
is required to include the degrees of freedom of a protein in a modeling study. There is currently
no computationally efficient docking method that is able to screen a large database of potential
ligands against a target receptor while considering the full flexibility of both ligand and receptor.
In order for this process to become efficient, it is necessary to find a representation for protein
flexibility that avoids the direct search of a solution space comprised of thousands of degrees of
freedom. What follows is a brief review of the different representations that have been used to
incorporate protein flexibility in the modeling of protein/ligand interactions. A common theme
behind all these approaches is that the accuracy of the results is usually directly proportional to
the computational complexity of the representation. The different types of flexibility
representations models are grouped into categories that illustrate some of the key ideas that have
been presented in the literature in recent years. However it is important to note that the boundaries
between these categories are not rigid and in fact several of the publications referenced below
could easily fall in more than one category.
Flexibility Representations
Soft Receptors
Perhaps the simplest solution to represent some degree of receptor flexibility in docking
applications is the use of soft receptors. Soft receptors can be easily generated by relaxing the
high energy penalty that the system incurs when an atom in the ligand overlaps an atom in the
receptor structure. By reducing the van der Waals contributions to the total energy score the
receptor is in practice made softer, thus allowing, for example, a larger ligand to fit in a binding
site determined experimentally for a smaller molecule (see Figure 6). The rationale behind this
approach is that the receptor structure has some inherent flexibility which allows it to adapt to
slightly differently shaped ligands by resorting to small variations in the orientation of binding
site chains and backbone positions. If the change in the receptor conformation is small enough, it
is assumed that the receptor is capable of such a conformational change, given its large number of
degrees of freedom, even though the conformational change itself is not modeled explicitly. It is
also assumed that the change in protein conformation does not incur a sufficiently high energetic
penalty to offset the improved interaction energy between the ligand and the receptor. The main
advantage of using soft receptors is ease of implementation (docking algorithms stay unchanged)
and speed (the cost of evaluating the scoring function is the same as for the rigid case).
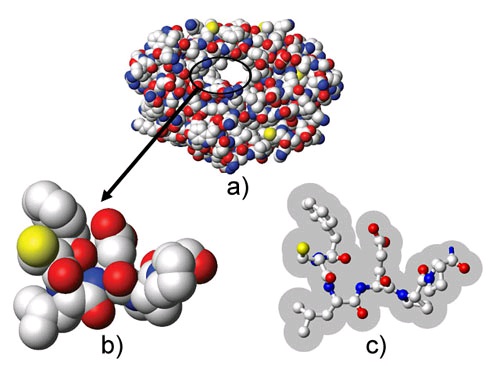
Figure 112.
a) Three dimensional van der Walls representation of a target receptor. b) Close up image of a section of the binding site. For the purposes of rigid protein docking, the receptor is commonly described by the union of the volumes occupied by its atoms. The steric collision of any atom of the candidate ligand with the atoms of the receptor will result in a high energetic penalty. c) Same section of the binding site as shown in b) but with reduced radii for the atoms in the receptor. This type of soft representation allows ligand atoms to enter the shaded area without incurring a high energetic penalty.
Another use of soft docking models is to improve convergence during energy minimization of the
complex by avoiding local minima. In the initial stages of the conformational search the ligand is
allowed to overlap with the receptor and nonbonded energy terms are modified to avoid high
energy gradients. During the course of the minimization the interactions are then gradually
restored to their original values simulating a ligand that is gradually exposed to the field of the
receptor. This allows initial ligand/receptor conformations, which due to steric clashes would
result in a very high energy penalty, to slowly adapt to each other in a complementary
conformation without overlaps. One potential pitfall of this approach is the possibility that the
ligand may become interlocked with the protein, leading to failure of the docking procedure.
Although the use of soft receptors presents a number of advantages such as ease of
implementation and computation speed, it also makes use of conformational and energetic
assumptions that are difficult to verify. This can easily result in errors, especially if the soft
region is made excessively large to account for larger conformational changes on the part of the
receptor.
Selection of Specific Degrees of Freedom
In order to reduce the complexity of modeling the very large dimensional space representing the
full flexibility of the protein, is it possible to obtain an approximate solution by selecting only a
few degrees of freedom to model explicitly. The degrees of freedom chosen usually correspond to
rotations around single bonds (see Figure 7). The reason for this choice is that these degrees of
freedom are usually considered the natural degrees of freedom in molecules. Rotations around
bonds lead to deviations from ideal geometry that result in a small energy penalty when compared
to deviations from ideality in bond lengths and bond angles. This assumption is in good agreement
with current modeling force fields such as CHARMM [12] [link] and AMBER [13] [link].
Selection of which torsional degrees of freedom to model is usually the most difficult part of this
method because it requires a considerable amount of a priori knowledge of alternative binding
modes for a given receptor. This knowledge usually is a result of the availability of experimental
structures obtained under different conditions or using different ligands. If multiple experimental
structures are not available some insight can be obtained from simulation methods such as Monte
Carlo (MC) or molecular dynamics (MD). The torsions chosen are usually rotations of aminoacid
side chains in the binding site of the receptor protein. It is also common to further reduce the
search space by using rotamer libraries for the aminoacid side chains
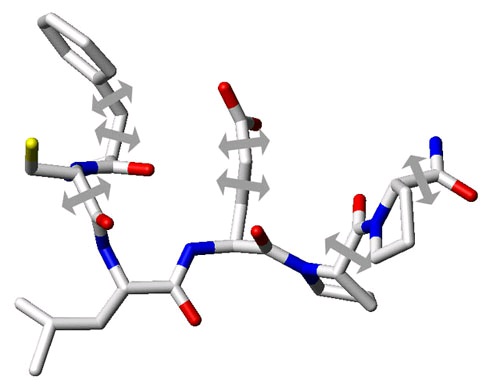
Figure 113.
Stick representation of the same binding site section as shown in Figure 1. In order to approximate the flexibility of the receptor it is possible to carefully select a few degrees of freedom. These are usually select torsional angles of sidechains in the binding site that have been determined to be critical in the induced fit effect for a specific receptor. In this example the selected torsional angles are represented by arrows.
An example of a program that takes the approach of selecting a few degrees of freedom to
represent protein flexibility is the program GOLD [14] [link]. In GOLD, Jones et al. use a genetic algorithm (GA) to dock a flexible ligand to a semi-flexible protein. GAs are an optimization
method that derives its behavior from a metaphor of the process of evolution. A solution to a
problem is encoded in a chromosome and a fitness score is assigned to it based on the relative
merit of the solution. A population of chromosomes then goes through a process of evolution in
which only the fittest solutions survive. This program takes into account not only the position and
conformation of the ligand but also the hydrogen bonding network in the binding site. This was
achieved by encoding orientation information for donor hydrogen atoms and acceptors in the GA
chromosome. This type of conformational information is very important because if the starting
point for a docking study is a rigid crystallographic structure, the orientations of hydroxyl groups
will be undetermined. Being able to model these orientations explicitly removes any bias that
might result from positioning hydroxyl groups based upon a known ligand. One limitation of this
work is that the binding site still remains essentially rigid because protein conformational changes
are limited to a few terminal bonds. This program performed very well for hydrophilic ligands but
encountered some difficulties when trying to dock hydrophobic ligands due to the reduced
contribution of hydrogen bonding to the binding process. More information about GOLD can be
found at the following link: http://www.ccdc.cam.ac.uk/prods/gold/
Multiple Receptor Structures
One possible way to represent a flexible receptor for drug design applications is the use of
multiple static receptor structures (see Figure 8). This concept is supported by the currently
accepted model that proteins in solution do not exist in a single minimum energy static
conformation but are in fact constantly jumping between low energy conformational substates. In
this way the best description for a protein structure is that of a conformational ensemble of
slightly different protein structures coexisting in a low energy region of the potential energy
surface. Moreover the binding process can be thought of as not exactly an induced fit model as
described by Koshland in 1958 [11] [link] but more like a selection of a particular substate from the conformational ensemble that best complements the shape of a specific ligand.
The use of multiple static conformations for docking gives rise to two critical questions. The first
question is: How can we obtain a representative subset of the conformational ensemble typical of
a given receptor? Currently there exist only a limited set of means to generate the three
dimensional structure of macromolecules. The structures can be determined experimentally either
from X-ray crystallography or NMR, or generated via computational methods such as Monte
Carlo or molecular dynamics simulations. Simulations typically use as a starting point a structure
determined by one of the experimental methods. Ideally we would like to use a sampling that
provides the most extensive coverage of the structure space. Comparisons done between
traditional molecular simulations and experimental techniques [15] [link], [16] [link] seem to indicate that X-ray crystallography and NMR structures seem to provide better coverage. However
this balance can potentially change due to advances in computational methods. Another limitation
in choosing data sources is availability. Although experimental data is preferable, the monetary
and time cost of determining multiple structures experimentally is significantly higher than
obtaining the same amount of data computationally. The second critical question is: What is the
best way of combining this large amount of structural information for a docking study? This
question also remains open. Current approaches use diverse ways of combining multiple
structures.

Figure 114.
Superposition of multiple conformers of the same binding site section as shown in Figure 1. As an alternative to considering the target protein as a single three dimensional structure, it is possible to combine information from multiple protein conformations in a drug design effort. These can be either considered individually as rigid representatives of the conformational ensemble or can be combined into a single representation that preserves the most relevant structural information.
One of the main advantages of using multiple structures instead of using a selection of degrees of
freedom to represent protein flexibility is that the flexible region is not limited to a specific small
region of the protein. Multiple structures allow the consideration of the full flexibility of the
protein without the exponential blow up in terms of computational cost that would derive from
including all the degrees of freedom of the protein. On the other hand, flexibility is modeled
implicitly and as such only a small fraction of the conformational space of the receptor is
represented. In addition, the method by which the multiple receptor structures are combined has a
drastic influence on the possible results of the docking computation.
Molecular Simulations
To simulate the binding process with as much detail as possible and avoid some of the limitations
of previous flexibility models one can use force field based atomistic simulation methods such as
Monte Carlo or molecular dynamics (see Figure 9). Whereas molecular dynamics applies the laws
of classical mechanics to compute the motion of the particles in a molecular system, Monte Carlo
methods are so called because they are based on a random sampling of the conformational space.
The main advantage of Monte Carlo or molecular dynamics flexibility representations in docking
studies is that they are very accurate and can model explicitly all degrees of freedom of the
system including the solvent if necessary. Unfortunately, the high level of accuracy in the
modeling process comes with a prohibitive computational cost. For example, in the case of
molecular dynamics, state of the art protein simulations can only simulate periods ranging from
10 to 100 ns, even when using large parallel computers or clusters. Given that diffusion and
binding of ligands takes place over a longer time span, it is clear that these simulations techniques
cannot be used as a general method to screen large databases of compounds in the near future. It is
however possible to carry out approximations that reduce the computational expense and lead to
insights that would be impossible to gain using less flexible receptor representations. The cost of
carrying out the computational approximations is usually a loss in accuracy.
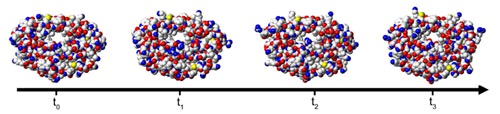
Figure 115.
Molecular simulations can give a description of the full protein flexibility as it interacts with a ligand. Molecular dynamics applies the laws of classical mechanics to compute the motion of particles in a molecular system. Alternatively, the different conformational snapshots obtained at times t 0 , t 1 , etc., can be used as multiple protein structures representing the conformational ensemble.
Collective Degrees of Freedom
An alternative representation for protein flexibility is the use of collective degrees of freedom.
This approach enables the representation of full protein flexibility, including loops and domains,
without a dramatic increase in computational cost. Collective degrees of freedom are not native
degrees of freedom of molecules. Instead they consist of global protein motions that result from a
simultaneous change of all or part of the native degrees of freedom of the receptor.
Collective degrees of freedom can be determined using different methods. One method is the
calculation of normal modes for the receptor [17] [link]. Normal modes are simple harmonic oscillations about a local energy minimum, which depends on the structure of the receptor and the
energy function. For a purely harmonic energy function, any motion can be exactly expressed as a
superposition of normal modes. In proteins, the lowest frequency modes correspond to delocalized
motions, in which a large number of atoms oscillate with considerable amplitude. The highest
frequency motions are more localized such as the stretching of bonds. By assuming that the
protein is at an energy minimum, we can represent its flexibility by using the low frequency
normal modes as degrees of freedom for the system. Zacharias and Sklenar [18] [link] applied a method similar to normal mode analysis to derive a series of harmonic modes that were used to
account for receptor flexibility in the binding of a small ligand to DNA. This in practice reduced
the number of degrees of freedom of the DNA molecule from 822 (3 × 276 atoms – 6) to
approximately 5 to 40.
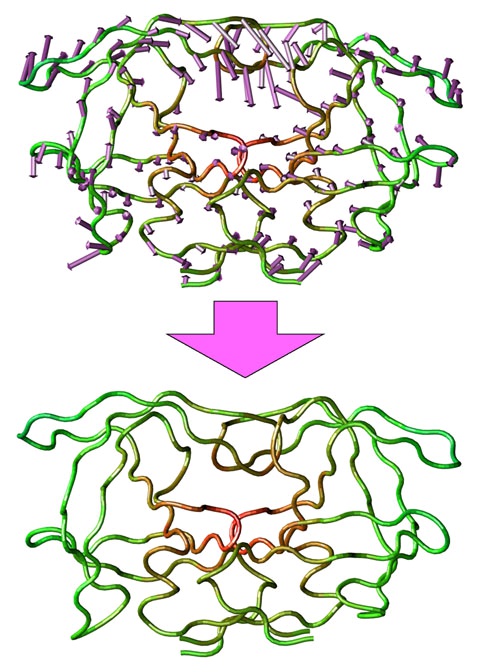
Figure 116.
Representation of a collective degree of freedom for HIV-1 protease. Full protein flexibility can be represented in a low dimensional space using collective degrees of freedom. One method to obtain these is Principal Component Analysis. Principal components
correspond to a concerted motion of the protein. The first principal component for HIV-1 protease is indicated by the arrows (top). By following this collective degree of freedom it is possible to generate alternative conformations for the receptor (bottom).
An alternative method of calculating collective degrees of freedom for macromolecules is the use
of dimensional reduction methods. The most commonly used dimensional reduction method for
the study of protein motions is principal component analysis (PCA). This method was first applied
by Garcia [19] [link] in order to identify high-amplitude modes of fluctuations in macromolecular dynamics simulations. It has also been used to identify and study protein conformational
substates, as a possible method to extend the timescale of molecular dynamics simulations and as
a method to perform conformational sampling. In the next module, we present a protocol [20]
[link] based on PCA to derive a reduced basis representation of protein flexibility that can be used to decrease the complexity of modeling protein/ligand interactions. The most significant principal
components have a direct physical interpretation. They correspond to a concerted motion of the
protein where all the atoms move in specific spatial directions and with fixed ratios in overall
displacement. An example is provided in Figure 10 where the directions and ratios are indicated
by the direction and size of the arrows, respectively. By considering only the most significant
principal components as the valuable degrees of freedom of the system, it is possible to cut down
an initial search space of thousands of degrees of freedom to less than fifty. This is achievable
because the fifty most significant principal components usually account for 80-90% of the overall
conformational variance of the system. The PCA approach avoids some of the limitations of
normal modes such as deficient solvent modeling and existence of multiple energy minima during
a large motion. The last limitation contradicts the initial assumption of a single well energy
potential.
Recommended Reading and Resources:
A review of flexible receptor methods, as of 2003: Teodoro, M.L. and L.E. Kavraki. [HTML].
(2003). Conformational Flexibility Models for the Receptor in Structure Based Drug Design.
Current Pharmaceutical Design, 9, 1635-1648.
A comprehensive overview of existing docking software, as of 2006: Sousa, S.F., Pedro
Fernandes A., and Ramos, M. J. [HTML]. (2006). Protein-ligand docking: Current status and future challenges. Proteins: Structure, Function, and Bioinformatics, 65(1) 15-26.
References
1. Eldridge, M.D., C.W. Murray, T.R. Auton, G.V. Paolini, and R.P. Mee. (1997). Empirical
Scoring Functions. I. The Development of a Fast, Fully Empirical Scoring Function to
Estimate the Binding Affinity of Ligands in Receptor Complexes. Journal of Computer-Aided
Molecular Design, 11, 425-445.
2. Boehm, H-J. (1994). The Development of a Simple Empirical Scoring Function to Estimate the
Binding Constant for a Protein-Ligand Complex of Known Three-Dimensional Structure.
Journal of Computer-Aided Molecular Design, 8, 243-256.
3. Muegge, I. and Y.C. Martin. (1999). A General and Fast Scoring Function for Protein-Ligand
Interactions: A Simplified Potential Approach. Journal of Medicinal Chemistry, 42, 791-804.
4. Gohlke, H., M. Hendlich, and G. Klebe. (2000). Knowledge Based Scoring Function to Predict
Protein-Ligand Interactions. Journal of Molecular Biology, 295, 337-356.
5. Morris, G.M., et al. (1998). Automated docking using a Lamarckian genetic algorithm and an
empirical binding free energy function. Journal of Computational Chemistry, 19, 1639-1662.
6. Kramer, B., M. Rarey, and T. Lengauer. (1999). Evaluation of the FLEXX incremental
construction algorithm for protein-ligand docking. Proteins, 37, 228-241.
7. Rarey, M., S. Wefing, and T. Lengauer. (1996). Placement of Medium-Sized Molecular
Fragments Into Active Sites of Proteins. Journal of Computer-Aided Molecular Design, 10,
41-54.
8. Kuntz, I.D., J.M. Blaney, S.J. Oatley, R. Langridge, and T.E. Ferrin. (1982). A Geometric
Approach to Macromolecule-Ligand Interactions. Journal of Molecular Biology, 18, 1175-
1189.
9. Ewing, T.J.A. and I.D. Kuntz. (1997). Critical evaluation of search algorithms for automated
molecular docking and database screening. Journal of Computational Chemistry, 18, 1175-
1189.
10. Fischer, E. (1894). Einfluss der Configuration auf die Wirkung der Enzyme. Ber. Dtsch. Chem.
Ges. , 27, 2985.
11. Koshland D.E. (1958). Application of a theory of enzyme specificity to protein synthesis.
Proceedings of the National Academy of Sciences USA, 44(2), 98-104.
12. MacKerell, A.D. et al. (1998). All-atom empirical potential for molecular modeling and
dynamics studies of proteins. J. Phys. Chem. B, 102, 3586-3616.
13. Cornell, W.D., et al. (1995). A second generation force field for the simulation of proteins and
nucleic acids. J. Am. Chem. Soc. , 117, 5179-5197.
14. Jones, G., et al. (1997). Development and validation of a genetic algorithm for flexible
docking. J Mol Biol, 267(3), 727-748.
15. Clarage, J.B., et al. (1995). A sampling problem in molecular dynamics simulations of
macromolecules. Proceedings of the National Academy of Sciences USA, 92(8), 3288-3292.
16. Philippopoulos, M. and C. Lim. (1999). Exploring the dynamic information content of a
protein NMR structure: comparison of a molecular dynamics simulation with the NMR and X-
ray structures of Escherichia coli ribonuclease. HI Proteins, 36(1), 87-110.
17. Levy, R.M. and M. Karplus. (1979). Vibrational Approach to the Dynamics of an alpha-Helix.
Biopolymers, 18, 2465-2495.
18. Zacharias, M. and H. Sklenar. (1999). Harmonic Modes as Variables to Approximately
Account for Receptor Flexibility in Ligand-Receptor Docking Simulations: Application to
DNA Minor Groove Ligand Complex.








