The velocity to reach opposite point of the stream
The angle at which boat sails to reach the opposite point is :
This expression points to a certain limitation with respect to velocities of boat and stream. If
velocity of boat in still water is equal to the velocity of stream, then
⇒ θ = 900
It means that boat has to sail in the direction opposite to the stream to reach opposite point. This is

an impossibility from the point of physical reality. Hence, we can say that velocity of boat in still
water should be greater than the velocity of stream ( vAB > vB ) in order to reach a point opposite to the point of sailing.
In any case, if vAB < vB , then the boat can not reach the opposite point as sine function can not be greater than 1.
Shortest path
The magnitude of linear distance covered by the boat is given by :
()
It is evident from the equation that linear distance depends on the drift of the boat, “x”. Thus,
shortest path corresponds to shortest drift. Now, there are two situations depending on the relative
magnitudes of velocities of boat and stream.
We should be aware that though the perpendicular distance to stream (width of the river) is the
shortest path, but boat may not be capable to follow this shortest path in the first place.
1: vAB > vB
We have seen that when stream velocity ( vB ) is less than the velocity of boat in still water, the
boat is capable to reach the opposite point across the stream. For this condition, drift (x) is zero
and represents the minimum value. Accordingly, the shortest path is :
()
s min = d
The boat needs to sail upstream at the specified angle. In this case, the resultant velocity is
directed across the river in perpendicular direction and its magnitude is given by :





Figure 3.31. Resultant velocity
The boat moves perpendicular to stream.
()
The time taken to cross the river is :
()
2: vAB < vB
In this case, the boat is carried away from the opposite point in the direction of stream. Now, the
drift “x” is given as :
For minimum value of “x”, first time derivative of “x” is equal to zero,
()
We need to find minimum drift and corresponding minimum length of path, subject to this
condition.
Motion of an object in a medium
We have discussed the motion in the specific reference of boat in water stream. However, the
consideration is general and is applicable to the motion of a body in a medium. For example, the
discussion and analysis can be extended to the motion of an aircraft, whose velocity is modified
by the motion of the wind.
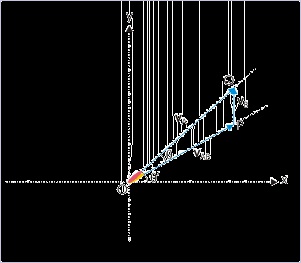


Example 3.22.
Problem : An aircraft flies with a wind velocity of 200√2 km/hr blowing from south. If the
relative velocity of aircraft with respect to wind is 1000 km/hr, then find the direction in
which aircraft should fly such that it reaches a destination in north – east direction.
Solution : The figure here shows the velocities. OP denotes the velocity of the aircraft in the
still air or equivalently it represents the relative velocity of aircraft with respect to air in
motion; PQ denotes the velocity of the wind and OQ denotes the resultant velocity of the
aircraft. It is clear that the aircraft should fly in the direction OP so that it is ultimately led to
follow the north-east direction.
We should understand here that one of the velocities is resultant velocity of the remaining two
velocities. It follows then that three velocity vectors are represented by the sides of a closed
triangle.
Figure 3.32. Motion of an aircraft
The aircraft flies such a way that it keeps a north – east course.
We can get the direction of OP, if we can find the angle “θ”. The easiest technique to
determine the angle between vectors composing a triangle is to apply sine law,
Putting values, we have :
θ = sin – 1 ( 0.2 )
Hence the aircraft should steer in the direction, making an angle with east as given by :
θ ′ = 450 − sin − 1 ( 0.2 )
3.6. Resultant motion (application)*
Questions and their answers are presented here in the module text format as if it were an extension
of the treatment of the topic. The idea is to provide a verbose explanation, detailing the
application of theory. Solution presented is, therefore, treated as the part of the understanding
process – not merely a Q/A session. The emphasis is to enforce ideas and concepts, which can not
be completely absorbed unless they are put to real time situation.
Representative problems and their solutions
We discuss problems, which highlight certain aspects of the study leading to the resultant
velocity. The questions are categorized in terms of the characterizing features of the subject
matter :
Velocity of the object
Time to cross the stream
Multiple references
Minimum time, distance and speed
Velocity of the object
Example 3.23.
Problem : A person can swim at 1 m/s in still water. He swims to cross a river of width 200 m
to a point exactly opposite to his/her initial position. If the water stream in river flows at 2 m/s
in a linear direction, then find the time taken (in seconds) to reach the opposite point.
Solution : Let the direction of stream be x-direction and the direction across stream be y-
direction. Let us also denote person with “A” and water stream with “B”.
To reach the point across, the person has to swim upstream at an angle such that the velocity
of the person with respect to ground( v A ) is across the direction of water stream. The
situation is shown in the figure.
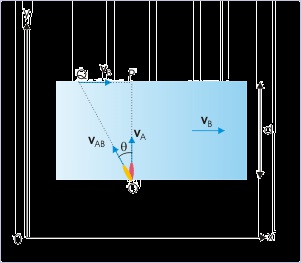


Figure 3.33. Relative velocity
Here,
From the ΔOAB,
It is clear from the denominator of the expression that for finite time, OB > AB. From the
values as given in the question, OB < AB and the denominator becomes square root of
negative number. The result is interpreted to mean that the physical event associated with the
expression is not possible.The swimmer, therefore, can not reach the point, which is exactly
opposite to his position. The speed of the swimmer should be greater than that of the stream to
reach the point lying exactly opposite.
Note that we had explained the same situation in the module on the subject with the help of
the value of "sinθ", which can not be greater than 1. We have taken a different approach here
to illustrate the same limitation of the swimmer's ability to cross the water stream, showing
that the interpretation is consistent and correct.
Example 3.24.
Problem : The direction of water stream in a river is along x – direction of the coordinate
system attached to the ground. A swimmer swims across the river with a velocity (
0.8 i + 1.4 j ) m/s, as seen from the ground. If the river is 70 m wide, how long (in seconds)
does he take to reach the river bank on the other side ?
Solution : We recognize here that the given velocity represents the resultant velocity ( v A ) of
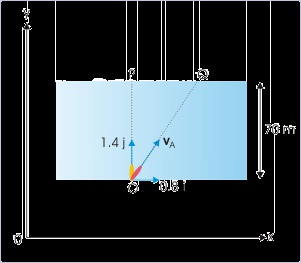




the swimmer (A). The time to reach the river bank on the other side is a function of
component velocity in y-direction.
Figure 3.34. Relative velocity
Here,
Example 3.25.
Problem : A person can swim at a speed “u” in still water. He points across the direction of
water stream to cross a river. The water stream flows with a speed “v” in a linear direction.
Find the direction in which he actually swims with respect to the direction of stream.
Solution : Let the direction of stream be x-direction and the direction across stream be y-
direction. Let us also denote person with "A" and water stream with “B”.
Here,
Using equation, v AB = v A – v B ,
From the figure,
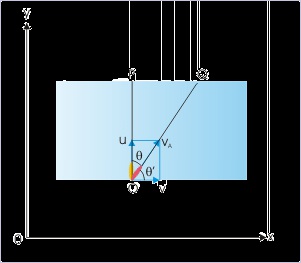




Figure 3.35. Relative velocity
The direction in which he actually swims with respect to the direction of stream is
Time to cross the river
Example 3.26.
Problem : A person can swim at a speed 1 m/s in still water. He swims perpendicular to the
direction of water stream, flowing at the speed 2 m/s. If the linear distance covered during the
motion is 300 m, then find the time taken to cross the river.
Solution : Let the direction of stream be x-direction and the direction across stream be y-
direction. Let us also denote ground person with "A" and water stream with “B”. This is
clearly the situation corresponding to the least time for crossing the river.
Here,
We note here that the perpendicular linear distance i.e. the width of river is not given. Instead,
the linear distance covered during the motion is given. Hence, we need to find the resultant
speed in the direction of motion to find time. Using equation for the resultant velocity,
From the figure, we have :



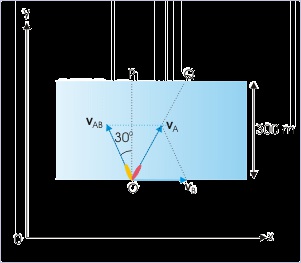
Figure 3.36. Relative velocity
Example 3.27.
Problem : A person can swim at a speed of √3 m/s in still water. He swims at an angle of
120° from the stream direction while crossing a river. The water stream flows with a speed of
1 m/s. If the river width is 300 m, how long (in seconds) does he take to reach the river bank
on the other side ?
Solution : Let the direction of stream be x-direction and the direction across stream be y-
direction. Here, we need to know the component of the resultant velocity in the direction
perpendicular to the stream.
Figure 3.37. Relative velocity



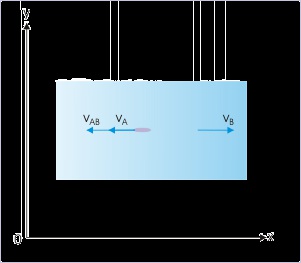
This approach, however, would be tedious. We shall use the fact that the component of " v A "
in any one of the two mutually perpendicular directions is equal to the sum of the components
of v A B and v B in that direction.
Thus, time taken to cross the river is :
Multiple references
Example 3.28.
Problem : A boat, capable of sailing at 2 m/s, moves upstream in a river. The water stream
flows at 1 m/s. A person walks from the front end to the rear end of the boat at a speed of 1
m/s along the linear direction. What is the speed of the person (m/s) with respect to ground ?
Solution : Let the direction of stream be x-direction and the direction across stream be y-
direction. We further denote boat with “A”, stream with “B”, and person with “C”.
We shall work out this problem in two parts. In the first part, we shall find out the velocity of
boat (A) with respect to ground and then we shall find out the velocity of person (C) with
respect to ground.
Here,



Figure 3.38. Relative velocity
The velocity of boat with respect to ground is equal to the resultant velocity of the boat as
given by :
For the motion of person and boat, the velocity of the person with respect to ground is equal to
the resultant velocity of (i) velocity of the person (C) with respect to boat (A) and (ii) velocity
of the boat (A) with respect to ground. We note here that relative velocity of person with
respect to boat is given and that we have already determined the velocity of boat (A) with
respect to ground in the earlier step. Hence,
Figure 3.39. Relative velocity
Minimum time, distance and speed
Example 3.29.
Problem : A boy swims to reach a point “Q” on the opposite bank, such that line joining
initial and final position makes an angle of 45 with the direction perpendicular to the stream
of water. If the velocity of water stream is “u”, then find the minimum speed with which the
boy should swim to reach his target.
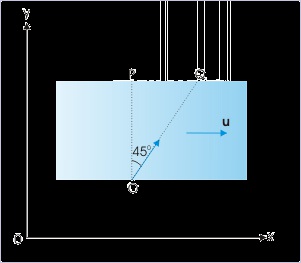
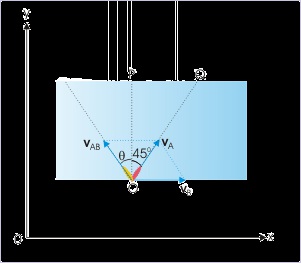

Figure 3.40. Crossing a river
The boy swims to reach point “Q”.
Solution : Let “A” and “B” denote the boy and the stream respectively. Here, we are required
to know the minimum speed of boy, vAB (say “v”) such that he reaches point “Q”. Now, he can
adjust his speed with the direction he swims. Let the boy swims at an angle “θ” with a speed
“v”.
Figure 3.41. Crossing a river
The boy swims to reach point “Q”.
Looking at the figure, it can be seen that we can make use of the given angle by taking
trigonometric ratio such as tangent, which will involve speed of boy in still water (v) and the
speed of water stream (u). This expression may then be used to get an expression for the
minimum speed as required.
The slope of resultant velocity, v A , is :
⇒ vAx = vAx



Now, the components of velocity in “x” and “y” directions are :
vAx = u – v sin θ
vAy = v cos θ
Putting in the equation we have :
u – v sin θ = v cos θ
Solving for “v”, we have :
The velocity is minimum for a maximum value of denominator. The denominator is
maximum for a particular value of the angle, θ; for which :
⇒ cos θ – sin θ = 0
⇒ tan θ = 1
⇒ θ = 450
It means that the boy swims with minimum speed if he swims in the direction making an
angle of 45 with y-direction. His speed with this angle is :
Example 3.30.
Problem : A boat crosses a river in minimum time, taking 10 minutes during which time the
it drifts by 120 m in the direction of stream. On the other hand, boat takes 12.5 minutes while
moving across the river. Find (i) width of the river (ii) velocity of boat in still water and (iii)
speed of the stream.
Solution : There are three pieces of information about "minimum time", "drift" and "time
along shortest path". Individually each of these values translate into three separate equations,
which can be solved to find the required values.
The boat takes minimum time, when it sails in the direction perpendicular to the stream
(current). The time to cross the river is given by dividing width with component of resultant
velocity ( vAy ). The boat, in this case, sails in the perpendicular direction. Hence, the
component of resultant velocity is equal to the velocity of boat in still water ( v AB ). The time
to cross the river in this case is :
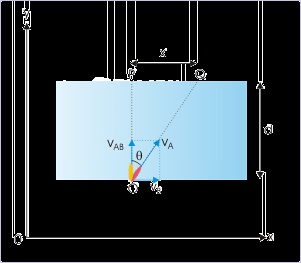



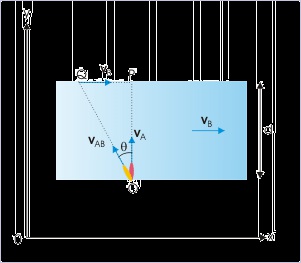
Figure 3.42. Crossing a river
The swims towards “P”.
d = 10 vAB
The drift in this time is given by :
x = vB t min
Putting values,
Now we need to use the information on shortest path. It is given that the boat moves across
stream in 12.5 minutes. For this boat has to sail upstream at certain angle. The resultant speed
is given by :
Figure 3.43. Crossing a river
The swims towards “P”.




and the time taken is :
Substituting for “d” and “ v B ” and squaring on both sides, we have :
( v 2 AB − 122 ) 12.52 = d 2 = 102 v 2 AB
v 2 AB ( 12.52 − 102 ) = 122 x 12.52
and
Solutions
Chapter 4. Accelerated motion in two dimensions
4.1. Projectile motion
Projectile motion*
Projectile motion is a special case of two dimensional motion with constant acceleration. Here,
force due to gravity moderates linear motion of an object thrown at certain angle to the vertical
direction. The resulting acceleration is a constant, which is always directed in vertically
downward direction.
The projectile motion emphasizes one important aspect of constant acceleration that even constant
acceleration, which is essentially unidirectional, is capable to produce two dimensional motion.
The basic reason is that force and initial velocity of the object are not along the same direction.
The linear motion of the projected object is continuously worked upon by the gravity, which
results in the change of both magnitude and direction of the velocity. A change in direction of the
velocity ensures that motion is not one dimensional.
The change in magnitude and direction of the velocity is beautifully managed so that time rate of
change in velocity is always directed in vertically downward direction i.e. in the direction of
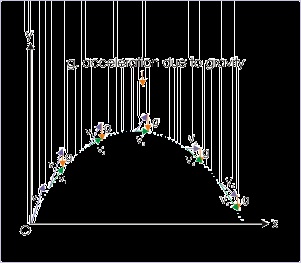
gravity. This aspect is shown qualitatively for the motion in the figure below as velocity change
successively at the end of every second from v 1 to v 2 to v 3 and so on….. by exactly a vector, whose magnitude is equal to acceleration due to gravity “g”.
Figure 4.1. Projectile motion
Velocity of the projectile changes by acceleration vector in unit time.
Force(s) in projectile motion
Flight of base ball, golf ball etc. are examples of projectile motion. In these cases, the projectile is
projected with certain force at certain angle to vertical direction. The force that initiates motion is
a contact force. Once the motion of the ball is initiated, the role of contact force is over. It does
not subsequently affect or change the velocity of the ball as the contact is lost.
In order to emphasize, we restate three important facts about projectile motion. First, we need to
apply force at the time of projection. This force as applied by hand or by any other mechanical
device, accelerates projectile briefly till it is in contact with "thrower". The moment the projectile
is physically disconnected with the throwing device, it moves with a velocity, which it gained
during brief contact period. The role of force responsible for imparting motion is over. Second,
motion of projectile is maintained if there is no net external force (Newton's laws of motion). This
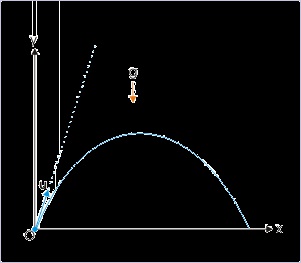
would be the case for projection in force free space. The projectile is initiated into the motion with
certain initial velocity, say u. Had there been no other force(s), then the ball would have moved
along the dotted straight line (as shown in figure below) and might have been lost in to the space.
Figure 4.2. Projectile motion
Path of a projectile projected at an angle with horizontal direction.
Third, the projectile, once out in the space, is acted upon by the force due to gravity and air
resistance. We, however, neglect the effect of air resistance for the time being and confine our
study of the motion which is affected by force d





















































