



The numerator of the above is maximum when the angle is 90°.
We should note that the formula of maximum height for a projectile projected at certain angle
represents the maximum height of the projectile for the given angle of projection and spped. The
question here, however, refers to maximum height for any angle of projection at given speed of
projection. As such, we should consider an angle of projection for which projectile reaches the
greatest height. This point should be kept in mind.
Hence, option (b) is correct.
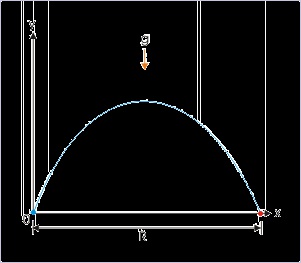
Range of projectile, R
The horizontal range is the displacement in horizontal direction. There is no acceleration involved
in this direction. Motion is an uniform motion. It follows that horizontal range is transversed with
the horizontal component of the projection velocity for the time of flight (T). Now,
Figure 4.17. Projectile motion
The range of a projectile
where “T” is the time of flight. Putting expression for the time of flight,
()
Horizontal range, like time of flight and maximum height, is greater for greater projection speed.



For projection above ground surface, the range of the angle of projection with respect to
horizontal direction, θ, is 0° ≤ θ ≤ 90° and the corresponding range of 2θ is 0° ≤ 2θ ≤ 180°. The
“sin 2θ”, as appearing in the numerator for the expression of the horizontal range, is an increasing
function for 0° ≤ θ ≤ 45° and a decreasing function for 45° ≤ θ ≤ 90° . For θ = 45°, sin 2θ = sin
90° = 1 (maximum).
In the nutshell, the range,R, increases with increasing angle of projection for 0° ≤ θ < 45°; the
range,R, is maximum when θ = 45°; the range,R, decreases with increasing angle of projection for
45° < θ ≤ 90°.
The maximum horizontal range for a given projection velocity is obtained for θ = 45° as :
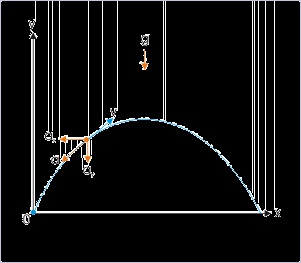
There is an interesting aspect of “sin 2θ” function that its value repeats for component angle i.e
(90° – θ). For, any value of θ,
Figure 4.18. Horizontal range
Horizontal range is same for a pair of projection angle.
It means that the range of the projectile with a given initial velocity is same for a pair of
projection angles θ and 90° – θ. For example, if the range of the projectile with a given initial
velocity is 30 m for an angle of projection, θ = 15°, then the range for angle of projection, θ = 90°
- 15° = 75° is also 30m.
Equation of projectile motion and range of projectile
Equation of projectile motion renders to few additional forms in terms of characteristic features of
projectile motion. One such relation incorporates range of projectile (R) in the expression. The







equation of projectile motion is :
The range of projectile is :
Solving for u 2 ,
Substituting in the equation of motion, we have :
It is a relatively simplified form of equation of projectile motion. Further, we note that a new
variable “R” is introduced in place of “u”.
Exercise 13.
If points of projection and return are on same level and air resistance is neglected, which of the
following quantities will enable determination of the range of the projectile (R) :
(a) horizontal component of projection velocity
(b) projection speed and angle of projection
(c) vertical component of projection velocity
(d) speed at the highest point
The horizontal range is determined using formulae,
Hence, horizontal range of the projectile can be determined when projection speed and angle of
projection are given. The inputs required in this equation can not be made available with other
given quantities.
Hence, option (b) is correct.
Note : Horizontal range (R) unlike time of flight (T) and maximum height (H), depends on both






vertical and horizontal motion. This aspect is actually concealed in the term "sin2 θ ". The
formula of horizontal range (R) consists of both "u sin θ " (for vertical motion) and "u cos θ " (for horizontal motion) as shown here :
Exercise 14.
A projectile is thrown with a velocity
. Then, the range of the projectile (R) is :
We shall not use the standard formulae as it would be difficult to evaluate angle of projection
from the given data. Now, the range of the projectile (R) is given by :
R = ux T
Here,
We need to know the total time of flight, T. For motion in vertical direction, the vertical
displacement is zero. This consideration gives the time of flight as :
Hence, range of the flight is :
⇒ R = ux T = 6 X 4 = 24
Hence, option (c) is correct.
Impact of air resistance
We have so far neglected the effect of air resistance. It is imperative that if air resistance is
significant then the features of a projectile motion like time of flight, maximum height and range
are modified. As a matter of fact, this is the case in reality. The resulting motion is generally
adversely affected as far as time of flight, maximum height and the range of the projectile are
concerned.
Air resistance is equivalent to friction force for solid (projectile) and fluid (air) interface. Like
friction, air resistance is self adjusting in certain ways. It adjusts to the relative speed of the
projectile. Generally, greater the speed greater is air resistance. Air resistance also adjusts to the
direction of motion such that its direction is opposite to the direction of relative velocity of two
entities. In the nutshell, air resistance opposes motion and is equivalent to introducing a variable
acceleration (resistance varies with the velocity in question) in the direction opposite to that of
velocity.
For simplicity, if we consider that resistance is constant, then the vertical component of
acceleration ( a y ) due to resistance acts in downward direction during upward motion and adds to
the acceleration due to gravity. On the other hand, vertical component of air resistance acts in
upward direction during downward motion and negates to the acceleration due to gravity. Whereas
the horizontal component of acceleration due to air resistance ( a x )changes the otherwise uniform
motion in horizontal direction to a decelerated motion.
Figure 4.19. Projectile motion with air resistance
Acceleration due to air resistance
With air resistance, the net or resultant acceleration in y direction depends on the direction of
motion. During upward motion, the net or resultant vertical acceleration is " – g – a y ". Evidently, greater vertical acceleration acting downward reduces speed of the particle at a greater rate. This,
in turn, reduces maximum height. During downward motion, the net or resultant vertical
acceleration is " – g + a y ". Evidently, lesser vertical acceleration acting downward increases speed of the particle at a slower rate. Clearly, accelerations of the projectile are not equal in
upward and downward motions. As a result, projection velocity and the velocity of return are not
equal.
On the other hand, the acceleration in x direction is " – a x ". Clearly, the introduction of
horizontal acceleration opposite to velocity reduces the range of the projectile (R).
Situations involving projectile motion
There are classic situations relating to the projectile motion, which needs to be handled with
appropriate analysis. We have quite a few ways to deal with a particular situation. It is actually the
nature of problem that would determine a specific approach from the following :
1. We may approach a situation analyzing as two mutually perpendicular linear motions. This is
the basic approach.
2. In certain cases, the equations obtained for the specific attributes of the projectile motion such
as range or maximum height can be applied directly.
3. In some cases, we would be required to apply the equation of path, which involves
displacements in two directions (x and y) simultaneously in one equation.
4. We always have the option to use composite vector form of equations for two dimensional
motion, where unit vectors are involved.
Besides, we may require combination of approached as listed above. In this section, we shall study
these classic situations involving projectile motion.
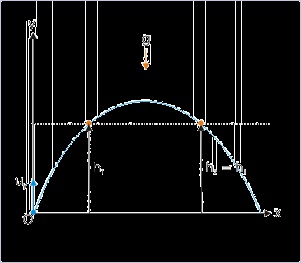
Clearing posts of equal height
A projectile can clear posts of equal height, as projectile retraces vertical displacement attained
during upward flight while going down. We can approach such situation in two alternative ways.
The equation of motion for displacement yields two values for time for a given vertical
displacement (height) : one corresponds to the time for upward flight and other for the downward
flight as shown in the figure below. Corresponding to these two time values, we determine two
values of horizontal displacement (x).
Figure 4.20. Projectile motion
The projectile retraces vertical displacement.
Alternatively, we may use equation of trajectory of the projectile. The y coordinate has a quadratic








equation in "x". it again gives two values of "x" for every value of "y".
Example 4.9.
Problem : A projectile is thrown with a velocity of
m/s and at an angle 45° with the
horizontal. The projectile just clears two posts of height 30 m each. Find (i) the position of
throw on the ground from the posts and (ii) separation between the posts.
Solution : Here, we first use the equation of displacement for the given height in the vertical
direction to find the values of time when projectile reaches the specified height. The equation
of displacement in vertical direction (y) under constant acceleration is a quadratic equation in
time (t). Its solution yields two values for time. Once two time instants are known, we apply
the equation of motion for uniform motion in horizontal direction to determine the horizontal
distances as required. Here,
Horizontal motion (refer the figure) :
Thus, projectile needs to be thrown from a position 50 m from the pole. Now,
Hence, separation, d, is :
Alternatively
Equation of vertical displacement (y) is a quadratic equation in horizontal displacement (x).
Solution of equation yields two values of "x" corresponding to two positions having same
elevation. Now, equation of projectile is given by :
Putting values,
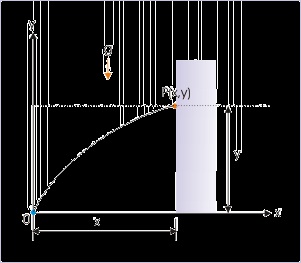

Hitting a specified target
An archer aims a bull’s eye; a person throws a pebble to strike an object placed at height and so
on. The motion involved in these situations is a projectile motion – not a straight line motion. The
motion of the projectile (arrow or pebble) has an arched trajectory due to gravity. We need to aim
higher than line of sight to the object in order to negotiate the loss of height during flight.
Figure 4.21. Projectile motion
The projectile hits the wall at a given point.
Hitting a specified target refers to a target whose coordinates (x,y) are known. There are two
different settings of the situation. In one case, the angle of projection is fixed. We employ
equation of the projectile to determine the speed of projectile. In the second case, speed of the
projectile is given and we need to find the angle(s) of projection. The example here illustrates the
first case.
Example 4.10.
Problem : A projectile, thrown at an angle 45° from the horizontal, strikes a building 30 m
away at a point 15 above the ground. Find the velocity of projection.
Solution : As explained, the equation of projectile path suits the description of motion best.
Here,
x = 30 m, y = 15 m and θ = 45°. Now,

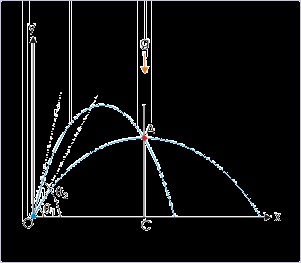

As pointed out earlier, we may need to determine the angle(s) for a given speed such that
projectile hits a specified target having known coordinates. This presents two possible angles with
which projectile can be thrown to hit the target. This aspect is clear from the figure shown here :
Figure 4.22. Projectile motion
Projectile motion
Clearly, we need to use appropriate form of equation of motion which yields two values of angle
of projection. This form is :
This equation, when simplified, form a quadratic equation in "tanθ". This in turn yields two values
of angle of projection. Smaller of the angles gives the projection for least time of flight.
Example 4.11.
Problem : A person standing 50 m from a vertical pole wants to hit the target kept on top of
the pole with a ball. If the height of the pole is 13 m and his projection speed is 10√g m/s,
then what should be the angle of projection of the ball so that it strikes the target in minimum
time?
Solution : Equation of projectile having square of “tan θ” is :






Putting values,
⇒ 25 tan2 θ – 100 tan θ + 51 = 0
Taking the smaller angle of projection to hit the target,
Determining attributes of projectile trajectory
A projectile trajectory under gravity is completely determined by the initial speed and the angle of
projection or simply by the initial velocity (direction is implied). For the given velocity,
maximum height and the range are unique – notably independent of the mass of the projectile.
Thus, a projectile motion involving attributes such as maximum height and range is better
addressed in terms of the equations obtained for the specific attributes of the projectile motion.
Example 4.12.
Problem : Determine the angle of projection for which maximum height is equal to the range
of the projectile.
Solution : We equate the expressions of maximum height and range (H = R) as :
Exercises
Exercise 15.
Which of the following is/ are independent of the angle of projection of a projectile :
(a) time of flight



(b) maximum height reached
(c) acceleration of projectile
(d) horizontal component of velocity
The time of flight is determined by considering vertical motion. It means that time of flight is
dependent on speed and the angle of projection.
Maximum height is also determined, considering vertical motion. As such, maximum height also
depends on the angle of projection.
Horizontal component, being component of velocity, depends on the angle of projection.
uy = u cos θ
It is only the acceleration of projectile, which is equal to acceleration due to gravity and is,
therefore, independent of the angle of projection. Hence, option (c) is correct.
Exercise 16.
Two particles are projected with same initial speeds at 30° and 60° with the horizontal. Then
(a) their maximum heights will be equal
(b) their ranges will be equal
(c) their time of flights will be equal
(d) their ranges will be different
The maximum heights, ranges and time of lights are compared, using respective formula as :
(i)Maximum Height




Thus, the maximum heights attained by two projectiles are unequal.
(ii) Range :
Thus, the ranges of two projectiles are equal.
(iii) Time of flight
Thus, the times of flight of two projectiles are unequal.
Hence, option (b) is correct.
Exercise 17.
The velocity of a projectile during its flight at an elevation of 8 m from the ground is 3 i - 5 j in
the coordinate system, where x and y directions represent horizontal and vertical directions
respectively. The maximum height attained (H) by the particle is :
We note that vertical component is negative, meaning that projectile is moving towards the
ground. The vertical component of velocity 8 m above the ground is
The vertical displacement (y) from the maximum height to the point 8 m above the ground as
shown in the figure can be obtained, using equation of motion.
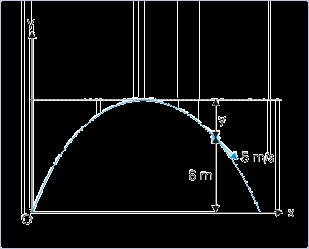





Figure 4.22. Projectile motion
Projectile motion
v 2 y = u 2 y + 2 a y
Considering the point under consideration as origin and upward direction as positive direction.
⇒ ( – 5 )2 = 0 + 2 X – 10 X h
Thus, the maximum height, H, attained by the projectile is :
Hence, option (c) is correct.
Exercise 18.
A projectile is thrown with a given speed so as to cover maximum range (R). If "H" be the
maximum height attained during the throw, then the range "R" is equal to :
The projectile covers maximum range when angle of projection is equal to 45°. The maximum
range "R" is given by :
On the other hand, the maximum height attained by the projectile for angle of projection, 45°, is :
Comparing expressions of range and maximum height, we have :







⇒ R = 4 H
Hence, option (a) is correct.
Exercise 19.
The speed of a projectile at maximum height is half its speed of projection, "u". The horizontal
range of the projectile is :
The horizontal range of the projectile is given as :
In order to evaluate this expression, we need to know the angle of projection. Now, the initial part
of the question says that the speed of a projectile at maximum height is half its speed of
projection, "u". However, we know that speed of the projectile at the maximum height is equal to
the horizontal component of projection velocity,
⇒ θ = 300
The required range is :
Hence, option (b) is correct.
Exercise 20.
Let " T 1 ” and “ T 2 ” be the times of flights of a projectile for projections at two complimentary
angles for which horizontal range is "R". The product of times of flight, " T 1 T 2 ”, is equal to : Here, we are required to find the product of times of flight. Let " θ " and " 900 − θ " be two angles of projections. The times of flight are given as :





































































