constant.
Angular velocity
The angular velocity increases by a constant value at the end of every unit time interval, when
angular velocity and acceleration act in the same direction. On the other hand, angular velocity
decreases, when angular velocity and acceleration act in the opposite direction.
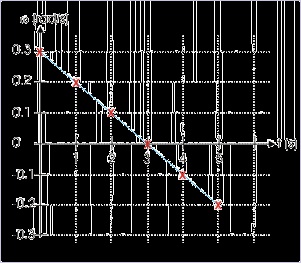
To appreciate this, we consider a circular motion of a particle whose initial angular velocity is 0.3
rad/s. The motion is subjected to an angular acceleration of magnitude 0.1
in the opposite
direction to the initial velocity. In the table here, we calculate angular velocity of the particle,
using relation, ω = ω 0 + α t , at the end of every second and plot the data (for first 5 seconds) to understand the variation of angular velocity with time.
-----------------------------------------------------
Time Angular acceleration Angular velocity
(s) (rad/s.s) (rad/s)
-----------------------------------------------------
0 -0.1 0.3
1 -0.1 0.3 - 0.1 x 1 = 0.2
2 -0.1 0.3 - 0.1 x 2 = 0.1
3 -0.1 0.3 - 0.1 x 3 = 0.0
4 -0.1 0.3 - 0.1 x 4 = -0.1
5 -0.1 0.3 - 0.1 x 5 = -0.2
-----------------------------------------------------
Here, the particle stops at the end of 3 seconds. The particle then reverses its direction (clockwise
from anti-clockwise) and continues to move around the axis. The angular velocity – time plot is as
shown here :
Figure 4.137. Angular velocity - time plot
We observe following aspects of the illustrated motion with constant acceleration :
1. The angular velocity decreases at uniform rate and the angular velocity – time plot is straight
line. Positive angular velocity becomes less positive and negative angular velocity becomes
more negative.
2. The slope of the plot is constant and negative.
Example 4.76.
Problem : A particle at the periphery of a disk at a radial distance 10 m from the axis of
rotation, uniformly accelerates for a period of 5 seconds. The speed of the particle in the
meantime increases from 5 m/s to 10 m/s. Find angular acceleration.
Solution : The initial and final angular velocities are :





Using equation of motion, ω = ω 0 + α t , we have :
Angular displacement
The angular displacement is given as :
If we start observation of motion as t = 0 and θ° = 0, then displacement (θ) is :
The particle covers greater angular displacement for every successive time interval, when angular
velocity and acceleration act in the same direction and the particle covers smaller angular
displacement, when angular velocity and acceleration act in the opposite direction.
To appreciate this, we reconsider the earlier case of a circular motion of a particle whose initial
angular velocity is 0.3 rad/s. The motion is subjected to an angular acceleration of magnitude 0.1
rad / s 2 in the opposite direction to the initial velocity. In the table here, we calculate angular
displacement of the particle, using relation,
, at the end of every second and plot the
data (for first 7 seconds) to understand the variation of angular displacement with time.
------------------------------------------------------------------------------------
Time wo t Angular displacement (θ)
(s) (rad) (rad)
------------------------------------------------------------------------------------
0 0.0 0.00
1 0.3 x 1 0.3 – 0.5 x 0.1 x 1 = 0.3 – 0.05 = 0.25
2 0.3 x 2 0.6 – 0.5 x 0.1 x 4 = 0.6 – 0.20 = 0.40
3 0.3 x 3 0.9 – 0.5 x 0.1 x 9 = 0.9 – 0.45 = 0.45
4 0.3 x 4 1.2 – 0.5 x 0.1 x 16 = 1.2 – 0.80 = 0.40
5 0.3 x 5 1.5 – 0.5 x 0.1 x 25 = 1.5 – 1.25 = 0.25
6 0.3 x 6 1.8 – 0.5 x 0.1 x 36 = 1.8 – 1.80 = 0.00
7 0.3 x 7 2.1 – 0.5 x 0.1 x 49 = 2.1 – 2.50 = -0.40
------------------------------------------------------------------------------------
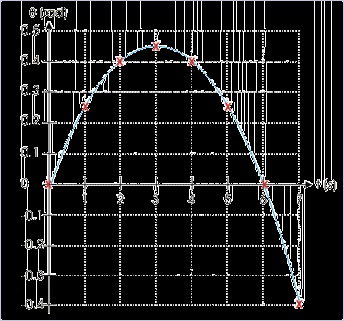




We see here that the particle moves in anti-clockwise direction for first 3 seconds as determined
earlier and then turns back (clockwise) retracing the path till it reaches the initial position.
Subsequently, the particle continues moving in the clockwise direction.
The angular displacement – time plot is as shown here :
Figure 4.138. Angular displacement – time plot
Example 4.77.
Problem : A particle at the periphery of a disk at a radial distance 10 m from the axis of
rotation, uniformly accelerates for a period of 20 seconds. The speed of the particle in the
meantime increases from 5 m/s to 20 m/s. Find the numbers of revolutions the particle
completes around the axis.
Solution : We need to find angular displacement to know the numbers of revolutions made.
Here,
To calculate angular displacement, we need to know angular acceleration. Here, we can
calculate angular acceleration as in the earlier exercise as :
Now, using equation of motion,
, we have :

The number of revolutions (nearest integer), n,
Exercises
Exercise 69.
The angular velocity .vs. time plot of the motion of a rotating disk is shown in the figure. Then,
Figure 4.138. Velocity .vs. time plot
Velocity .vs. time plot
angular acceleration is constant.
angular acceleration is negative.
disk comes to a stop at a particular instant.
disk reverses direction during the motion.
The slope of the straight line is a negative constant. Therefore, options (a) and (b) are correct. The
line crosses time axis, when angular velocity is zero. Thus option (c) is correct. The angular
velocities have opposite sign across time axis. It means that the disk reverses its direction. Thus
option (d) is correct.
Hence, options (a),(b),(c) and (d) are correct.
Exercise 70.
A point on a rotating disk, starting from rest, achieves an angular velocity of 40 rad/s at constant










A point on a rotating disk, starting from rest, achieves an angular velocity of 40 rad/s at constant
rate in 5 seconds. If the point is at a distance 0.1 meters from the center of the disk, then the
distance covered (in meters) during the motion is :
We can find the distance covered, if we know the angular displacement. On the other hand, we can
find angular displacement if we know the average angular speed as time is given.
We can consider this accelerated motion as uniform motion with average speed as calculated
above. The angular displacement is :
The distance covered is :
Exercise 71.
A point on a rotating disk completes two revolutions starting from rest and achieves an angular
velocity of 8 rad/s. If the angular velocity of the disk is increasing at a constant rate, the angular
acceleration ( rad / s 2 ) is :
We can use the equation of motion for constant acceleration. Here,
Looking at the data, it is easy to find that the following equation will serve the purpose,
Solving for "α" and putting values,



Hence, option (c) is correct.
Exercise 72.
A point on a rotating disk is accelerating at a constant rate 1 rad / s 2 till it achieves an angular
velocity of 10 rad/s. What is the angular displacement (radian) in last 2 seconds of the motion?
Here, final angular velocity, angular acceleration and time of motion are given. We can find the
angular displacement using equation of motion for angular displacement that involves final
angular velocity :
Putting values, we have :
Hence, option (a) is correct.
Circular motion with constant acceleration (application)*
Questions and their answers are presented here in the module text format as if it were an extension
of the treatment of the topic. The idea is to provide a verbose explanation, detailing the
application of theory. Solution presented is, therefore, treated as the part of the understanding
process – not merely a Q/A session. The emphasis is to enforce ideas and concepts, which can not
be completely absorbed unless they are put to real time situation.
Check understanding
An online examination, based on the basic subject matter, is available at the link given here. The
examination session is designed only for the basic level so that we can ensure that our
understanding of subject matter is satisfactory.
Circular motion with constant acceleration
Hints for problem solving
1: Visualize the circular motion as if we are dealing with straight line (pure translational) motion.

Write down formula with substitution of linear quantities with angular quantities.
2: Use formula in scalar form. Stick to anticlockwise measurement as positive and clockwise
measurement as negative.
Representative problems and their solutions
We discuss problems, which highlight certain aspects of the study leading to circular motion with
constant acceleration. The questions are categorized in terms of the characterizing features of the
subject matter :
Nature of angular motion
Time interval
Angular displacement
Nature of angular motion
Example 4.78.
Problem : The angular velocity .vs. time plot of the motion of a rotating disk is shown in the
figure.
Figure 4.139. angular displacement .vs. time plot
Determine (i) nature of angular velocity (ii) nature of angular acceleration and (iii) whether
the disk comes to a standstill during the motion?
Solution : The angular velocity is anticlockwise (positive) above time axis and clockwise
(negative) below time axis.




The slope of angular velocity - time plot indicates nature of acceleration. Since the plot is a
straight line, motion is accelerated/ decelerated at constant rate. Further, the slope of the
straight line (angular velocity - time plot) is negative all through out.
Recall that it is easy to determine the sign of the straight line. Just move from left to right in
the direction of increasing time along the time - axis. See whether the angular velocity
increases of decreases. If increases, then slope is positive; otherwise negative. The angular
velocity, here, becomes less positive above time axis and becomes more negative below time
axis. Hence, slope is negative all through out.
It means that acceleration (negative) is opposite to angular velocity (positive) above time axis.
Therefore, the disk is decelerated and the angular speed of disk decreases at constant rate.
Below time - axis, the angular acceleration is still negative. However, angular velocity is also
negative below the time axis. As such, disk is accelerated and the angular speed increases at
constant rate.
We see here that the plot intersects time - axis. It means that the disk comes to a stand still
before changing direction from anticlockwise rotation to clockwise rotation.
Time interval
Example 4.79.
Problem : The angular position of a point on a flywheel is given by the relation :
Find the time (in seconds) when flywheel comes to a stop.
Solution : The speed of the particle is :
When flywheel comes to a standstill, ω = 0,
Example 4.80.
Problem : The magnitude of deceleration of the motion of a point on a rotating disk is equal
to the acceleration due to gravity (10 m / s 2 ). The point is at a linear distance 10 m from the
center of the disk. If initial speed is 40 m/s in anti-clockwise direction, then find the time for
the point to return to its position.
Solution : The disk first rotates in anti-clockwise direction till its speed becomes zero and









then the disk turns back to move in clockwise direction. In order to analyze the motion, we
first convert linear quantities to angular quantities as :
When the point returns to its initial position, the total displacement is zero. Applying equation
of motion for angular displacement, we have :
⇒ t 2 − 8 t = 0
⇒ t ( t − 8 ) = 0
The zero time corresponds to initial position. The time of return to initial position, therefore,
is 8 seconds.
Angular displacement
Example 4.81.
Problem : A disk initially rotating at 80 rad/s is slowed down with a constant deceleration of
magnitude 4 rad / s 2 . What angle (rad) does the disk rotate before coming to rest ?
Solution : Initial and final angular velocities and angular acceleration are given. We can use
ω = ω 0 + α t to determine the time disk takes to come to stop. Here,
Using equation,
, we have :
Example 4.82.
Problem : The initial angular velocity of a point (in radian) on a rotating disk is 0.5 rad/s. The
disk is subjected to a constant acceleration of 0. 2 rad / s 2 . in the direction opposite to the
angular velocity. Determine the angle (in radian) through which the point moves in third
second.

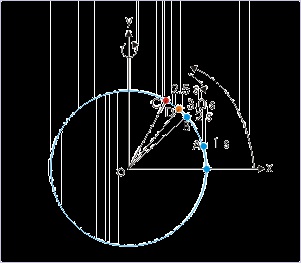



Solution : Here, we need to be careful as the point reverses its direction in the third second !
For ω = 0,
Thus the disk stops at t = 2.5 second. In this question, we are to find the angle (in rad) through
which the point moves in third second – not the displacement. The figure here qualitatively
depicts the situation. In the third second, the point moves from B to C and then from C to D.
The displacement in third second is BOD, whereas the angle moved in the third second is
|BOC| + |DOC|. Where,
∠BOC = displacement between 2 and 2.5 seconds.
∠DOC = displacement between 2.5 and 3 seconds.
Figure 4.140. Angle measurement
The angular velocity at the end of 2 seconds is :
The angular velocity at the end of 2.5 seconds is zero. Hence,
It means that the point, at t = 3 s, actually returns to the position where it was at t = 2 s. The
displacement is, thus, zero.
The total angle moved in third second = |0.025| + |-0.025| = 0.05 rad


Example 4.83.
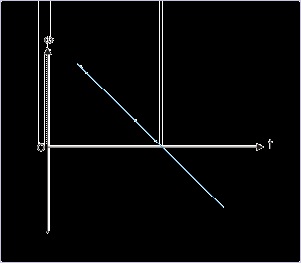
Problem : The angular velocity of a point (in radian) on a rotating disk is given by |t – 2|,
where “t” is in seconds. If the point aligns with the reference direction at time t = 0, then find
the quadrant in which the point falls after 5 seconds.
Problem : The area under the angular velocity – time plot and time axis is equal to angular
displacement. As required, let us generate angular velocity data for first 5 seconds to enable us
draw the requisite plot :
---------------------------------
Time (t) Angular velocity (θ)
(s) (rad/s)
---------------------------------
0 2
1 1
2 0
3 1
4 2
5 3
---------------------------------
The angular velocity – time plot is as shown in the figure :
Figure 4.141. Angular velocity – time plot
The displacement is equal to the area of two triangles :
Thus, the point moves 6.5 rad from the reference direction. Now, one revolution is equal to 2π
= 2 x 3.14 = 6.28 rad. The particle is, therefore, in the fourth quadrant with respect to the
reference direction.
Solutions
Index
Symbols
(i) , Combined input operations
(ii) , Combined input operations
(iii) , Combined input operations
., Products of vectors
1 :, Addition and subtraction to independent variable , Combined input operations
1. motion in two dimension : , Displacement and dimension of motion
1: , Attributes of scalar (dot) product , Attributes of vector (cross) product , Summary , Position
vector , External force and possible scenarios , Components of acceleration , Shortest path , Hints
on solving problems , Hints on solving problems , Coordinates along incline (x) and perpendicular
to incline (y) , Projection down the incline , Hints for solving problems , Tangential and normal
accelerations in circular motion , Nature of velocity and acceleration , Hints on problem solving ,
Circular motion with constant acceleration, Hints for problem solving
1: acceleration is zero , Velocity – time plot
2 :, Addition and subtraction to independent variable , Combined input operations
2. motion in one dimension : , Displacement and dimension of motion
2: , Attributes of scalar (dot) product , Attributes of vector (cross) product , Summary , Position
vector , External force and possible scenarios , Components of acceleration , Shortest path , Hints
on solving problems , Hints on solving problems , Coordinates along incline (x) and perpendicular
to incline (y) , Projection down the incline , Hints for solving problems , Tangential and normal
accelerations in circular motion , Nature of velocity and acceleration , Hints on problem solving ,
Circular motion with constant acceleration, Hints for problem solving
2: acceleration is constant , Velocity – time plot
3: , Attributes of scalar (dot) product , Attributes of vector (cross) product , Summary , Position
vector , External force and possible scenarios , Components of acceleration , Hints on solving
problems , Hints on solving problems , Coordinates along incline (x) and perpendicular to incline
(y) , Projection down the incline , Hints for solving problems , Nature of velocity and acceleration
, Hints on problem solving , Circular motion with constant acceleration
3: the magnitude of acceleration is increasing , Velocity – time plot
4: , Attr


















































