and
, where x denotes position and displacement as well. In the frame of reference with upward
direction as positive,
Putting these values in the equation, we have :
The important aspect of this equation is that it is a quadratic equation in time “t”. This equation
yields two values of time “t” for every position and displacement. This outcome is in complete
agreement with the actual motion as the ball reaches a given position twice (during upward and
downward motion). Only exception is point at the maximum height, which is reached only once.
We have seen earlier that ball reaches maximum height at t = 3 s. Therefore, maximum height,H,
is given as :
The displacement values for the motion at successive seconds are :
-------------------------------------------------------------
Time (t) ut 5txt Displacement
in seconds or position (x)
in meters
-------------------------------------------------------------
0.0 0 0 0
1.0 30 5 25
2.0 60 20 40
3.0 90 45 45
4.0 120 80 40
5.0 150 125 25
6.0 180 180 0
-------------------------------------------------------------
The corresponding displacement – time plot looks like as shown in the figure.



Figure 2.59. Displacement – time plot
We notice following important characteristics of the motion :
1: The ball retraces every position during motion except the point at maximum height.
2: The net displacement when ball return to initial position is zero. Thus, the total time of journey
(T) is obtained using displacement, x = 0,
Here, we neglect T = 0, which corresponds to initial position.
3: The “x” in equation
denotes displacement and not distance. Hence, it is not possible
to use this equation directly to obtain distance, when motion is not unidirectional.
Let us answer the question with respect to the motion of the ball under consideration : what is the
distance traveled in first 4 seconds? Obviously, the ball travels 30 m in the upward direction to
reach maximum height in 3 seconds and then it travels 5 m in the 4 th second in downward
direction. Hence, the total distance traveled is 45 + 5 = 50 m in 4 s. This means that we need to
apply the equation of motion in two parts : one for the upward motion and the second for the
downward motion. Thus, we find displacement for each segment of the motion and then we can
add their magnitude to obtain distance.
The distance values for the motion at successive seconds are :
------------------------------------------------------------
Time (t) ut 5t*t Displacement Distance
in seconds or position in meters
(x) in meters

------------------------------------------------------------
0.0 0 0 0 0
1.0 30 5 25 25
2.0 60 20 40 40
3.0 90 45 45 45
4.0 120 80 40 50
5.0 150 125 25 65
6.0 180 180 0 90
------------------------------------------------------------
Figure 2.60. Distance – time plot
Example 2.25. Constant acceleration
Problem : A balloon starts rising from the ground with an acceleration of 1.25 m/s. After 8
second, a stone is released from the balloon. Starting from the release of stone, find the
displacement and distance traveled by the stone on reaching the ground. Also, find the time
taken to reach the ground (take g = 10 m / s 2 ).
Solution : This question raises few important issues. First the rise of balloon is at a constant
acceleration of 1.25 m / s 2 . This acceleration is the “measured” acceleration, which is net of
the downward acceleration due to gravity. This means that the balloon rises with this net
vertical acceleration of 1.25 m / s 2 in the upward direction.
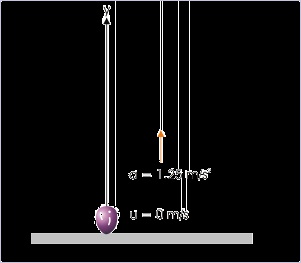


Figure 2.61. Motion under gravity
Here, u = 0; a = 1.25 m / s 2 ; t = 8 s. Let the balloon rises to a height “h” during this time,
then (considering origin on ground and upward direction as positive) the displacement of the
balloon after 8 seconds is :
Now, we know that, the body released from moving body acquires the velocity but not the
acceleration of the container body under motion. The velocity of the balloon at the instant of
separation is equal to the velocity of the balloon at that instant.
Thus, this is the initial velocity of the stone and is directed upward as that of the velocity of
balloon. Once released, the stone is acted upon by the force of gravity alone. The role of the
acceleration of the balloon is over. Now, the acceleration for the motion of stone is equal to
the acceleration due to gravity, g.
The path of motion of the stone is depicted in the figure. Stone rises due to its initial upward
velocity to a certain height above 40 m where it was released till its velocity is zero. From this
highest vertical point, the stone falls freely under gravity and hits the ground.
1: In order to describe motion of the stone once it is released, we realize that it would be
easier for us if we shift the origin to the point where stone is released. Considering origin at
the point of release and upward direction as positive as shown in the figure, the displacement
during the motion of stone is :
y = OB = - 40 m
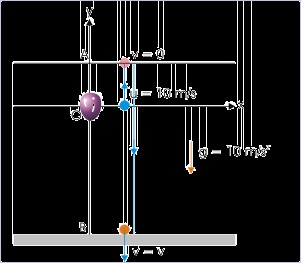



Figure 2.62. Motion under gravity
2: Distance, on the other hand, is equal to :
s = OA + AO + OB = 2 OA + OB
In order to obtain, OA, we consider this part of rectilinear motion (origin at the point of
release and upward direction as positive as shown in the figure).
Here, u = 10 m/s; a = -10 m / s 2 and v = 0. Applying equation of motion, we have :
Hence, OA = 5 m, and distance is :
s = 2 OA + OB = 2 x 5 + 40 = 50 m
3: The time of the journey of stone after its release from the balloon is obtained using
equation of motion (origin at the point of release and upward direction as positive as shown in
the figure).
Here, u = 12 m/s; a = -10 m / s 2 and y = - 40 m.
This is a quadratic equation in “t”. Its solution is :
As negative value of time is not acceptable, time to reach the ground is 4s.
It is important to realize that we are at liberty to switch origin or direction of reference
after making suitable change in the sign of attributes.



Position
We use the equation
normally in the context of displacement, even though the
equation is also designed to determine initial ( x 1 ) or final position ( x 2 ). In certain situations, however, using this equation to determine position rather than displacement provides more
elegant adaptability to the situation.
Let us consider a typical problem highlighting this aspect of the equation of motion.
Example 2.26.
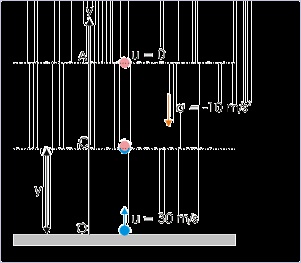
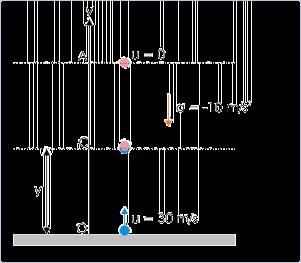
Problem : A ball is thrown vertically from the ground at a velocity 30 m/s, when another ball
is dropped along the same line, simultaneously from the top of tower 120 m in height. Find the
time (i) when the two balls meet and (ii) where do they meet.
Solution : This question puts the position as the central concept. In addition to equal time of
travel for each of the balls, rhe coordinate positions of the two balls are also same at the time
they meet. Let this position be “y”. Considering upward direction as the positive reference
direction, we have :
Figure 2.63. Vertical motion under gravity
The balls have same coordinate value when they meet.
For ball thrown from the ground :








()
For ball dropped from the top of the tower :
()
Now, deducting equation (2) from (1), we have :
Putting this value in equation – 1, we have :
One interesting aspect of this simultaneous motion of two balls is that the ball dropped from
the tower meets the ball thrown from the ground, when the ball thrown from the ground is
actually returning from after attaining the maximum height in 3 seconds. For maximum height
of the ball thrown from the ground,
Figure 2.64. Vertical motion under gravity
When returning from the maximum height, the ball thrown up from the ground is hit by the ball dropped from towers.
This means that this ball has actually traveled for 1 second (4 – 3 = 1 s) in the downward
direction, when it is hit by the ball dropped from the tower!
Exercises








Exercise 10.
A ball is thrown up in vertical direction with an initial speed of 40 m/s. Find acceleration of the
ball at the highest point.
The velocity of the ball at the highest point is zero. The only force on the ball is due to gravity.
The accleration of ball all through out its motion is acceleration due to gravity “g”, which is
directed downwards. The acceleration of the ball is constant and is not dependent on the state of
motion - whether it is moving or is stationary.
Exercise 11.
A ball is released from a height of 45 m. Find the magnitude of average velocity during its motion
till it reaches the ground.
The average velocity is ratio of displacement and time. Here, displacement is given. We need to
find the time of travel. For the motion of ball, we consider the point of release as origin and
upward direction as positive.
Neglecting negative time, t = 3 s. Magnitude of average velocity is :
Exercise 12.
A ball is released from an elevator moving upward with an acceleration
. What is the
acceleration of the ball after it is released from the elevator ?
On separation, ball acquires the velocity of elevator – not its acceleration. Once it is released, the
only force acting on it is that due to gravity. Hence, acceleration of the ball is same as that due to
gravity.
Exercise 13.
A ball is released from an elevator moving upward with an acceleration
. What is the
acceleration of the ball with respect to elevator after it is released from the elevator ?
On separation, ball acquires the velocity of elevator – not its acceleration. Once it is released, the










On separation, ball acquires the velocity of elevator – not its acceleration. Once it is released, the
only force acting on it is that due to gravity. Hence, acceleration of the ball is same as that due to
gravity. The relative acceleration of the ball (considering downward direction as positive) :
a rel = a ball – a elevator
Exercise 14.
A balloon ascends vertically with a constant speed for 5 second, when a pebble falls from it
reaching the ground in 5 s. Find the speed of balloon.
The velocity of balloon is constant and is a measured value. Let the ball moves up with a velocity
u. At the time of release, the pebble acquires velocity of balloon. For the motion of pebble, we
consider the point of release as origin and upward direction as positive. Here,
Using equation for displacement :
Exercise 15.
A balloon ascends vertically with a constant speed of 10 m/s. At a certain height, a pebble falls
from it reaching the ground in 5 s. Find the height of ballon when pebble is released from the
balloon.
The velocity of balloon is constant. Let the ball moves up with a velocity u. At the time of release,
the pebble acquires velocity of balloon. For the motion of pebble, we consider the point of release
as origin and upward direction as positive. Here,
Using equation for displacement :
⇒ y = 50 − 5 X 25
Height of ballon when pebble is released from it,







Exercise 16.
A ball is released from a top. Another ball is dropped from a point 15 m below the top, when the
first ball reaches a point 5 m below the top. Both balls reach the ground simultaneously.
Determine the height of the top.
We compare motion of two balls under gravity, when second ball is dropped. At that moment, two
balls are 10 m apart. The first ball moves with certain velocity, whereas first ball starts with zero
velocity.
Let us consider downward direction as positive. The velocity of the first ball when it reaches 10 m
below the top is :
v 2 = u 2 + 2 a x ⇒ v 2 = 0 + 2 X 10 X 5
Let the balls take time “t” to reach the gorund. First ball travels 10 m more than second ball. Let 1
and 2 denote first and second ball, then,
10 t = 10
In this time, second ball travels a distance given by :
But, second ball is 15 m below the top. Hence, height of the top is 15 + 5 = 20 m.
Exercise 17.
One ball is dropped from the top at a height 60 m, when another ball is projected up in the same
line of motion. Two balls hit each other 20 m below the top. Compare the speeds of the ball when
they strike.
For the motion of first ball dropped from the top, let downward direction be positive :
v 1 = u + a t ⇒ v 1 = a t = 10 t
For the ball dropped from the top,
⇒ 20 = 5 t 2
Neglecting negative value, t = 2s. Hence, velocity of the ball dropped from the top is :





For the motion of second ball projected from the bottom, let upward direction be positive :
v 2 = u + at ⇒ v 2 = u – 10 X 2 = u – 20
Clearly, we need to know u. For upward motion,
⇒ 40 = 2 u – 20 = 30 m / s
Thus,
See module titled “ Vertical motion under gravity (application) for more questions.
2.10. Vertical motion under gravity (application)*
Questions and their answers are presented here in the module text format as if it were an extension
of the treatment of the topic. The idea is to provide a verbose explanation, detailing the
application of theory. Solution presented is, therefore, treated as the part of the understanding
process – not merely a Q/A session. The emphasis is to enforce ideas and concepts, which can not
be completely absorbed unless they are put to real time situation.
Representative problems and their solutions
We discuss problems, which highlight certain aspects of the study leading to the accelerated
motion under gravity. The questions are categorized in terms of the characterizing features of the
subject matter :
Motion plots
Equal displacement
Equal time





Displacement in a particular second
Twice in a position
Collision in air
Motion plots
Example 2.27.
Problem : A ball is dropped from a height of 80 m. If the ball looses half its speed after each
strike with the horizontal floor, draw (i) speed – time and (ii) velocity – time plots for two
strikes with the floor. Consider vertical downward direction as positive and g = 10 m / s 2 .
Solution : In order to draw the plot, we need to know the values of speed and velocity against
time. However, the ball moves under gravity with a constant acceleration 10 m / s 2 . As such,
the speed and velocity between strikes are uniformly increasing or decreasing at constant rate.
It means that we need to know end values, when the ball strikes the floor or when it reaches
the maximum height.
In the beginning when the ball is released, the initial speed and velocity both are equal to zero.
Its velocity, at the time first strike, is obtained from the equation of motion as :
Corresponding speed is :
The time to reach the floor is :
According to question, the ball moves up with half the speed. Hence, its speed after first strike
is :
The corresponding upward velocity after first strike is :
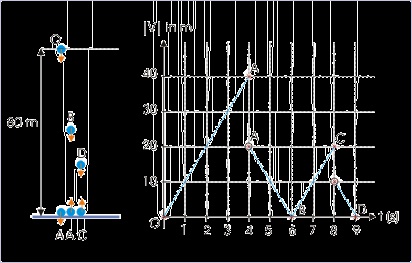
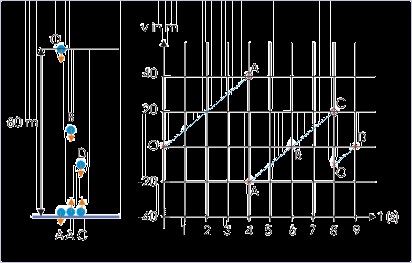




Figure 2.65. Speed – time plot
The ball dropped from a height looses half its height on each strike with the horizontal surface.
Figure 2.66. Velocity – time plot
The ball dropped from a height looses half its height on each strike with the horizontal surface.
It reaches a maximum height, when its speed and velocity both are equal to zero. The time to
reach maximum height is :
After reaching the maximum height, the ball returns towards floor and hits it with the same
speed with which it was projected up,
Corresponding speed is :
The time to reach the floor is :
Again, the ball moves up with half the speed with which ball strikes the floor. Hence, its speed
after second strike is :






The corresponding upward velocity after first strike is :
It reaches a maximum height, when its speed and velocity both are equal to zero. The time to
reach maximum height is :
Example 2.28.
Problem : A ball is dropped vertically from a height “h” above the ground. It hits the ground
and bounces up vertically to










































































