




The rate of change of velocity is equal to acceleration. For the given two dimensional motion,
2: The magnitude of rate of change of velocity
The magnitude of rate of change of velocity is equal to magnitude of acceleration. For the
given two dimensional motion,
3: The rate of change of speed
The rate of change of speed (dv/dt) is not equal to the magnitude of acceleration, which is
equal to the absolute value of the rate of change of velocity. It is so because speed is devoid of
direction, whereas acceleration consists of both magnitude and direction.
Let “v” be the instantaneous speed, which is given in terms of its component as :
We need to find rate of change of speed i.e dv/dt, using the values given in the question.
Therefore, we need to differentiate speed with respect to time,
If we ponder a bit, then we would realize that when we deal with component speed or
magnitude of component velocity then we are essentially dealing with unidirectional motion.
No change in direction is possible as components are aligned to a fixed axis. As such, equating
rate of change in speed with the magnitude of acceleration in component direction is valid.
Now, proceeding ahead,
Putting values, we have :
Note: This is an important question as it brings out differences in interpretation of familiar
terms. In order to emphasize the difference, we summarize the discussion as hereunder :
i: In general (i.e two or three dimensions),






ii: In the case of one dimensional motion, the inequality as above disappears.
Rectilinear motion with constant acceleration
Example 2.15.
Problem : A block is released from rest on a smooth inclined plane. If S n denotes the distance
traveled by it from t = n - 1 second to t = n seconds, then find the ratio :
Figure 2.40. Motion along an incline
The block moves with a constant acceleration.
Solution : It must be noted that the description of linear motion is governed by the equations
of motion whether particle moves on a horizontal surface (one dimensional description) or on
an inclined surface (two dimensional description). Let us orient our coordinates so that the
motion can be treated as one dimensional unidirectional motion. This allows us to use
equations of motion in scalar form,
Here, u = 0, thus
Following the description of term Sn as given by the question, we can define Sn+1 as the
linear distance from t = n second to t = n + 1 seconds. Thus, substituting “n” by “n+1” in the
formulae, we have :
The required ratio is :









Equations of motion
Example 2.16.
Problem : A force of 2 N is applied on a particle of mass 1 kg, which is moving with a
velocity 4 m/s in a perpendicular direction. If the force is applied all through the motion, then
find displacement and velocity after 2 seconds.
Solution : It is a two dimensional motion, but having a constant acceleration. Notably,
velocity and accelerations are not in the same direction. In order to find the displacement at
the end of 2 seconds, we shall use algebraic method. Let the direction of initial velocity and
acceleration be along “x” and “y” coordinates (they are perpendicular to each other). Also, let
“A” be the initial position and “B” be the final position of the particle. The displacement
between A (position at time t =0) and B (position at time t = 2 s) is given as :
For time t = 2 s,
This is a vector equation involving sum of two vectors at right angles. According to question,
Since u and a perpendicular to each other, the magnitude of the vector sum ( u + a) is :
Hence, magnitude of displacement is :
Let the displacement vector makes an angle “θ” with the direction of initial velocity.
Let the direction of initial velocity and acceleration be along “x” and “y” coordinates (they are
perpendicular to each other). Then,
Using equation of motion for constant acceleration, the final velocity is :
The magnitude of velocity is :






Let the final velocity vector makes an angle “θ” with the direction of initial velocity.
2.7. One dimensional motion with constant acceleration*
Free falling bodies under gravity represents typical case of motion in one dimension with constant
acceleration. A body projected vertically upwards is also a case of constant acceleration in one
dimension, but with the difference that body undergoes reversal of direction as well after reaching
the maximum height. Yet another set of examples of constant accelerations may include object
sliding on an incline plane, motion of an aboject impeded by rough surfaces and many other
motions under the influence of gravitational and frictional forces.
The defining differential equations of velocity and acceleration involve only one position variable
(say x). In the case of motion under constant acceleration, the differential equation defining
acceleration must evaluate to a constant value.
and
where k is a positive or negative constant.
The corresponding scalar form of the defining equations of velocity and acceleration for one
dimensional motion with constant acceleration are :
and
Example 2.17. Constant acceleration







Problem : The position “x” in meter of a particle moving in one dimension is described by the
equation :
where “t” is in second.
1. Find the time when velocity is zero.
2. Does the velocity changes its direction?
3. Locate position of the particle in the successive seconds for first 3 seconds.
4. Find the displacement of the particle in first three seconds.
5. Find the distance of the particle in first three seconds.
6. Find the displacement of the particle when the velocity becomes zero.
7. Determine, whether the particle is under constant or variable force.
Solution : Velocity is equal to the first differential of the position with respect to time, while
acceleration is equal to the second differential of the position with respect to time. The given
equation, however, expresses time, t, in terms of position, x. Hence, we need to obtain
expression of position as a function in time.
Squaring both sides, we have :
This is the desired expression to work upon. Now, taking first differential w.r.t time, we have :
1: When v = 0, we have v = 2t – 2 = 0
2. Velocity is expressed in terms of time as :
It is clear from the expression that velocity is negative for t < 1 second, while positive for t >
1. As such velocity changes its direction during motion.
3: Positions of the particle at successive seconds for first three seconds are :
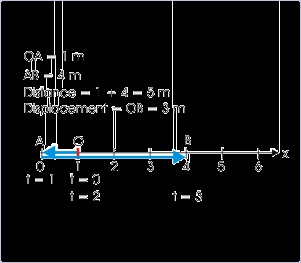


Figure 2.41. Graphical representation of position
4: Positions of the particle at t = 0 and t = 3 s are 1 m and 4 m from the origin.
Hence, displacement in first three seconds is 4 – 1 = 3 m
5: The particle moves from the start position, x = 1 m, in the negative direction for 1 second.
At t = 1, the particle comes to rest. For the time interval from 1 to 3 seconds, the particle
moves in the positive direction.
Distance in the interval t = 0 to 1 s is :
Total distance is 1 + 4 = 5 m.
6: Velocity is zero, when t = 1 s. In this period, displacement is 1 m.
7: In order to determine the nature of force on the particle, we first determine the acceleration
as :
Acceleration of the motion is constant, independent of time. Hence, force on the particle is
also constant during the motion.
Equation of motion for one dimensional motion with constant
acceleration
The equation of motions in one dimension for constant acceleration is obtained from the equations
of motion established for the general case i.e. for the three dimensional motion. In one dimension,
the equation of motion is simplified ( r is replaced by x or y or z with corresponding unit vector).
The three basic equations of motions are (say in x - direction) :





Significantly, we can treat vector equivalently as scalars with appropriate sign. Following is the
construct used for this purpose :
Sign convention
1. Assign an axis along the motion. Treat direction of axis as positive.
2. Assign the origin with the start of motion or start of observation. It is, however, a matter of
convenience and is not a requirement of the construct.
3. Use all quantities describing motion in the direction of axis as positive.
4. Use all quantities describing motion in the opposite direction of axis as negative.
Once, we follow the rules as above, we can treat equations of motion as scalar equations as :
Example 2.18. Constant acceleration
Problem : A car moving with constant acceleration covers two successive kilometers in 20 s
and 30 s respectively. Find the acceleration of the car.
Solution : Let "u" and "a" be the initial velocity and acceleration of the car. Applying third
equation of motion for first kilometer, we have :
At the end of second kilometer, total displacement is 2 kilometer (=2000 m) and total time is
20 + 30 = 50 s. Again applying third equation of motion,
Solving two equations,
Note that acceleration is negative to the positive direction (direction of velocity) and as such it
is termed “deceleration”. This interpretation is valid as we observe that the car covers second
kilometer in longer time that for the first kilometer, which means that the car has slowed
down.

It is important to emphasize here that mere negative value of acceleration does not mean it to
be deceleration. The deciding criterion for deceleration is that acceleration should be opposite
to the direction of velocity.
Motion under gravity
We have observed that when a feather and an iron ball are released from a height, they reach earth
surface with different velocity and at different times. These objects are under the action of
different forces like gravity, friction, wind and buoyancy force. In case forces other than gravity
are absent like in vacuum, the bodies are only acted by the gravitational pull towards earth. In
such situation, acceleration due to gravity, denoted by g, is the only acceleration.
The acceleration due to gravity near the earth surface is nearly constant and equal to 9.8 m / s 2 .
Value of ‘g’ is taken as 10 m / s 2 as an approximation to facilitate ease of calculation.
When only acceleration due to gravity is considered, neglecting other forces, each of the bodies
(feather and iron ball) starting from rest is accelerated at the same rate. Velocity of each bodies
increases by 9.8 m/s at the end of every second. As such, the feather and the iron ball reach the
surface at the same time and at the same velocity.
Additional equations of motion
A close scrutiny of three equations of motion derived so far reveals that they relate specific
quantities, which define the motion. There is possibility that we may encounter problems where
inputs are not provided in the manner required by equation of motion.
For example, a problem involvoing calaculation of displacement may identify initial velocity,
final velocity and acceleration as input. Now, the equation of motion for displacement is
expressed in terms of initial velocity, time and acceleration. Evidently, there is a mis-match
between what is given and what is required. We can, no doubt, find out time from the set of given
inputs, using equation for velocity and then we can solve equation for the displacement. But what
if we develop a relation-ship which relates the quantities as given in the input set! This would
certainly help.
From first equation :
From second equation :









Eliminating ‘t’,
()
This equation relates initial velocity, final velocity, acceleration and displacement.
Also, we observe that equation for displacement calculates displacement when initial velocity,
acceleration and time are given. If final velocity - instead of initial velocity - is given, then
displacement can be obtained with slight modification.
Using v = u + at,
()
Example 2.19. Constant acceleration in one dimensional motion
Problem : A train traveling on a straight track moves with a speed of 20 m/s. Brake is applied
uniformly such that its speed is reduced to 10 m/s, while covering a distance of 200 m. With
the same rate of deceleration, how far will the train go before coming to rest.
Solution : To know the distance before train stops, we need to know the deceleration. We can
find out deceleration from the first set of data. Here, u = 20 m/s ; v = 10 m/s ; x = 200 m ; a =
? An inspection of above data reveals that none of the first three equations of motion fits the
requirement in hand, while the additional form of equation v 2 – u 2 = 2 a x serves the purpose
:
For the train to stops, we have
and,






Displacement in a particular second
The displacement in a second is obtained by subtracting two displacements in successive seconds.
We calculate displacements in n th second and (n-1) th seconds. The difference of two
displacements is the displacement in the n th second. Now, the displacements at the end of n and
(n-1) seconds as measured from origin are given by :
The displacement in the n th second, therefore, is :
()
Example 2.20.
Problem : The equation of motion for displacement in n th second is given by :
This equation is dimensionally incompatible, yet correct. Explain.
Solution : Since “n” is a number, the dimension of the terms of the equation is indicated as :
Clearly, dimensions of the terms are not same and hence equation is apparently incompatible
in terms of dimensions.
In order to resolve this apparent incompatibility, we need to show that each term of right hand
side of the equation has dimension that of displacement i.e. length. Now, we know that the
relation is derived for a displacement for time equal to “1” second. As multiplication of “1” or
" 1 2 " with any term is not visible, the apparent discrepancy has appeared in otherwise correct
equation. We can, therefore, re-write the equation with explicit time as :
Now, the dimensions of the first and second terms on the right side are :






Thus, we see that the equation is implicitly correct in terms of dimensions.
Exercise 1.
If a particle, moving in straight line, covers distances “x”, “y” and “z” in p th , q th and r th seconds respectively, then prove that :
This is a motion with constant acceleration in one dimension. Let the particle moves with a
constant acceleration, “a”. Now, the distances in particular seconds as given in the question are :
Subtracting, second from first equation,
Similarly,
Adding three equations,
Average acceleration
Average acceleration is ratio of change in velocity and time. This is an useful concept where
acceleration is not constant throughout the motion. There may be motion, which has constant but
different values of acceleration in different segments of motion. Our job is to find an equivalent





constant acceleration, which may be used to determine attributes for the whole of motion. Clearly,
the single value equivalent acceleration should be such that it yields same value of displacement
and velocity for the entire motion. This is the underlying principle for determining equivalent or
average acceleration for the motion.
Example 2.21.
Problem : A particle starting with velocity “u” covers two equal distances in a straight line
with accelerations a 1 and a 2 . What is the equivalent acceleration for the complete motion?
Solution : The equivalent acceleration for the complete motion should yield same value for
the attributes of the motion at the end of the journey. For example, the final velocity at the end
of the journey with the equivalent acceleration should be same as the one calculated with
individual accelerations.
Here initial velocity is "u". The velocity at the end of half of the distance (say “x”) is :
Clearly, v 1 is the initial velocity for the second leg of motion,
Adding above two equations, we have :
This is the square of velocity at the end of journey. Now, let “a” be the equivalent
acceleration, then applying equation of motion for the whole distance (2x),
Comparing equations,
Interpretation of equations of motion
One dimensional motion felicitates simplified paradigm for interpreting equations of motion.
Description of motion in one dimension involves mostly the issue of “magnitude” and only one
aspect of direction. The only possible issue of direction here is that the body undergoing motion in
one dimension may reverse its direction during the course of motion. This means that the body
may either keep moving in the direction of initial velocity or may start moving in the opposite
direction of the initial velocity at certain point of time during the motion. This depends on the
relative direction of initial velocity and acceleration. Thus, there are two paradigms :
1. Constant force is applied in the direction of initial velocity.
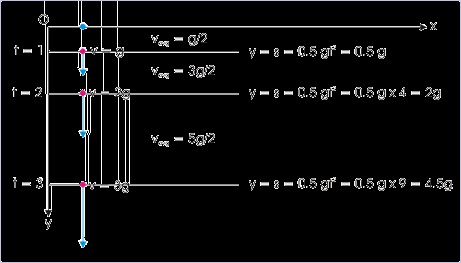


2. Constant force is applied in the opposite direction of initial velocity.
Irrespective of the above possibilities, one fundamental attribute of motion in one dimension is
that all parameters defining motion i.e initial velocity, final velocity and acceleration act along a
straight line.
<










































































