Space and Time by Laurentiu Mihaescu - HTML preview

3. Continuous or Discrete?

Is it necessary for a physical characteristic that is specific to the intrinsic nature of things, such as continuity, to be explicitly shown by its associated physical quantity? In other words, could we really say that a certain physical quantity is continuous or discrete? Or have we already assumed that and any unit of measure would be used, the numeric representation of a quantity is always limited and discrete, ignoring in this way the objective reality?

The presumption of a granular consistency for space, which is present in all my previous books and articles, has led me to a complete theory about the birth and evolution of our universe. All of the physical interactions, at any scale, are now explained by the simple rules of granular mechanics, while all the known laws of conservation have now real roots and became causally justified. But how can we characterize the true nature of the fundamental and derived physical quantities, whose measures quantify the interactions and give sense to the laws of physics, are they continuous or discrete? How can we define the border between the two possible assessments? And this border, if exists, is real or it is just a consequence of the observational and measurement limitations?

For example, let's take time: is it a continuous quantity or it must be quantized?

Current vision:

Time is a measurable physical quantity, and the second is its unit of measurement. Seen at first as a fraction of a day, the definition of the second has been improved later, being now the period in which a fixed number of oscillations produced by the cesium-133 atom takes place. There are a lot of multiples and submultiples for this accurate unit of measurement - from 10−24s (ys – yoctosecond) to 1024s (Ys – yottasecond). But how far can we go with these time intervals? As a mental exercise, would 10-100s make any sense, would it represent something? Intuitively, we should check at the quantum scale and see if, even at the speed of light, we can detect any motion. As this is practically impossible, a quantization at that small level could only be useful in some theoretical models. However, taking into account the dimensional scale of the elementary particles, we can set the minimum duration of time for an observable phenomenon. And does this minimum duration mean the maximum level of quantization possible for a seemingly continuous quantity? Or, at least theoretically, we should go even further, into the subquantum world?

Granular vision:

As a quantity that derives from motion, time must inherit this attribute from the source – i.e. from the motion of objects and particles. Thus, going down to the quantum scale, we could wonder if the motion of a particle is truly continuous, regardless of what the postulates of the Prime Theory [1] have stated. Considering the granular consistency of any particle and the constancy of the granular impulse, this is the only possible answer: the motion is continuous, all the intermediate positions on the respective trajectory are occupied.

What can we say about space, if it's seen as a geometric frame, as a scene? Is it a continuous and isotropic medium that does not interact with normal matter? The answer, this time, is not easy. If space is seen as a void, as a passive 3-dimensional frame in which matter can move freely, the answer is yes, space is a continuous medium. But this frame does not exist separately from the granular matter. Therefore, its uniformity and continuity are rather imposed by the granular component. Even if we are talking about a continuous frame, the granularity and all the other properties of the material component will affect all interactions between organized structures. The motion of any particle is continuous and free, but the intensity of its interactions is depending on the elementary impulse and energy [1]. Consequently, the physical quantities related to motion can be continuous, but those related to interactions are discrete up to the elementary quantities mentioned above, at least. As the order of magnitude involved is very small, this discretization is practically virtual and cannot be used in normal impulse and energy calculations.

Moreover, we must take into account the quantum uncertainty for all measurements (considering the Copenhagen interpretation of quantum mechanics). In addition to the observational uncertainty (Observer effect) – as a result of the interaction between the measuring device and a particular system, all quantum objects have an intrinsic uncertainty - as some pair of quantities cannot be quantified with high accuracy. For example, if the position of a particle could be determined with certain precision, its momentum cannot be measured with the same accuracy (Heisenberg's uncertainty principle). The granular consistency imposes to all particles, as Prime Theory [1] already described, a wavy behavior; therefore, some of the motion's pairs of attributes (energy/time, position/momentum) cannot be measured with the same precision (this also applies to quantum systems in general).

What if we, as special observers, would not interfere with the observed systems? In this case, the measurement of any physical quantity could be extremely accurate and, as there are no interactions, the wave functions would not collapse. In fact, the probability given by the wave function has no meaning now, we can determine all the states and variables of a quantum system. Our observations on the quantum realm would therefore help evaluate the continuity of any state parameter.

Quantum mechanics gives us certain limits (the Planck units) for some physical quantities (time, distance, etc.), setting a scale (the Planck scale) beyond which the current models of physics may no longer apply. Are these values representing a level that must be reached by discretization or the current theories of physics are not so coherent?

Table 7 contains all the physical constants used for the Planck units:

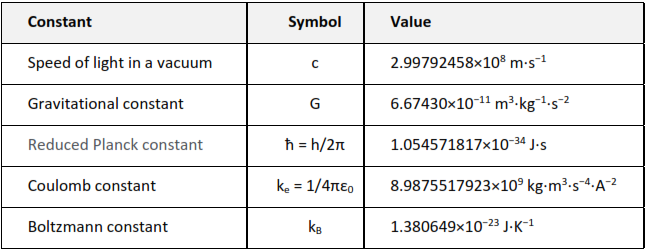
Table 7

Table 8

Table 8 shows the base Planck units; they resulted from a simple system of equations in which the physical constants are having the dimensionless value 1. In addition to the well-known uncertainty of some constants like G and ε0, there are other physical constants whose values remain to be analyzed. For example, the speed of light in a vacuum c - which, if seen beyond the inner relativism of our universe, cannot be considered a constant.

Moreover, this obvious inconsistency of the current theories of physics shall be added to their incompleteness. They do not take into consideration the granularity of space, nor its variable density (which is somehow compensated by the inner relativism of our universe, but which must be added to any model we would design).

Even if the Big Bang theory would be generally correct, it is clear now why there are no coherent explanations for the first moments of the universe (at least for the Planck interval)! In addition, the causality, the energy/mass, the laws of physics are all practically compromised in this theory! As this theory of the early universe breaks since the beginning, a rational solution has already been formulated: my distributed model called the First Bang [2], which explains how space became a granular medium and how it expands.

In fact, these Planck units must be regarded with reservation. They do neither determine the level of discretization for those physical quantities nor establish a physical limit beyond which we cannot pass. They only tell us that the current models and equations are not designed to work at the Planck scale. For example, the Planck length has nothing to do with the granularity of space, and we should never mix up these two similar values! Moreover, these Planck units do not validate a so- called invariant scaling of nature, as they are not based on some absolute constants!

Prime Theory series has introduced a set of absolute physical quantities that may justify the attribute discrete for their derived quantities (Table 9). If we would express these elementary quantities by using the standard units of measurement, their values would be too large or too small and we could not work normally with them. Anyway, they all are discrete quantities and this thing should be said once again. Moreover, a scalar or vectorial combination of these elementary quantities (more or less useful at granular level) is also discrete and this cannot change any law of physics! These things were only mentioned to better understand the connection between the granular model and the standard model of quantum physics.

Table 9

As ideal observers, we could easily find out if a certain physical quantity must bear the attribute of continuous or not, and this might help us decipher all the mechanisms of nature. As real observers, though, we are forced to work with uncertain values - that can be considered discrete anyway - when the quantum realm is involved.