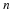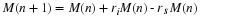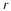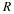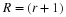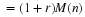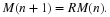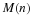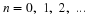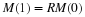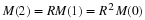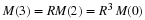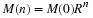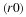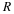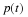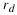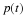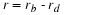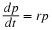If a system is modeled by a differential equation, and if the equations are numerically solved on a digital computer or calculator, the system is said to be simulated on the computer. If the model is valid and the numerical methods accurate, experiments can be performed on the computer simulation that might be impossible to conduct otherwise.
Consider several examples that use the models already discussed. If a population is governed by a linear first-order equation
one would not be able to "solve" this equation on a computer. If, however, we use Euler's method as was done in (14) by approximating the derivative as
where time is considered at intervals of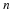 
,
This gives for (1) .EQ (34)
If we include the time interval T in the functional notation by
then (3) becomes
which is now in a form that one can easily calculate successive values of x(n) given any initial value. This can be programmed on a computer or simply done on a hand calculator.
Next, consider the nonlinear equation that models a population with a simple limit given by (23).
Using Euler's method again gives
This equation is complex enough to illustrate several points;
therefore, we will examine several numerical solutions.
Equation 6.8 was programmed on a Tektronix 31 programmable calculator
with a plotter automatically plotting the solutions by drawing straight
lines between successive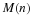 
.
First, consider a low-density growth rate
of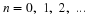 
or 10% per year for an initial population
of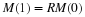 
over a time period of 100 years.
We will use for the reducing effect on the growth rate in (2), a value
of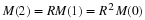 
, which implies a carrying capacity for the
system of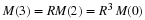 
.
For the Euler method, a time interval of 
years is used,
which means 50 calculations of (6) will be necessary for the 100-year
period.
The curves in Figure A are the output of the simulation for the above parameters and also for other growth rates of 5% and 20%. Note the solution always approaching the same limit but requiring different amounts of time.
In Figure B, the model is run assuming several different initial
populations.
Again, the solutions always approach the limit of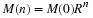 
, even if the
initial population is greater than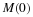 
.
Figure C shows the effects of various amounts of limiting by
considering various values for the factor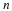 
, and
therefore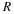 
, the carrying capacity.
When the limit is removed (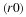
), the growth is exponential.
These examples illustrate the kinds of questions that can be pursued
by running experiments on the computer simulation.
There is one more point that should be considered.
It has nothing to do with the differential equation model (23) but with
the numerical procedure, Euler's method.
Consider the effects of using various time intervals T while holding everything else constant.
Figure D shows the results of this experiment.
The curve resulting from using a time interval
of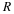 
years looks essentially the same as the exact solution
of the differential equation.
The numerical solution deviates more as T is increased until,
for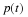 
years, it has lost the character of the exact solution.
A method for checking to see if T is sufficiently small is to try
halving it until the change is small.
One last point should be made concerning this numerical simulation. Euler's method is the only approach to numerically solve (23) that has been discussed. That is not because it is the best – there are far more efficient and sophisticated methods – but that is not our subject here, so we will continue with the straightforward algorithm of Euler.
The super-exponential logistic equation of (31) was simulated on the
calculator and run with a low population growth rate
of 
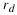, a
maximum rate of 
, and a carrying capacity
of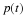 
.
This solution is shown in Figure E and compared with an exponential
of the same 
, and a simple logistic of the
same ro and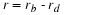 
.
The model was run again with a maximum growth rate of 
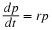, and
the results are shown in Figure F.
Note the initial exponential growth which becomes super-exponential,
growing extremely rapidly, then abruptly leveling off to an
equilibrium.