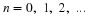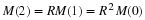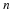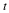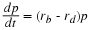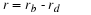In this module we will present several
definitions and a language that will later be used to model social
systems. Although a complete and detailed presentation will not be
made, the ideas covered are very important for anything other than
a superficial understanding of dynamic models. Much of this
material grew out of what is called system theory and control
theory. 12
As we noted before, it is sometimes difficult
to give clear, precise definitions of some ideas. That is the case
for the definition of a system which sounds a bit vague but seems
to be as good as possible.
A system is defined as a set of interrelated
entities, variables, or ideas that have some common features or
purpose.
Examples of systems would be a car, a radio,
a transportation network, a set of coupled equations, a society, a
family, etc. The system may be physical, biological, social,
conceptual, or many other forms.
The dynamics of a system is the way the
various variables of the system change and evolve with
time.
The study of dynamics is an important part of
physics, engineering, and economics. Indeed, the study of change in
history, psychology, etc. can be viewed as a study of dynamics, and
when anyone makes predictions about the future, he is certainly
using a dynamic model whether he realizes it or not. There are many
studies of systems which are not dynamic models - these use static
or equilibrium models and study relationships where time variations
are assumed not important. The mathematics often used in the study
of system dynamics are calculus and differential equations.
The structure of a system is the
specification of the components of importance and interest and the
description of the relations and interconnections within the
system.
The choice of structures may be easy or very
difficult depending on the system. In many physical systems the
structure is fairly well developed, however, for social systems it
is more complicated. The choice of age groupings, economic
groupings, etc. by a sociologist is the choice of structure for a
particular system. Indeed, much of the research in the social
sciences has centered around structure with relatively little work
being done explicitly on dynamics. For our purposes, we need
both.
There are two rather different but
complimentary descriptions that have been used with success in
systems analysis. One is an input-output or external approach, and
the other is a state variable or interval approach. Both have
merits and will be briefly described.
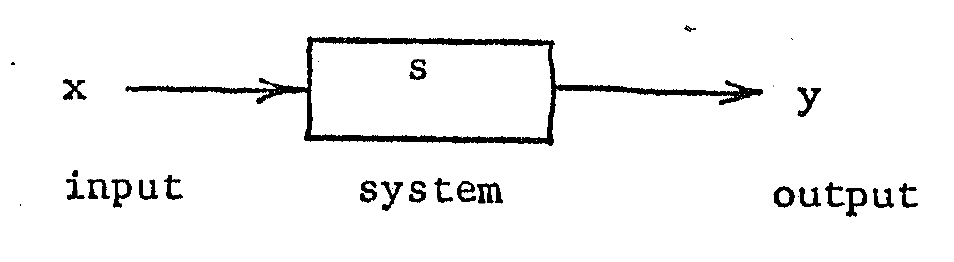
The Input-Output Description
Here there are three entities considered: the
input x , output y , and the system s . Symbolically, this is
illustrated by
This has proven a very valuable approach that
avoids internal details of the system that are of no interest or
are difficult to describe.
There are three problems that can be formulated
with this description:
Analysis: x and s given, find y ;
Synthesis: x and y given, find s ; and
Control: s and y given, find x .
In the modeling of systems and signals, one
often has a partial description of all three, and they must be
completed in a way to be consistent.
The State Variable or Internal
In this case, a detailed description of the
internal structure of a model is made. The idea of a "state" is
very important to dynamic systems, but is so fundamental as to be
difficult to define. The situation if further complicated by the
fact that the word state is used in many different ways in other
areas.
The state of system is the present
information about the past that allows one of predict the effect of
the past on the future. The variables that describe the state are
called the state variables and the minimum number of state
variables is called the order (or dimension) of the system.
For example, if one is modeling a social
system, in order to predict the future population, in addition to
other factors, one must know the present population; therefore,
population would be a state variable. Another example might be a
second-order differential equation.
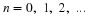
Here x(o) and 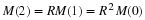 are needed to calculate
x(t) ; therefore, they could be stat & variables. A mechanical
example would be a moving mass where one would have to know the
position x and velocity v at some time to predict its future
position.
are needed to calculate
x(t) ; therefore, they could be stat & variables. A mechanical
example would be a moving mass where one would have to know the
position x and velocity v at some time to predict its future
position.
In addition to state variables, a system
often has many variables that are derived from present values of
other variables, but do not require any past values. These are very
important in the description of some systems, and it is often very
difficult to distinguish between state and derived variables when
initially trying to set up a model for a complex system.
The difficulty in choosing state variables is
further compounded by the fact that they are not unique. (Their
number is, however.) For example, in a system of equations, a
change of variables could be carried out and the new variables used as states. In the mechanical example, one could choose
v
+
x
for
one state variable and
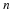 for the other, although it's hard to
imagine why one would want to.
for the other, although it's hard to
imagine why one would want to.
Deterministic and Probabilistic
Still another division of description is into
those that use deterministic equations to relate the various system
variables and those that relate the statistics of the variables.
These two approaches are complimentary. For example, in describing
a gas in a container, one can relate the gross characteristics of
pressure, temperature and volume by an algebraic equation; however,
one must resort to statistics to describe an individual molecule.
In the case of the social model, it seems to also hold that
individual people or small groups must be described statistically,
but the gross behavior of large aggregates can be described
deterministically. This is certainly not as clear-cut as for a
container of gas, but it is what we will follow.
Indeed, not only is the decision between a
deterministic and probabilistic model difficult to make for a
social system, but the choice of structure, state variables, and
many other factors are all difficult and the subject of much debate
a long researchers. What this means, however, is the basic concepts
and definitions must be understood even better and used with even
greater care.
There are a number of rather common
classifications of systems that prove useful. The two most
important are given here in terms of an input-output
description.
| A. A system is called linear if, and only if,
the following two conditions hold. In an input
x1 causes an output
y1, and an input
x2 causes an output
y2, then an input which is
the sum of two inputs,
x1
+
x2 , must cause an output
y1
+
y2.
This is called superposition. If the input
x1 is scaled by an
arbitrary value a , then the resulting output must also be scaled
by the same value
a . |
(3.1)
F
=
M
⋅
A
| B. A system is called time-invariant or
stationary if, and only if, the following is true for arbitrary t
. |
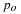 .
.
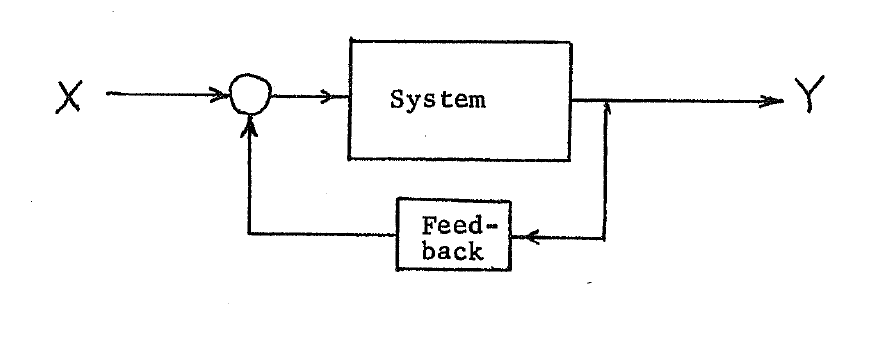
A particular structure [Luenberger 1979] which
is so important that it warrants special discussion has the feature
that the output affects the input. This is illustrated by the
following figure.
Feedback is often part of naturally occurring
systems and it also is often a part of constructed systems. The
most common feedback system is probably the thermostat that uses a
measured temperature to feedback a controlling signal to a heater
in an oven or room heating system. The filling mechanism in the
tank of a toilet uses a float to feedback a measure of the water
level to control the input valve. A person's blood sugar level is
controlled by a complicated biological feedback system. The power
steering of a car, the auto-pilot of an airplane, and the control
of a satellite rocket are all examples of feedback.
An interesting model using feedback can be
used to describe a bank savings account. Here the output can be the
amount of interest earned which is then fed back and added to
increase the account. This feedback is called compounding, and
results in the rapid exponential growth of an account.
A similar model will be used to describe a
population where the feedback signal is the number of people added
by births less the number of deaths. This forms the basis of the
exponential predictions of population growth, and we will explore
it in detail later.
The basis of the free marketplace is based on
feedback through price changes to cause the supply to follow the
demand.
While feedback is a useful concept, its
effects become more difficult to predict as the systems become more
complex. A simple example illustrates one problem. Consider a
person adjusting the temperature of his shower by the hot and cold
valves. If there is a time delay introduced by a length of pipe
between the valves and the shower head, the person will over
control. If the water is initially too hot, he will turn on the
cold water, but because of the delay, no effect is immediately felt
so more cold water is turned on. This continues until finally the
now very cold water reaches the shower head, whereupon the person
starts the same procedure of increasing the hot water. This
oscillation will continue until the person "gets smart" and allows
for the delay. A similar problem can occur in college education
because of the four-year delay between the choice of a major and
the graduation to a job.
A bit of reflection begins to show the
complicated nature of a social system will involve multi-variable
nonlinear systems with time delays and multiple feedback
loops.