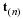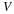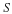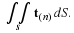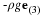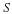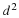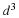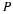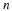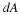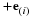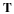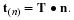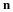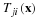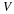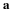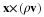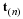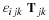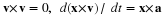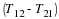We will now substitute the constitutive equation for a Newtonian fluid into Cauchy's equation of motion to derive the Navier-Stokes equation.

Cauchy's equation of motion is

(6.1)

The constitutive equation for a Newtonian fluid is

(6.2)

The divergence of the rate of deformation tensor needs to be restated with a more meaningful expression.

(6.3)

Thus

(6.4)

Substituting this expression into Cauchy's equation gives the Navier-Stokes equation.

(6.5)

The Navier-Stokes equation is sometimes expressed in terms of the acceleration by dividing the equation by the density.

(6.6)

where v=μ/ρ and λ^'=λ/ρ . ν is known as the kinematic viscosity and if Stokes' relation is assumed λ^'+ν=ν/3. Using the identities

(6.7)

the last equation can be modified to give

(6.8)

If the body force f can be expressed as the gradient of a potential (conservative body force) and density is a single valued function of pressure (piezotropic), the Navier-Stokes equation can be expressed as follows.

(6.9)

Do exercises 6.11.1, 6.11.2, 6.11.3, and 6.11.4 in Aris.

Later we will discuss the dimensionless groups resulting from the differential equations and boundary conditions. However, it is instructive to derive the Reynolds number N_Re from the Navier-Stokes equation at this point. The Reynolds number is the characteristic ratio of the inertial and viscous forces. When it is very large the inertial terms dominate the viscous terms and vice versa when it is very small. Its value gives the justification for assumptions of the limiting cases of inviscid flow and creeping flow.

We will consider the case of single-phase flow with conservative body forces (e.g., gravitational) and density a single valued function of pressure. The pressure and potential from the body force can be combined into a single potential.

(6.10)

If the change in density is small enough, the potential can be approximated by potential that has the units of pressure.

(6.11)

Suppose that the flow is characterized by a certain linear dimension, L, a velocity U, and a density ρ . For example, if we consider the steady flow past an obstacle, L may be it's diameter and U and ρ the velocity and density far from the obstacle. We can make the variables dimensionless with the following

(6.12)

The conservative body force, Navier-Stokes equation is made dimensionless with these variables.

(6.13)

The Reynolds number partitions the Navier -Stokes equation into two parts. The left side or inertial and potential terms, which dominates for large NRe and the right side or viscous terms, which dominates for small NRe. The potential gradient term could have been on the right side if the dimensionless pressure was defined differently, i.e., normalized with respect to (μU)/L, the shear stress rather than kinetic energy. Note that the left side has only first derivatives of the spatial variables while the right side has second derivatives. We will see later that the left side may dominate for flow far from solid objects but the right side becomes important in the vicinity of solid surfaces.

The nature of the flow field can also be seen form the definition of the Reynolds number. The second expression is the ratio of the characteristic kinetic energy and the shear stress.

The alternate form of the dimensionless Navier-Stokes equation with the other definition of dimensionless pressure is as follows.

(6.14)

If there was no dissipation of mechanical energy during fluid motion then kinetic energy and potential energy can be exchanged but the change in the sum of kinetic and potential energy would be equal to the work done to the system. However, viscous effects result in irreversible conversion of mechanical energy to internal energy or heat. This is known as viscous dissipation of energy. We will identify the components of mechanical energy in a flowing system before embarking on a total energy balance.

The rate that work W is done on fluid in a material volume V with a surface S is the integral of the product of velocity and the force at the surface.

(6.15)

The last integrand is rather complicated and is better treated with index notation.

(6.16)

We made use of Cauchy's equation of motion to substitute for the divergence of the stress tensor. The integrals can be rearranged as follows.

(6.17)

The left-hand term can be identified to be the rate of change of kinetic energy. The first term on the right-hand side is the rate of change of potential energy due to body forces. The second term is the rate at which surface stresses do work on the material volume. We will now focus attention on the last term.

The last term is the double contracted product of the stress tensor with the velocity gradient tensor. Recall that the stress tensor is symmetric for a nonpolar fluid and the velocity gradient tensor can be split into symmetric and antisymmetric parts. The double contract product of a symmetric tensor with an antisymmetric tensor is zero. Thus the last term can be expressed as a double contracted product of the stress tensor with the rate of deformation tensor. We will use the expression for the stress of a Newtonian fluid.

(6.18)

where Φ is the second invariant of the rate of deformation tensor. Thus the rate at which kinetic energy per unit volume changes due to the internal stresses is divided into two parts:

Since Θ²–2Φ is always positive, this last term is always dissipative. If Stokes' relation is used this term is

(6.20)

for incompressible flow it is

(The above equation is sometimes written –4μΦ, where Φ is called the dissipation function. We have reserved the symbol Φ for the second invariant of the rate of deformation tensor, which however is proportional to the dissipation function for incompressible flow. Y is the symbol used later for the negative of the dissipation by viscous forces.)

We need the formulation of the energy equation since up to this point we have more unknowns than equations. In fact we have one continuity equation (involving the density and three velocity components), three equations of motion (involving in addition the pressure and another thermodynamic variable, say the temperature) giving four equations in six unknowns. We also have an equation of state, which in incompressible flow asserts that ρ is a constant reducing the number of unknowns to five. In the compressible case it is a relation

which increases the number of equations to five. In either case, there remains a gap of one equation, which is filled by the energy equation.

The equations of continuity and motion were derived respectively from the principles of conservation of mass and momentum. We now assert the first law of thermodynamics in the form that the increase in total energy (we shall consider only kinetic and internal energies) in a material volume is the sum of the heat transferred and work done on the volume. Let q denote the heat flux vector, then, since n is the outward normal to the surface, –q•n is the heat flux into the volume. Let U denote the specific internal energy, then the balance expressed by the first law of thermodynamics is

(6.23)

This may be simplified by subtracting from it the expression we already have for the rate of change of kinetic energy, using Reynolds transport theorem, and Green's theorem.

(6.24)

Since this is valid for any arbitrary material volume, we have assumed continuity of the integrand

(6.25)

We assume Fourier's law for the conduction of heat.

We assume a Newtonian fluid for the dissipation of energy.

(6.27)

Substituting this back into the energy balance we have

(6.28)

Physically we see that the internal energy increases with the influx of heat, the compression and the viscous dissipation.

If we write the equation in the form

(6.29)

the left-hand side can be transformed by one of the fundamental thermodynamic identities. For if S is the specific entropy,

(6.30)

Substituting this into the last equation for internal energy gives

(6.31)

Giving an equation for the rate of change of entropy. Dividing by T and integrating over a material volume gives

(6.32)

The second law of thermodynamics requires that the rate of increase of entropy should be no less than the flux of heat divided by temperature. The above equation is consistent with this requirement because the volume integral on the right-hand side cannot be negative. It is zero only if k or ∇T and are zero. This equation also shows that entropy is conserved during flow if the thermal conductivity and viscosity are zero.

(6.33)

Do exercises 6.3.1 and 6.3.2 in Aris.

Isentropic flow. The condition of zero viscosity and thermal conductivity results in conservation of entropy during flow or isentropic flow. This ideal condition is useful for illustration the effect of compressibility on fluid dynamics. The conservation of entropy during flow implies that density, pressure, and temperature are changing in a reversible manner during flow. The relation between entropy, density, temperature, and pressure is given by thermodynamics.

(6.34)

These relations may be combined with the condition that the material derivative of entropy is zero to obtain a relation between temperature and pressure during flow.

(6.35)

The equation of state expresses the density as a function of temperature and pressure. During isentropic flow the pressure and temperature are not independent but are constrained by constant entropy or adiabatic compression and expansion. The density in this case is given as

We now have as many equations as unknowns and the system can be determined. The simplifying feature of isentropic flow is that exchanges between the internal energy and other forms of energy are reversible, and internal energy and temperature play passive roles, merely changing in response to the compression of a material element. The continuity equation and equation of motion governing isotropic flow may now be expressed as follows.

(6.37)

The physical significance of the parameter c, which has the dimensions of velocity, may be seen in the following way. Suppose that a mass of fluid of uniform density ρ_o is initially at rest, in equilibrium, so that the pressure p_o is given by

The fluid is then disturbed slightly (all changes being isentropic), by some material being compressed and their density changed by small amounts, and is subsequently allowed to return freely to equilibrium and to oscillate about it. (The fluid is elastic, and so no energy is dissipated, so oscillations about the equilibrium are to be expected.) The perturbation quantities 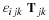and 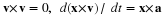and v are all small in magnitude and a consistent approximation to the continuity equation and equations of motion is

(6.39)

where c_o is the value of c at ρ=ρ_o . On eliminating v we have

(6.40)

Page 1Page 2Page 3Page 4Page 5Page 6Page 7Page 8Page 9Page 10Page 11Page 12Page 13Page 14Page 15Page 16Page 17Page 18

PREV   NEXT