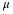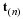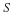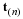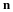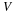Prerequisites and text books
Students in this class are expected to have a background corresponding to a BS degree in Chemical Engineering. This includes a course in multivariable calculus, which covers the algebra and calculus of vectors fields on volumes, surfaces, and curves of 3-D space and time. Courses in ordinary and partial differential equations are a prerequisite. Some elementary understanding of fluid mechanics is expected from a course in transport phenomena, fluid mechanics, or physics. It is assumed that not all students have the prerequisite background. Thus, material such as vector algebra and calculus will be briefly reviewed and exercise problems assigned that will require more reading from the student if they are not already familiar with the material.
The two required textbooks for this course are R. Aris, Vectors, Tensors, andthe Basic Equations of Fluid Mechanics and Bird, Stewart, and Lightfoot, Transport Phenomena. Several of the classical problems are from S. W. Churchill, Viscous Flows, The Practical Use of Theory. The classical textbook, Feyman, Leighton, and Sands, The Feyman Lectures on Physics, Volume II is highly recommended for its clarity of presentation of vector fields and physical phenomena. The students are expected to be competent in MATLAB, FORTRAN, and EXCEL and have access to Numerical Recipes in FORTRAN.
The following table is a suggested book list for independent studies in transport phenomena.
Table 1.1. Transport phenomena book list| Author | Title | Publisher | Year |
|---|
| L.D. Landau andE. M. Lifshitz | Fluid Mechanics, 2nd Ed. | Butterworth | 1987 |
| V. G. Levich | Physicochemical Hydrodynamics | Prentice-Hall | 1962 |
| S. Chandrasekhar | Hydrodynamics and Hydromagnetic Stability | Dover | 1961 |
| H. Schlichting | Boundary Layer Theory | McGraw-Hill | 1960 |
| H. Lamb | Hydrodynamics | Dover | 1932 |
| S. Goldstein | Modern Developments in Fluid Dynamics | Dover | 1965 |
| W. E. Langlois | Slow Viscous Flow | Macmillan | 1964 |
| J. Happel, H. Brenner | Low Reynolds Number Hydrodynamics | Kluwer | 1973 |
| G. K. Batchelor | An Introduction to Fluid Mechanics | Cambridge | 1967 |
| S.-I. Pai | Viscous Flow Theory I Laminar Flow | Van Nostrand | 1956 |
| M. Van Dyke | Perturbation Methods in Fluid Mechanics | Academic Press | 1964 |
| S. W. Churchill | Inertial Flows | Etaner | 1980 |
| S. W. Churchill | Viscous Flows | Butterworths | 1988 |
| R. F. Probstein | Physicochemical Hydrodynamics | Butterworth-Heinemann | 1989 |
| S. Middleman | An Introduction to Fluid Dynamics | John Wiley | 1998 |
| S. Middleman | An Introduction to Mass and Heat Transfer | John Wiley | 1998 |
| E. L. Koschmeider | Benard Cells and Taylor Vortices | Cambridge | 1993 |
| W.-J. Yang | Handbook of Flow Visualization | Taylor & Francis | 1989 |
| W.-J. Yang | Computer-Assisted Flow Visualization | CRC Press | 1994 |
| A. J. Chorin | Computational Fluid Mechanics | Academic Press | 1989 |
| A. J. Chorin, J. E. Marsden | A Mathematical Introduction to Fluid Mechanics | Springer-Verlag | 1993 |
| L. C. Wrobel,C. A. Brebbia | Computational Modeling of Free and Moving Boundary Problems, Vol. 1 Fluid Flow | Computational Mechanics Publications | 1991 |
| M. J. Baines,K. W. Morton | Numerical Methods for Fluid Dynamics | Oxford | 1993 |
| W. E. Schiesser,C. A. Silebi | Computational Transport Phenomena | Cambridge | 1997 |
| N. Ida, J. P. A. Bastos | Electro-Magnetics and Calculation of Fields | Springer | 1997 |
| L. G. Leal | Laminar Flow and Convective Transport Processes | Butterworth | 1992 |
| W. M. Deen | Analysis of Transport Phenomena | Oxford | 1998 |
| C. S. Jog | Foundations and Applications of Mechanics, Vol. I, Continuum Mechanics | CRC Press | 2002 |
| C. S. Jog | Foundations and Applications of Mechanics, Vol. II, Fluid Mechanics | CRC Press | 2002 |
| T.J. Chung | Computational Fluid Dynamics | Cambridge | 2002 |
| R. J. Kee, M.E. Coltrin, P. Glarborg | Chemically Reacting Flow | Wiley - Interscience | 2003 |
| Z.U.A. Warsi | Fluid Dynamics; Theoretical and Computational Approaches | Taylor & Francis | 2006 |
| Y. A. Cengel and J. M. Cimbala | Fluid Mechanics; Fundamentals and Applications | McGraw Hill | 2006 |
Scalar, vector and tensor fields
Scalars, vectors, and matrices are concepts that may have been introduced to the student in a course in linear algebra. Here, scalar, vector, and tensor fields are entities that are defined over some region of 3-D space and time. It is implicit that they are a function of the spatial coordinates and time, i.e.,
φ
=
φ
(
x
,
y
,
z
,
t
)
=
φ
(
x
,
t
)
. The spatial coordinates are expressed as Cartesian coordinates in this class. However, vectors and tensors are physical entities that are independent of the choice of spatial coordinates even though their components depend on the choice of coordinates.
Scalar fields have a single number, a scalar, at each point in space. An example is the temperature of a body. The temperature field is usually expressed visually by a contour map showing curves of constant temperature or isotherms. An alternative visual display of a scalar field is a color map with the value of the scalar scaled to a gray scale, hue, or saturation. The values of the scalar field are continuous with the exception of definable surfaces of discontinuity. An example is the density of two fluids separated by an interface. Media that are chaotic and discontinuous on a microscopic scale may be described by an average value in a representative elementary volume that is large compared to the microscopic heterogeneity but small compared to macroscopic variations. An example is the porosity of a porous solid.
Vector fields have a magnitude and direction associated with each point in space. An example is the velocity field of a fluid in motion. Vector fields in two dimensions can be visually expressed as field lines that are everywhere tangent to the vector field and whose separation quantifies the magnitude of the field. Streamlines are the field lines of the velocity field. Alternatively, a vector field in two dimensions can be visually expressed by arrows whose directions are parallel to the vector and having a width and/or length that scales to the magnitude of the vector. These graphical representations of vector fields are not useful in three dimensions. In general, a vector field in 3-D can be expressed in terms of its components projected on to the axis of a coordinate system. Thus, a vector field may have different components when projected on to different coordinate systems. Since a vector is a physical entity, the components in different frames of reference transform by prescribed rules. The position of a point in space relative to an origin is a vector defined by the distance and direction. Special vectors having a magnitude of unity are called unit vectors and are used to define a direction such as coordinate directions or the normal direction to a surface. We will denote vectors with bold face letters, e.g., v, x, or n.
Tensors are physical entities associated with two directions. For example, the stress tensor represents the force per unit area, each of which are directional quantities. The velocity gradient is a tensor. Transport coefficients, such as the thermal conductivity, are tensors, which transform a potential gradient to a flux, each of which are vectors. The components of a tensor in a particular coordinate system are represented by a 3×3 matrix. Since the tensor is a physical entity that is independent of the coordinate system, the components must satisfy certain transformation rules between coordinate systems. In particular, a set of three directions called the principal directions can be found to transform the components of the tensor to a diagonal matrix. This corresponds to finding the eigenvectors of a matrix and the components correspond to the eigenvalues. Bold face letters will also denote tensors. The stress tensor will be denoted by T or τ, depending on whether discussing Aris or BSL, respectively.
Curves, surfaces, and volumes
We will be dealing with regions of space, V, having volume that may be bound by surfaces, S, having area. Regions of the surface may be bound by a closed curve, C, having length.
Surfaces are defined by one relationship between the spatial coordinates.
Alternatively, a pair of surface coordinates,
u1,
u2 can define a surface.
Each point on the surface that has continuous first derivatives has associated with it the normal vector, n, a unit vector that is perpendicular or normal to the surface and is outwardly directed if it is a closed surface. Fluid-fluid interfaces need to also be characterized by the mean curvature, H, at each point on the surface to describe the normal component of the momentum balance across the interface. The flux of a vector, f, across a differential element of the surface is denoted as follows, i.e. the normal component of the flux vector multiplied by the differential area.
Curves are defined by two relationships between the spatial coordinates or by the intersection of two surfaces.
Alternatively, a curve in space can be parameterized by a single parameter, such as the distance along the curve, s or time, t.
(1.5)
x
=
x
(
s
)
The tangent vector is a unit vector that is tangent to each point on the curve.
(1.6)
τ
=
d
x
(
s
)
/
d
s
The component of a vector, f, tangent to a differential element of a curve is denoted as follows.
If the parameter along the curve is time, the differential of position with respect to time is the velocity vector and the differential of velocity is acceleration.
Scalars, vectors, and tensors are physical entities that are independent of the choice of coordinate systems. However, the components of vectors and tensors depend on the choice of coordinate systems. The algebra and calculus of vectors and tensors will be illustrated here with Cartesian coordinate systems but these operations are valid with any coordinate system. The student is suggested to read Aris to learn about curvilinear coordinate systems. Bird, Stewart, and Lightfoot express the components of the relevant vector and tensor equations in Cartesian, cylindrical polar, and spherical polar coordinate systems.
Cartesian coordinates have coordinate axes that have the same direction in the entire space and the coordinate values have the units of length. Curvilinear coordinates, in general, may have coordinate axis that are in different directions at different locations in space and have coordinate values that may not have the units of length, e.g., θ in the cylindrical polar system. If (
y1,
y2,
y3) are Cartesian coor