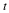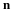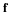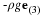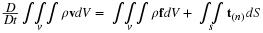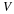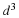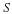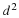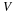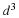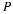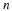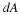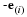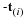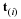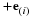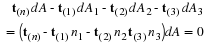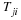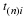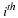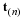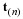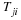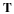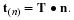Chapter 2. Cartesian Vectors and Tensors: Their Algebra
| Definition of a vector |
| Examples of vectors |
| Scalar multiplication |
| Addition of vectors – coplanar vectors |
| Unit vectors |
| A basis of non-coplanar vectors |
| Scalar product – orthogonality |
| Directional cosines for coordinate transformation |
| Vector product |
| Velocity due to rigid body rotations |
| Triple scalar product |
| Triple vector product |
| Second order tensors |
| Examples of second order tensors |
| Scalar multiplication and addition |
| Contraction and multiplication |
| The vector of an antisymmetric tensor |
| Canonical form of a symmetric tensor |
Reading Assignment: Chapter 2 of Aris, Appendix A of BSL
The algebra of vectors and tensors will be described here with Cartesian coordinates so the student can see the operations in terms of its components without the complexity of curvilinear coordinate systems.
Suppose
xi , i.e., (
x1,
x2,
x3), are the Cartesian coordinates of a point
P
in a frame of reference, 0123. Let  be another Cartesian frame of reference with the same origin but defined by a rigid rotation. The coordinates of the point P in the new frame of reference is
be another Cartesian frame of reference with the same origin but defined by a rigid rotation. The coordinates of the point P in the new frame of reference is 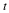 where the coordinates are related to those in the old frame as follows.
where the coordinates are related to those in the old frame as follows.
where lij are the cosine of the angle between the old and new coordinate systems. Summation over repeated indices is understood when a term or a product appears with a common index.
- Definition:
Cartesian Vector
A Cartesian vector, a, in three dimensions is a quantity with three components
a1,
a2,
a3 in the frame of reference 0123, which, under rotation of the coordinate frame to
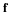 , become components
, become components
 , where
, where
()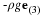
In Cartesian coordinates, the length of the position vector of a point from the origin is equal to the square root of the sum of the square of the coordinates. The magnitude of a vector, a, is defined as follows.
A vector with a magnitude of unity is called a unit vector. The vector, a/|a|, is a unit vector with the direction of a. Its components are equal to the cosine of the angle between a and the coordinate axis. Some special unit vectors are the unit vectors in the direction of the coordinate axis and the normal vector of a surface.
If α is a scalar and a is a vector, the product αa is a vector with components, αai, magnitude α|a|, and the same direction as a.
Addition of vectors – Coplanar vectors
If a and b are vectors with components ai and bi, then the sum of a and b is a vector with components, ai+bi.
The order and association of the addition of vectors are immaterial.
The subtraction of one vector from another is the same as multiplying one by the scalar (-1) and adding the resulting vectors.
If a and b are two vectors from the same origin, they are colinear or parallel if one is a linear combination of the other, i.e., they both have the same direction. If a and b are two vectors from the same origin, then all linear combination of a and b are in the same plane as a and b, i.,e., they are coplanar. We will prove this statement when we get to the triple scalar product.
The unit vectors in the direction of a set of mutually orthogonal coordinate axis are defined as follows.
The suffixes to e are enclosed in parentheses to show that they do not denote components. A vector, a, can be expressed in terms of its components, (a1, a2,a3) and the unit vectors.
This equation can be multiplied and divided by the magnitude of a to express the vector in terms of its magnitude and direction.
where λi are the directional cosines of a.
A special unit vector we will use often is the normal vector to a surface, n. The components of the normal vector are the directional cosines of the normal direction to the surface.
Scalar product – Orthogonality
The scalar product (or dot product) of two vectors, a and b is defined as
where θ is the angle between the two vectors. If the two vectors are perpendicular to each other, i.e., they are orthogonal, then the scalar product is zero. The unit vectors along the Cartesian coordinate axis are orthogonal and their scalar product is equal to the Kronecker delta.
The scalar product is commutative and distributive. The cosine of the angle measured from a to b is the same as measured from b to a. Thus the scalar product can be expressed in terms of the components of the vectors.
The scalar product of a vector with itself is the square of the magnitude of the vector.
The most common application of the scalar product is the projection or component of a vector in the direction of another vector. For example, suppose n is a unit vector (e.g., the normal to a surface) the component of a in the direction of n is as follows.
Directional Cosines for Coordinate Transformation
The properties of the directional cosines for the rotation of the Cartesian coordinate reference frame can now be easily illustrated. Suppose the unit vectors in the original system is
e
(
i
)
and in the rotated system is  . The components of the unit vector,
. The components of the unit vector, 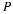 , in the original reference frame is
lij. This can be expressed as the scalar product.
, in the original reference frame is
lij. This can be expressed as the scalar product.
Since
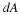 is a unit vector, it has a magnitude of unity.
is a unit vector, it has a magnitude of unity.
Also, the axis of a Cartesian system are orthorgonal.
The vector product (or cross product) of two vectors, a and b, denoted as a×b, is a vector that is perpendicular to the plane of a and b such that a, b, and a×b form a right-handed system. (i.e., a, b, and a×b have the orientation of the thumb, first finger, and third finger of the right hand.) It has the following magnitude where θ is the angle between a and b.
The magnitude of the vector product is equal to the area of a parallelogram two of whose sides are the vectors a and b.
Since the vector product forms a right handed system, the product b×a has the same magnitude but opposite direction as a×b, i.e., the vector product is not commutative,
The vector product of a vector with itself or with a parallel vector is zero or the null vector, i.e., a×a=0. A quantity that is the negative of itself is zero. Also, the angle between parallel vectors is zero and thus the sine is zero.
Consider the vector product of the unit vectors. They are all of unit length and mutually orthogonal so their vector products will be unit vectors. Remembering the right-handed rule, we therefore have
The components of the vector product can be expressed in terms of the components of a and b and applying the above relations between the unit vectors.
The permutations of the indices and signs in the expression for the vector product may be difficult to remember. Notice that the expression is the same as that for the expansion of a determinate of the matrix,
Expansion of determinants are aided by the permutation symbol,
εijk.
The expression for the vector product is now as follows.
Velocity due to rigid body rotations
We will show that the velocity field of a rigid body can be described by two vectors, a translation velocity, v(t), and an angular velocity, ω. A rigid body has the constraint that the distance between two points in the body does not change with time. The translation velocity is the velocity of a fixed point, O, in the body, e.g., the center of mass. Now consider a new reference frame (coordinate system) with the origin at point O that is translating with respect to the original reference frame with the velocity v(t). The rotation of the body about O is defined by the angular velocity, ω, i.e., with a magnitude ω and a direction of the axis of rotation, n, such that the positive direction is the direction that a right handed screw advances when subject to the rotation, .ω=ω n. Consider a point P not on the axis of rotation, having coordinates x in the new reference frame. The velocity of P in the new reference frame has a magnitude equal to the product of ω and the radius of the point P from the axis of rotation. This radius is equal to the magnitude of x and the sine of the angle between x and ω, i.e., |x| sinθ. The velocity of point P in the new reference frame can be expressed as
The velocity field of any point of the rigid body in the original reference frame is now
Since this equation is valid for any pair of points in the rigid body, the relative velocity Δv between a pair of points separated by Δx can be expressed as follows.
Conversely, if the relative velocity between any pair of points is described by the above equation with the same value of angular velocity, then the motion is due to a rigid body rotation.
The triple scalar product is the scalar product of the first vector with the vector product of the other two vectors. It is denoted as (abc) or [abc].
Recall that b×c has a magnitude equal to the area of a parallelogram with sides b and c and a direction normal to the plane of b and c. The scalar product of this normal vector and the vector a is equal to the altitude of the parallelepiped with a common origin and sides a, b, and c. The triple scalar product has a magnitude equal to the volume of a parallelepiped with a common origin and sides a, b, and c. The sign of the triple scalar product can be either positive or negative. If a, b, and c are coplanar, then the altitude of the parallelepiped is zero and thus the triple scalar product is zero.
The triple scalar product can be expressed in terms of the components by using the earlier definitions of the vector product and scalar product.
From the definition of the permutation symbol, the triple scalar product is unchanged by even permutations of a, b, and c but have the opposite algebraic sign for odd permutations. Also, if any two of a, b, and c are identical, then permutation of the two identical vectors results in a triple scalar products that are identical and also opposite in sign. This implies that the triple scalar product is zero if two of the vectors are identical.
The triple vector product of vectors a, b, and c results from the repeated application of the vector product, i.e., a×(b×c). Since b×c is normal to the plane of b and c and a×(b×c) is normal to b×c, a×(b×c) must be in the plane of b and c. It is left as an exercise to show that
A second order tensor can be written as a 3×3 matrix.
A tensor is a physical entity that is the same quantity in different coordinate systems. Thus a second order tensor is defined as an entity whose components transform on rotation of the Cartesian frame of reference as follows.
If Aij=Ajithe tensor is said to be symmetric and a symmetric tensor has only six distinct components. If A<