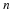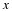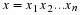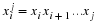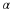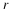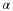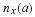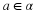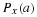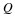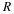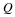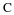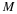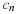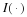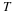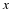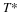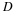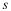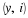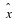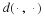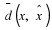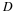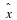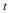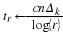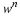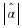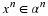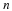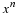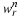The following material appears in most textbooks on information theory
(c.f., Cover and Thomas 1 and references therein).
We include the highlights in order
to make these notes self contained, but skip some details and the proofs.
Consider a sequence 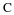 , where xi∈α, α is the alphabet, and
the cardinality of α is r, i.e., |α|=r.
, where xi∈α, α is the alphabet, and
the cardinality of α is r, i.e., |α|=r.
Definition 1 The type of x consists of the empirical probabilities of symbols in x,
where nx(a) is the empirical symbol count,
which is the the number of times that a∈α appears in x.
Definition 2 The set of all possible types is defined as Pn.
Example 2.1.
For an alphabet α={0,1} we have 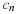 .
In this case, |Pn|=n+1.
.
In this case, |Pn|=n+1.
Definition 3 A type class Tx contains all x'∈αn, such that Px=Px',
Example 2.2.
Consider α=1,2,3 and x=11321.
We have n=5 and the empirical counts are nx=(3,1,1).
Therefore, the type is 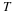 ,
and the type class Tx contains all length-5 sequences with 3 ones, 1 two, and 1 three.
That is, Tx={11123,11132,...,32111}.
It is easy to see that
,
and the type class Tx contains all length-5 sequences with 3 ones, 1 two, and 1 three.
That is, Tx={11123,11132,...,32111}.
It is easy to see that  .
.
Theorem 1 The cardinality of the set of all types satisfies |Pn|≤(n+1)r–1.
The proof is simple, and was given in class.
We note in passing that this bound is loose, but it is good enough for our discussion.
Next, consider an i.i.d. source with the following prior,
We note in passing that i.i.d. sources are sometimes called memoryless.
Let the entropy be
where we use base-two logarithms throughout.
We are studying the entropy 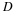 in order to show that it is the fundamental performance limit in lossless compression.
Σ
find me
in order to show that it is the fundamental performance limit in lossless compression.
Σ
find me
We also define the divergence as
It is well known that the divergence is non-negative,
Moreover, D(P∥Q)=0 only if the
distributions are identical.
Claim 1 The following relation holds,
The derivation is straightforward,
Seeing that the divergence is non-negative Equation 2.8,
and zero only if the distributions are equal,
we have Q(x)≤Px(x).
When Px=Q the divergence between them is zero, and we have that 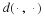 .
.
The proof of the following theorem was discussed in class.
Theorem 2 The cardinality of the type class 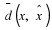 obeys,
obeys,
Having computed the probability of x and cardinality of its type class,
we can easily compute the probability of the type class.
Claim 2 The probability 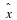 of the type class
of the type class  obeys,
obeys,
Consider now an event A that is a union over 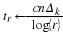 .
Suppose T(Q)⊈A, then A is rare with respect to (w.r.t) the prior Q.
and we have limn→∞Q(A)=0. That is, the probability is
concentrated around Q. In general, the probability assigned by the prior Q
to an event A satisfies
.
Suppose T(Q)⊈A, then A is rare with respect to (w.r.t) the prior Q.
and we have limn→∞Q(A)=0. That is, the probability is
concentrated around Q. In general, the probability assigned by the prior Q
to an event A satisfies
where we denote 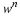 when
when  .
.
2.3. Fixed and Variable Length Coding
Fixed to fixed length source coding: As before, we have a sequence x of length n, and each element of x is from the alphabet α.
A source code maps the input xn∈rn to a set of 2Rn bit vectors, each of length Rn.
The rate R quantifies the number of output bits of the code per input element of x.[]
That is, the output
of the code consists of nR bits. If n and R is fixed, then we call this a fixed to fixed length source code.
The decoder processes the nR bits and yields  . Ideally we have that
. Ideally we have that  ,
but if 2nR<rn then
there are inputs that are not mapped to any output, and
,
but if 2nR<rn then
there are inputs that are not mapped to any output, and 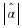 may differ from x.
Therefore, we want
may differ from x.
Therefore, we want  to be small.
If R is too small, then the error probability will go to 1. On the other hand, sufficiently large R will drive
this error probability to 0 as n is increased.
to be small.
If R is too small, then the error probability will go to 1. On the other hand, sufficiently large R will drive
this error probability to 0 as n is increased.
If log(r)>R and 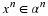 is vanishing as n is increased, then we are compressing, because
2log(r)n=rn>2Rn, where rn is the number of possible inputs x
and there are 2Rn possible outputs.
is vanishing as n is increased, then we are compressing, because
2log(r)n=rn>2Rn, where rn is the number of possible inputs x
and there are 2Rn possible outputs.
What is a good fixed to fixed length source code? One option is to map 2Rn–1 outputs to inputs
with high probabilities, and the last output can be mapped to a “don't care" input.
We will discuss the performance of this style of code.
An input x∈rn is called δ-typical if Q(x)>2–(H+δ)n. We denote the set of δ-typical
inputs by TQ(δ), this set includes
the type classes whose empirical probabilities are equal (or closest) to the true prior Q(x).
Note that for each type class Tx, all inputs x'∈Tx in the type class have the same probability, i.e., 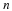 .
Therefore, the set TQ(δ) is a union of type classes, and can be thought of as an event A
(Section 2.2) that contains type classes consisting of high-probability sequences.
It is easily seen that the event A contains the true i.i.d. distribution Q, because sequences whose empirical probabilities
satisfy Px=Q also satisfy
.
Therefore, the set TQ(δ) is a union of type classes, and can be thought of as an event A
(Section 2.2) that contains type classes consisting of high-probability sequences.
It is easily seen that the event A contains the true i.i.d. distribution Q, because sequences whose empirical probabilities
satisfy Px=Q also satisfy
(2.14)
Q
(
x
)
=
2
–
H
n
>
2
–
(
H
+
δ
)
n
.
Using the principles discussed in Section 2.2, it is readily seen that
the probability under the prior Q of the inputs in TQ(δ) satisfies
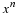 when n→∞.
Therefore, a code C that enumerates TQ(δ) will encode x correctly with high probability.
when n→∞.
Therefore, a code C that enumerates TQ(δ) will encode x correctly with high probability.
The key question is the size of C, or the cardinality of TQ(δ).
Because each x∈TQ(δ) satisfies Q(x)>2(–H+δ)n, and
∑x∈TQ(δ)Q(x)≤1, we have |TQ(δ)|<2(H+δ)n.
Therefore, a rate R≥H+δ allows near-lossless coding,
because the probability of error vanishes
(recall that 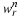 , where (·)C denotes the complement).
, where (·)C denotes the complement).
On the other hand, a rate R≤H–δ will not allow lossless coding, and the probability of error will go to 1.
We will see this intuitively. Because the type class whose empirical prob