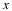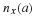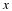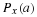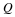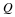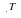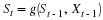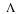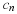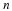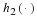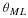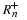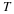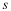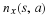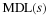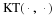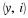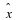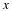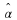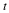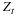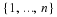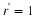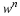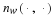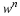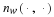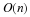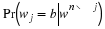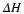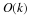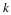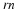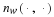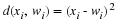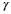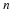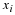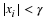Chapter 3. Source models*
2013/05/21 14:36:08 -0500
For i.i.d. sources, 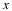 ,
which means that the divergence increases linearly with n.
Not only does the divergence increase, but it does so by a constant per symbol.
Therefore, based on typical sequence concepts that we have seen, for an xn generated by P1,
its probability under P2 vanishes. However, we can construct a distribution Q whose divergence
with both P1 abd P2 is small,
,
which means that the divergence increases linearly with n.
Not only does the divergence increase, but it does so by a constant per symbol.
Therefore, based on typical sequence concepts that we have seen, for an xn generated by P1,
its probability under P2 vanishes. However, we can construct a distribution Q whose divergence
with both P1 abd P2 is small,
We now have for P1,
On the other hand, 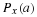 Equation 2.8,
and so
Equation 2.8,
and so
By symmetry, we see that Q is also close to P2 in the divergence sense.
Intuitively, it might seem peculiar that Q is close to
both P1 and P2 but they are far away from each other (in divergence terms). This intuition
stems from the triangle inequality, which holds for all metrics. The contradiction is resolved by realizing
that the divergence is not a metric, and it does not satisfy the triangle inequality.
Note also that for two i.i.d. distributions P1 and P2, the divergence
is linear in n.
If Q were i.i.d., then 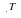 must also be linear in n. But the divergence is not increasing
linearly in n, it is upper bounded by 1. Therefore, we conclude that Q(·) is not an i.i.d.
distribution. Instead, Q is a distribution that contains memory, and there is dependence in Q
between collections of different symbols of x in the sense that they are either all drawn from P1
or all drawn from P2.
To take this one step further, consider K sources with
must also be linear in n. But the divergence is not increasing
linearly in n, it is upper bounded by 1. Therefore, we conclude that Q(·) is not an i.i.d.
distribution. Instead, Q is a distribution that contains memory, and there is dependence in Q
between collections of different symbols of x in the sense that they are either all drawn from P1
or all drawn from P2.
To take this one step further, consider K sources with
then in an analogous manner to before it can be shown that
Sources with memory: Instead of the memoryless (i.i.d.) source,
let us now put forward a statistical model with memory,
Stationary source: To understand the notion of a stationary source, consider an infinite stream of symbols,
...,x–1,x0,x1,....
A complete probabilistic description of a stationary distribution is given by the collection of all
marginal distribution of the following form for all t and n,
For a stationary source, this distribution is independent of t.
Entropy rate: We have defined the first order entropy of an i.i.d. random variable Equation 2.6,
and let us discuss more advanced concepts for sources with memory.
Such definitions appear in many standard textbooks, for example that by
Gallager 1.
The order-n entropy is defined,
The entropy rate is the limit of order-n entropy, 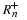 .
The existence of this limit will be shown soon.
.
The existence of this limit will be shown soon.
Conditional entropy is defined similarly to entropy as the expectation of the log of
the conditional probability,
where expectation is taken over the joint probability space, 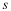 .
.
The entropy rate also satisfies 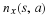 .
.
Theorem 3
For a stationary source with bounded first order entropy, H1(x)<∞, the following hold.
The conditional entropy 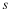 is monotone non-increasing in n.
is monotone non-increasing in n.
The order-n entropy is not smaller than the conditional entropy,
The order-n entropy Hn(x) is monotone non-increasing.
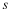 .
.
Proof. Part (1):
Part (2):
Part (3): This comes from the fist equality in the proof of (2),
because we have the average of a monotonely non-increasing sequence.
Part (4): Both sequences are monotone non-increasing (parts (1) and (3)) and bounded below (by zero). Therefore, they both have a limit. Denote 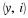 and
and 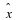 .
.
Owing to part(2), 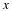 . Therefore, it suffices to prove
. Therefore, it suffices to prove 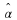 .
.
Now fix n and take the limit for large m. The inequality 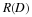 appears,
which proves that both limits are equal.
appears,
which proves that both limits are equal.
Coding theorem: Theorem 3 yields for fixed to variable length coding
that for a stationary source, there exists a lossless code such that the compression
rate ρn obeys,
This can be proved, for example, by choosing 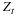 ,
which is a Shannon code.
As n is increased, the compression rate ρn converges to the entropy rate.
,
which is a Shannon code.
As n is increased, the compression rate ρn converges to the entropy rate.
We also have a converse theorem for lossless coding of stationary sources. That is,
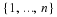 .
.
3.1. Stationary Ergodic Sources
Consider the sequence 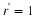 . Let x'=Sx denote a step ∀n∈Z, xn'=xn+1,
where Sxi takes i steps. Let fk(x) be a function that operates on coordinates
. Let x'=Sx denote a step ∀n∈Z, xn'=xn+1,
where Sxi takes i steps. Let fk(x) be a function that operates on coordinates 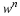 .
An ergodic source has the property that empirical averages converge to statistical averages,
.
An ergodic source has the property that empirical averages converge to statistical averages,
In block codes we want
We will be content with convergence in probability, and a.s. convergence is better.
Theorem 4
Let X be a stationary ergodic source with H1(x)<∞,
then for every ϵ>0,δ>0, there exists n0(δ,ϵ) such that
∀n≥n0(δ,ϵ),
where 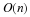 .
.
The proof of this result is quite lengthy. We discussed it in detail, but skip it here.
Theorem 4 is called the ergodic theorem of information theory or the ergodic theorem of entropy.
Shannon (48') proved convergence in probability for stationary ergodic Markov sources.
McMillan (53') proved L1 convergence for stationary ergodic sources.
Brieman (57'/60') proved convergence with probability 1 for stationary ergodic sources.
3.2. Parametric Models of Information Sources
In this section, we will discuss several parametric models and see what their entropy rate is.
Memoryless sources: We have seen for memoryless sources,
where there are r–1 parameters in total,
(3.21)
θ
=
{
p
(
a
)
,
a
=
1
,
2
,
.
.
.
,
r
–
1
}
,
the parameters are denoted by θ,
and α={1,2,...,r} is the alphabet.
Markov sources:
The distribution of a Markov source is defined as
where n≥k. We must define 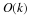 initial probabilities and transition probabilities,
initial probabilities and transition probabilities, 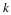 . There are rk–1 initial probabilities and (r–1)rk transition probabilities, giving a total of rk+1–1 parameters. Note that
. There are rk–1 initial probabilities and (r–1)rk transition probabilities, giving a total of rk+1–1 parameters. Note that
Therefore, the space of Markov sources covers the stationary ergodic sources in the limit of large k.
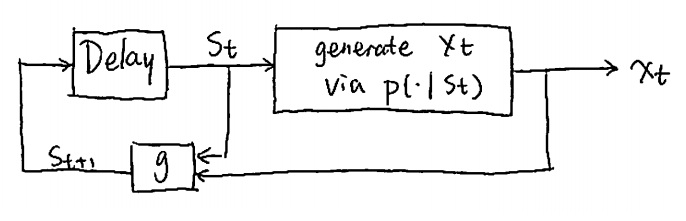
Unifilar sources:
For unifilar sources, it is possible to reconstruct the set of states that a source went through by looking at the output sequence. In the Markov case we have 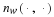 , but in general it may be more complicated to determine the state.
, but in general it may be more complicated to determine the state.
To put us on a concrete basis for analysis of unifilar sources, consider a source with M states, S={1,2,...,M}, and an alphabet α={1,2,...,r}. In each time step, the source outputs a symbol and moves to a new state. Denote the output sequence by x=x1x2⋯xn, and the state sequence by s=s1s2⋯sn, where si∈S and xi∈α. Denote also
This is a first-order time-homogeneous Markov source.
The probability that the next symbol is a follows,
There exists a deterministic function,
this is called the next state function.
Given that we start at some state S1=s1, the probability for the sequence of
states s1,...,sn is given by
Note the relation
To summarize, unifilar sources can be described by a state machine style of
diagram as illustrated in Figure 3.1.
Given that an initial state was fixed, a unifilar source with M states and an alphabet of size r can be expressed with M(r–1) parameters. If the initial state is a random variable, then there are M–1 parameters that define probabilities for the initial state, giving M(r–1)+M–1=Mr–1 parameters in total. In the Markov case, we have M=rk, it is a special type of unifilar source.
Example 3.1.
For the unifilar source that appears in Figure 3.2, the states can be discerned from the output sequence. Let us follow up on this example while discussing more properties of unifilar sources.