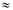Chapter Four
4. GENERAL PRINCIPLES OF SECONDARY ACTIVE TRANSPORTER FUNCTION
Oliver Beckstein*, Fiona Naughton
Department of Physics, Arizona State University, Tempe AZ 85287, USA
ABSTRACT
Transport of ions and small molecules across the cell membrane against electrochemical gradients is catalyzed by integral membrane proteins that use a source of free energy to drive the energetically uphill flux of the transported substrate. Secondary active transporters couple the spontaneous influx of a “driving” ion such as Na+ or H+ to the flux of the substrate. The thermodynamics of such cyclical non-equilibrium systems are well understood and recent work has focused on the molecular mechanism of secondary active transport. The fact that these transporters change their conformation between an inward-facing and outward-facing conformation in a cyclical fashion, called the alternating access model, is broadly recognized as the molecular framework in which to describe transporter function. However, only with the advent of high resolution crystal structures and detailed computer simulations has it become possible to recognize common molecular-level principles between disparate transporter families. Inverted repeat symmetry in secondary active transporters has shed light on how protein structures can encode a bi-stable two-state system. More detailed analysis (based on experimental structural data and detailed molecular dynamics simulations) indicates that transporters can be understood as gated pores with at least two coupled gates. These gates are not just a convenient cartoon element to illustrate a putative mechanism but map to distinct parts of the transporter protein. Enumerating all distinct gate states naturally includes occluded states in the alternating access picture and also suggests what kind of protein conformations might be observable. By connecting the possible conformational states and ion/substrate bound states in a kinetic
Keywords: membrane protein, transporter, symmetry, molecular mechanisms
* Direct all correspondence to Dr. Oliver Beckstein, Department of Physics, Arizona State University, Tempe, AZ, USA. E-mail: oliver.beckstein@asu.edu. model, a unified picture emerges in which symporter, antiporter, and uniporter function are extremes in a continuum of functionality.
4.1. INTRODUCTION
Active transporters are integral membrane proteins that move substrate through the membrane against an electrochemical gradient by using a source of free energy. They are broadly classified as primary and secondary active transporters, depending on the free energy source (Mitchell, 1967). Primary active transporters harness chemical reactions (e.g., phosphorylation by ATP) or light. Some examples are the sodium-potassium pump (Na/K ATPase) (Morth et al., 2007), the rotary F0F1-ATPase and the light-driven proton pump bacteriorhodopsin (Buch-Pedersen et al., 2009), complex I in the respiratory chain (Sazanov, 2015), or ATP-driven ABC transporters such as p-glycoprotein (Lespine et al., 2009).
Secondary transport is driven by an electrochemical gradient in a driving ion, namely sodium or protons. Examples are neurotransmitter transporters SERT (serotonin) and DAT (dopamine) (Gouaux, 2009), sodium-proton exchangers (NHE) (Fuster and Alexander, 2014), the calcium exchanger (Ottolia et al., 2007), and AE1, the anion exchanger in red blood cells also known as Band 3 (Västermark et al., 2014). Secondary active transporters can be divided into two classes based on their physiological behavior (Mitchell, 1967). Symporters move their substrate in parallel with the driving ion (Figure 1A). Both driving ion and substrate are bound at the same time and move in the same direction. One part of the transport cycle consists of the movement of the substrate- and ion-free (apo) transporter.
In the antiporter transport cycle (Figure 1B), the driving ion is bound during one leg of the cycle while the substrate is bound in the other leg and is transported in the opposite direction.
Variations of the above scheme are common, though. For instance, many symporters transport another ion back instead of the apo leg of the transport cycle. Sometimes, the driving ion is effectively part of the substrate as in the AdiC transporter (Fang et al., 2009), which exchanges L-arginine with its decarboxylated product agmatine to effectively export protons.
A third class of related transporters consists of non-coupled transporters. These uniporters facilitate diffusion through the membrane. Although we specifically focus on active transporters, the discussion on transport cycles (Section 6) will make clear that the uniporters are closely related to active transporters and it is plausible that small changes in the protein may convert between the two.
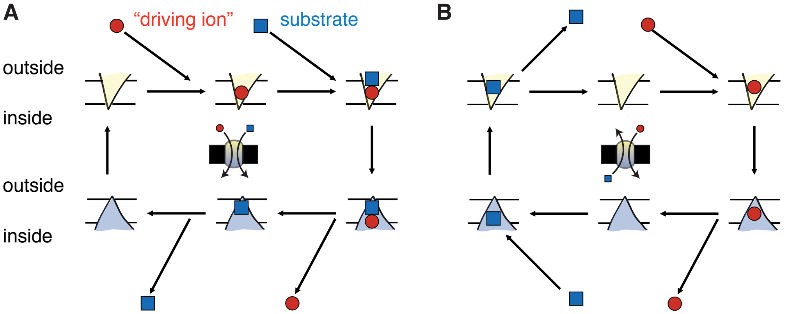
Figure 1. Secondary active transport cycles.
Schematic transport cycle of A a symporter (transport of substrate and driving ion in the same direction) and B an antiporter (transport in opposite directions). The central cartoon summarizes the physiological function. The V-shaped triangle symbolizes a membrane-embedded transporter protein in the outward facing conformation in which its binding sites are accessible from the outside. The hatshaped triangle indicates the inward facing conformation. The driving ion is drawn as a circle while the transported substrate is shown as a square. The predominant direction of reactions is shown by arrows, with horizontal arrows indicating binding/unbinding and vertical arrows conformational transitions. The order of binding and unbinding events and the stoichiometry of substrate to driving ions may differ from this cartoon.
In this chapter we focus on overarching principles that are common across almost all secondary active transporters. We begin with the alternating access model which provides the “standard model” for explaining transporter function in a structural context (Section 2). Although evolution always finds ways to add a few exceptions to common rules (for instance, there are a few transporters that do not appear to follow the classical alternating access model), the physical principles under which transporters operate are not negotiable. Transporters function out of equilibrium as “physical enzymes” that catalyze transport by free energy transduction through cyclic processes (Section 3). Ten years ago, a remarkable insight was found into the evolutionary mechanism that can generate protein structures that can switch between the two states of the alternating access model: transporters contain so-called inverted repeat sequences that fold into structures with an internal pseudo two-fold symmetry. This symmetry is broken to generate two different conformations, as discussed in Section 4. A complimentary view of transporters is that of a pore with multiple coupled gates; originally motivated by the description of ion channels as pores with a single gate, this cartoon model has proven valuable because transporters actually contain physical components that perform the functions of gates, as will be shown with selected examples in Section 5. When the alternating access/gated pore model is considered together with the cycle view of transport, a simple unified picture emerges that describes symporters, antiporters, and uniporters as ideals in a spectrum of functionality (Section 6).
4.2. THE ALTERNATING ACCESS MODEL
The alternating access model in its basic form was described by Jardetzky (1966) as a polymer molecule that contains binding sites for substrate and is able to assume two different conformations that alternatingly expose the binding sites to the interior and the exterior. The idea of a cyclical process facilitated by a molecule that changes accessibility was expressed by Mitchell (1967) in his “circulating carrier” model. Together these models describe in abstract terms a basic framework or model to understand driven transport across the cell membrane. The key insight was that coupling of two fluxes (substrate and driving ion) could be accomplished by binding to different conformations of the same molecule as discussed in more detail in the next Section 3. In particular, it is physically not possible to move substrate against a gradient through a continuous pore, i.e., one that is simultaneously accessible from both sides, regardless of any energy consuming mechanism to open or close the pore (Tanford, 1983). The consequence of this insight is that transporters cannot function if continuous pores are formed through the membrane. The alternating access model with its two distinct states provides a conceptual framework that avoids pore formation. However, it requires that a membrane protein is able to change between different conformations on the sub-millisecond time scale1, a speed that is easily achievable for macromolecular conformational changes (Henzler-Wildman and Kern, 2007; Schwartz and Schramm, 2009). The alternating access model also does not give any insights into the actual molecular structure of a transporter except the general requirement that substrate and ion binding sites must switch accessibility in different conformations. In order to obtain deeper mechanistic insights actual atomic-scale structures of transporters in multiple conformations are needed.
The first secondary active transporter for which the major states in the transport cycle were resolved at atomic resolution was the sodium-coupled symporter Mhp1, a member of the nucleobase-cation-symporter 1 (NCS1) family (Weyand et al., 2011; Jackson et al., 2013; Patching, 2018). The structures of wild-type Mhp1 revealed a sodium binding and a substrate binding site deep at the center of the transporter, roughly at the membrane midplane (Weyand et al., 2008). In one structure, these binding sites were accessible from the extracellular side, making this the outward facing (OF) conformation as shown in Figure 2.

Figure 2. Conformations of the nucleobase/sodium-coupled symporter Mhp1 from X-ray crystallography.
A Outward-facing open conformation (PDB ID 2JLN) (Weyand et al., 2008). B Outward-facing occluded conformation with bound substrate benzylhydantoin (PDB ID 4D1B (Simmons et al., 2014); this structure superseded the original 2JLO structure (Weyand et al., 2008) but the structural differences are small). C Inward-facing open conformation (PDB ID 2X79; (Shimamura et al., 2010)). The approximate position in the membrane is indicated by the gray rectangle in the background. The two cartoons under A and C indicate the two states of the classical alternating access model as used in Figure 1.
Shimamura et al. (2010) managed to crystallize wild-type Mhp1 in an inward facing (IF) conformation in which the binding sites were exposed to the intracellular side. Together they represent the two key conformations required by the alternating access model. A third conformation was also found: in this occluded conformation the binding sites were not accessible from any compartment (Weyand et al., 2008; Simmons et al., 2014). The alternating access model does not require such a conformation. As will be argued in Section 5, such occluded states are a necessary consequence of a molecular architecture in which the alternating access conformations are formed by gate domains.
The hallmark of the alternating access mechanism are relatively large conformational changes in protein conformation and these appear to exist in many secondary transporters for which this mechanism remains the standard structural framework in which to understand transporter function (Boudker and Verdon, 2010; Law, Maloney and Wang, 2008; Forrest and Rudnick, 2009; Gouaux, 2009; Krishnamurthy, Piscitelli and Gouaux, 2009; Abramson and Wright, 2009; Boudker and Verdon, 2010; Kaback et al., 2011; Forrest, Krämer and Ziegler, 2011; Schweikhard and Ziegler, 2012; Henzler-Wildman, 2012; Yan, 2013; Shi, 2013; Slotboom, 2014; Diallinas, 2014; Li et al., 2015; Drew and Boudker, 2016; Bai, Moraes and Reithmeier, 2017; Kazmier, Claxton and Mchaourab, 2017; Patching, 2018; Henderson, Fendler, and Poolman, 2019).
Although the alternating access model is the canonical model for active transporters, some transporters appear not to be described well within this framework. For example, chloride/proton antiporters are currently understood to function by small changes in a central glutamate residue that alternatingly binds chloride and protons (Miller, 2006; Accardi, 2015) and do not require the large conformational change—the “alternating access transition”—that is generally taken to be a key step in the classical alternating access model. However, it could be argued that the fundamental principle of alternating access and the need to maintain a pathway that cannot directly conduct ions and substrate always has to be maintained in order to support the cyclical reactions that are required for energy transduction (see the next Section 3) even though different models are also sometimes discussed (Klingenberg, 2007; Naftalin, 2010).
4.3. THERMODYNAMICS AND CYCLES
Transport is driven by spontaneous influx of a driving ion. The free energy dissipation from flowing down its electrochemical gradient is coupled to the vectorial transport of a substrate molecule or ion. Hill (1989) clearly explained the principle of free energy transduction in transporters (and enzymes) through a cyclic process that tightly couples driving ion flux and substrate flux. Following his treatment, we will first qualitatively explain how a cyclical process that operates out of equilibrium transduces energy. We will then briefly revisit the thermodynamic driving forces of the process in order to motivate the idea that transporters are really enzymes that catalyze transport.
4.3.1. Transport is a non-equilibrium process
Consider, for instance, a hypothetical antiporter that uses one driving ion (red circle in Figure 3A) to move one substrate molecule (blue square). We initially imagine the system to exist in equilibrium, i.e., the net fluxes between all states are zero, also known as the detailed balance condition. The inside and outside populations i of particles are in Nernst equilibrium, i.e., when considering the concentrations on either side of the membrane and the membrane potential, no net flux of particles would occur if a pore selective for species i were opened in the membrane.2 For example, the binding of a driving ion to the transporter in the outward facing conformation is the equilibrium reaction
T1 + I  T2 : I (1)
T2 : I (1)
and the isomerization between outward facing and inward facing conformation (the alternating access transition) is
T2 : I  T3 : I (2)
T3 : I (2)
Because all individual fluxes are zero, no net transport takes place. On average, for every substrate molecule that is moved from inside to outside in a given unit of time, the same number of molecules are moved from the outside to the inside.
We now perturb the system away from equilibrium by increasing the outside concentration of the driving ion, as indicated by the larger number of driving ions in Figure 3B. Following Le Chatelier’s principle, the equilibrium of the binding reaction Eq. 1 is moved as to increase the concentration of products (Dill and Bromberg, 2003), i.e., the number of ion-loaded transporters T2 : I increases above its equilibrium value. Because the reactants (inputs) of the isomerization reaction Eq. 2 are provided by the products (output) of the binding reaction Eq. 1, which have increased, Le Chatelier’s principle equally applies to the isomerization and pushes this equilibrium towards the ion-loaded inward facing conformation, T3 : I.
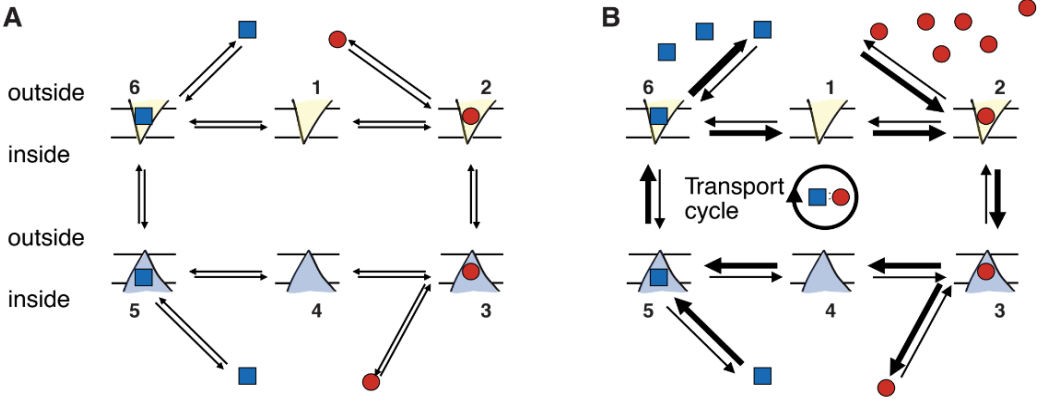
Figure 3. Transport by an antiporter is a cyclical out-of-equilibrium process. A Equilibrium—all concentrations are at equilibrium values and all reactions obey detailed balance. B Out-of-equilibrium—the outside ion concentration is raised over its equilibrium value, which leads to moving all states out of equilibrium. The states are numbered so that one can refer to, say, the outward facing apo state (neither ion nor substrate bound) of the transporter as T1 or the inward facing, substrate-bound state as T5 : S where the presence of the substrate is included for clarity even though the label “5” includes the presence of the substrate (as opposed to state 4, which does not include it).
The same reasoning is applied to each subsequent reaction and in this way, net flux of substrate from the inside to the outside is induced in steps 5→6. Crucially, the reactions form a cycle so that after the steps 1→2→3→4→5→6→1 the transporter is in exactly the same state as it was before. However, the environment has changed as one ion was transported from the outside to the inside and one substrate was transported from the inside to the outside with 1:1 stoichiometry, as expressed by the transport reaction of the antiporter,3
Iout + Sin → Iin + Sout. (3)
The corresponding reaction of the symporter is
Iout + Sout → Iin + Sin. (4)
Interested readers are referred to Hill (1989) who makes the above reasoning quantitative by considering how the net fluxes between states, which are zero in equilibrium, become biased in one direction when a component is perturbed. Based on reaction kinetics he develops a theory of cycle fluxes that can be applied to arbitrarily complex cycles to compute steady state populations and fluxes. In particular, more realistic transporter schemes contain additional transitions such as the one between the two apo states 1  4, often referred to as leaks or slippage. Such a transition would allow three cycles to become possible: The transport cycle that was just described and two leak cycles: cycle 1
4, often referred to as leaks or slippage. Such a transition would allow three cycles to become possible: The transport cycle that was just described and two leak cycles: cycle 1  2
2  3
3  4
4  1 would dissipate the ionic gradient. Cells spend a substantial amount of their chemical energy to establish the driving ion gradient. In mammals an estimated 19%–28% of ATP are used to power the Na+-K+-ATPase that establishes the transmembrane sodium gradient (Rolfe and Brown, 1997). Therefore, dissipation of the sodium gradient is costly and reduces the organism’s fitness. The other leak cycle 1
1 would dissipate the ionic gradient. Cells spend a substantial amount of their chemical energy to establish the driving ion gradient. In mammals an estimated 19%–28% of ATP are used to power the Na+-K+-ATPase that establishes the transmembrane sodium gradient (Rolfe and Brown, 1997). Therefore, dissipation of the sodium gradient is costly and reduces the organism’s fitness. The other leak cycle 1  6
6  5
5  4
4  1 would run in the opposite direction and let substrate molecules enter the cell, counter to the physiological necessity of the transporter to remove them from the cell. Under physiological conditions, leak cycles must be suppressed by decreasing the rate for slippage transitions such as 1
1 would run in the opposite direction and let substrate molecules enter the cell, counter to the physiological necessity of the transporter to remove them from the cell. Under physiological conditions, leak cycles must be suppressed by decreasing the rate for slippage transitions such as 1  4.
4.
The qualitative discussion makes clear that energy transduction, i.e., the use of the free energy stored in the driving ion gradient, requires a complete cycle that contains both ion and substrate translocation steps. If any part of the cycle is broken, no energy transduction can take place. Thus, energy transduction is a property of complete cycles and not of individual states (Hill, 1989). Therefore, there is no specific step in the cycle that could be described as an “energized” state or a state where energy is “gained by a binding reaction” (Hill and Eisenberg, 1981).
In general, a protein that functions according to the alternating access mechanism cannot function if it presents a continuous, leaky pathway (Tanford, 1983) as this prevents energy coupling. Similarly, non-productive leak cycles also reduce the efficiency of a transporter. Although here we generally discuss ideal, fully efficient cycles to elucidate the basic principles, real transporters leak and therefore their transport stoichiometry is generally not the ideal one (Hill, 1989; Henderson, Fendler and Poolman, 2019). For example, instead of an ideal 1:1 stoichiometry one might measure only 1:0.75, i.e., on average 1.33 driving ions are needed to move one substrate because only 75% of the total flux comes from productive cycles (1:1 stoichiometry) and 25% comes from leak cycles (1:0).
The ion and substrate binding or dissociation steps are necessary components of the cycle because without them the cycle cannot be driven in a specific direction: these steps provide the only external “handle” to control the process (Zuckerman, 2019). Therefore, no cyclical process with a net flux in one direction exists in which only a protein changes through a repeated sequence of conformational states; coupling to an external source of free energy is always necessary.
Finally, it is worth emphasizing that because the transporter protein moves cyclically through different conformations, it is not altered in any permanent way. In the energetic description of the process (see Section 3.2 below), the transporter does not appear. Thus, transporters act as enzymes for moving substrate, similar to how biochemical enzymes catalyze the formation and breaking of chemical bonds. In this sense, transporters are “physical enzymes” or “molecular machines” in that they catalyze a physical process instead of a chemical one. Other proteins of this kind are molecular motors, which turn chemical energy into movement of the protein itself, or rotary pumps such as the V-type and P-type ATPases, which turn chemical energy into rotary motion and movement of protons or ions across the cell membrane; the latter can run in reverse to turn rotary motion by ion flow into chemical bonds. Similarly, transporters run backwards if the concentrations are changed appropriately, which becomes obvious when analyzing the thermodynamic driving forces.
4.3.2. Driving forces
Quantitatively, the only thermodynamic driving forces Xi are the ones originating in electrochemical potential 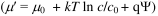 differences of ions and substrates across the cell membrane (Dill and Bromberg, 2003); free energy differences due to the different states of the protein cancel in the whole cycle and play no role (Hill, 1989). The driving force for species i
differences of ions and substrates across the cell membrane (Dill and Bromberg, 2003); free energy differences due to the different states of the protein cancel in the whole cycle and play no role (Hill, 1989). The driving force for species i 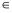 {I,S} is
{I,S} is
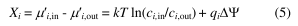
where ci is the concentration (or activity) on the indicated side of the membrane, qi the charge, 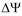 =
= 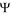 in -
in - 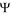 out is the transmembrane potential, T is the temperature and k is Boltzmann’s constant. The membrane potential is typically negative,
out is the transmembrane potential, T is the temperature and k is Boltzmann’s constant. The membrane potential is typically negative, 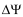 < 0. Thus, for typical driving cations (Na+, H+ with q = +1e) and
< 0. Thus, for typical driving cations (Na+, H+ with q = +1e) and 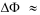 100mV the membrane potential contributes at T = 298 K about qI
100mV the membrane potential contributes at T = 298 K about qI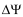
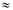 -3.9 kT. Typical sodium concentrations are on the order of 100 mM on the outside and 10 mM inside a cell and hence kT ln cI,in/cI,out = -2.3 kT. If the substrate is neutral (the electrostatic component is zero for qS = 0) then a positive net charge is moved into the cell down an electrostatic potential and a sizable fraction of the available free energy will be provided from the membrane potential component. In general, any electrogenic transport (movement of a net charge) is affected by the membrane potential.
-3.9 kT. Typical sodium concentrations are on the order of 100 mM on the outside and 10 mM inside a cell and hence kT ln cI,in/cI,out = -2.3 kT. If the substrate is neutral (the electrostatic component is zero for qS = 0) then a positive net charge is moved into the cell down an electrostatic potential and a sizable fraction of the available free energy will be provided from the membrane potential component. In general, any electrogenic transport (movement of a net charge) is affected by the membrane potential.
Denote by Ji the flux at which particle i is transported across the membrane (in particles per unit time), with the direction out→in counting as Ji < 0 and the reverse as Ji > 0. Note that in a simple cycle such as the one in Figure 1, exactly one ion is moved for each substrate molecule and hence the absolute values of these fluxes must be the same, |JI| = |JS| but the signs will differ, depending on symport or antiport processes.
When the driving force is negative, e.g., XI < 0, then spontaneous movement occurs, such as influx of the driving ion and hence JI < 0. The antiporter is supposed to move substrate against a gradient from the inside to the outside, i.e., against the opposing driving force XS < 0 under which S particles would spontaneously move into the cell. The rate of free energy dissipation is
 = JIXI + JSXS ≥ 0. (6)
= JIXI + JSXS ≥ 0. (6)
 = 0 holds in equilibrium but then no transport occurs (see Section 3.1). The second law of thermodynamics requires
= 0 holds in equilibrium but then no transport occurs (see Section 3.1). The second law of thermodynamics requires  > 0 in non-equilibrium steady state, i.e., when concentrations remain fixed at their non-equilibrium values and do not change (Hill, 1989). In steady-state, the transporter moves ions and substrates at a constant flux. Under which conditions will the antiporter move S from inside to outside, i.e., given JS > 0 (even though XS < 0), what is required of I? Rearranging Eq. 6
> 0 in non-equilibrium steady state, i.e., when concentrations remain fixed at their non-equilibrium values and do not change (Hill, 1989). In steady-state, the transporter moves ions and substrates at a constant flux. Under which conditions will the antiporter move S from inside to outside, i.e., given JS > 0 (even though XS < 0), what is required of I? Rearranging Eq. 6
JIXI > -JSX








 4, often referred to as leaks or slippage. Such a transition would allow three cycles to become possible: The transport cycle that was just described and two leak cycles: cycle 1
4, often referred to as leaks or slippage. Such a transition would allow three cycles to become possible: The transport cycle that was just described and two leak cycles: cycle 1 
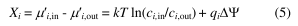
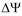
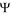
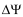
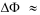 100mV the membrane potential contributes at
100mV the membrane potential contributes at