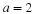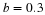Basic MATLAB programming concepts are presented to demonstrate how to create, save and execute script files.
MATLAB provides scripting and automation tools that can simplify repetitive computational tasks. For example, a series of commands executed in a MATLAB session to solve a problem can be saved in a script file called an m-file. An m-file can be executed from the command line by typing the name of the file or by pressing the run button in the built-in text editor tool bar.
A script is a file containing a sequence of MATLAB statements. Script files have a filename extension of .m. By typing the filename at the command prompt, we can run the script and obtain results in the command window.
A sample m-file named ThermalConductivity.m is displayed in Text Editor below. Note the triangle (in green) run button in the tool bar, pressing this button executes the script in the command window.
ThermalConductivity.m file is displayed in Text Editor.
Now let us see how an m-file is created and executed.
A cylindrical acetylene bottle with a radius r=0.3 m has a hemispherical top. The height of the cylindrical part is h=1.5 m. Write a simple script to calculate the volume of the acetylene bottle.
To solve this problem, we will first apply the volume of cylinder equation. Using the volume of sphere equation, we will calculate the volume of hemisphere. The total volume of the acetylene bottle is found with the sum of volumes equation.
To write the script, we will use the built-in text editor. From the menu bar select File > New > Script. The text editor window will open in a separate window. First save this file as AcetyleneBottle.m. In that window type the following code paying attention to the use of percentage and semicolon symbols to comment out the lines and suppress the output, respectively.
% This script computes the volume of an acetylene bottle with a radius r=0.3 m, % a hemispherical top and a height of cylindrical part h=1.5 m. r=0.3; % Radius [m] h=1.5; % Height [m] Vol_top=(2*pi*r^3)/3; % Calculating the volume of hemispherical top [m3] Vol_cyl=pi*r^2*h; % Calculating the volume of cylindrical bottom [m3] Vol_total=Vol_top+Vol_cyl % Calculating the total volume of acetylene bottle [m3]
After running the script by pressing the green button in the Text Editor tool bar, the output is displayed in the command window as shown below.
input Function Notice that the script we have created above is not interactive and computes the total volume only for the variables defined in the m-file. To make this script interactive we will make some changes to the existing AcetyleneBottle.m by adding input function and save it as AcetyleneBottleInteractive.m.
The syntax for input is as follows:
userResponse = input('prompt') Now, let's incorporate the input command in AcetyleneBottleInteractive.m as shown below and the subsequent figure:
% This script computes the volume of an acetylene bottle
% user is prompted to enter
% a radius r for a hemispherical top
% a height h for a cylindrical part
r=input('Enter the radius of acetylene bottle in meters ');
h=input('Enter the height of cylindrical part of acetylene bottle in meters ');
Vol_top=(2*pi*r^3)/3; % Calculating the volume of hemispherical top [m3]
Vol_cyl=pi*r^2*h; % Calculating the volume of cylindrical bottom [m3]
Vol_total=Vol_top+Vol_cyl % Calculating the total volume of acetylene bottle [m3]
The command window upon run will be as follows, note that user keys in the radius and height values and the same input values result in the same numerical answer as in example which proves that the computation is correct.
disp Function As you might have noticed, the output of our script is not displayed in a well-formatted fashion. Using disp, we can control how text or arrays are displayed in the command window. For example, to display a text string on the screen, type in disp('Hello world!'). This command will return our friendly greeting as follows: Hello world!
disp(variable) can be used to display only the value of a variable. To demonstrate this, issue the following command in the command window:
b = [1 2 3 4 5]We have created a row vector with 5 elements. The following is displayed in the command window:
>> b = [1 2 3 4 5]
b =
1 2 3 4 5 Now if we type in disp(b) and press enter, the variable name will not be displayed but its value will be printed on the screen:
>> disp(b)
1 2 3 4 5 The following example demonstrates the usage of disp function.
Now, let's open AcetyleneBottleInteractive.m file and modify it by using the disp command. First save the file as AcetyleneBottleInteractiveDisp.m, so that we don't accidentally introduce errors to a working file and also we can easily find this particular file that utilizes the disp command in the future. The new file should contain the code below:
% This script computes the volume of an acetylene bottle
% user is prompted to enter
% a radius r for a hemispherical top
% a height h for a cylindrical part
clc % Clear screen
disp('This script computes the volume of an acetylene bottle')
r=input('Enter the radius of acetylene bottle in meters ');
h=input('Enter the height of cylindrical part of acetylene bottle in meters ');
Vol_top=(2*pi*r^3)/3; % Calculating the volume of hemispherical top [m3]
Vol_cyl=pi*r^2*h; % Calculating the volume of cylindrical bottom [m3]
Vol_total=Vol_top+Vol_cyl; % Calculating the total volume of acetylene bottle [m3]
disp(' ') % Display blank line
disp('The volume of the acetylene bottle is') % Display text
disp(Vol_total) % Display variableYour screen output should look similar to the one below:
This script computes the volume of an acetylene bottle
Enter the radius of acetylene bottle in meters .3
Enter the height of cylindrical part of acetylene bottle in meters 1.5
The volume of the acetylene bottle is
0.4807num2str Function The num2str function allows us to convert a number to a text string. Basic syntax is str = num2str(A) where variable A is converted to a text and stored in str. Let's see how it works in AcetyleneBottleInteractiveDisp.m. Remember to save the file with a different name before editing it, for example, AcetyleneBottleInteractiveDisp1.m.
Add the following line of code to your file:
str = ['The volume of the acetylene bottle is ', num2str(Vol_total), ' cubic meters.'];
Notice that the three arguments in str are separated with commas. The first argument is a simple text that is contained in ' '. The second argument is where the number to string conversion take place. And finally the third argument is also a simple text that completes the sentence displayed on the screen. Using semicolon at the end of the line suppresses the output. In the next line of our script, we will call str with disp(str);.
AcetyleneBottleInteractiveDisp1.m file should look like this:
% This script computes the volume of an acetylene bottle
% user is prompted to enter
% a radius r for a hemispherical top
% a height h for a cylindrical part
clc % Clear screen
disp('This script computes the volume of an acetylene bottle:')
disp(' ') % Display blank line
r=input('Enter the radius of acetylene bottle in meters ');
h=input('Enter the height of cylindrical part of acetylene bottle in meters ');
Vol_top=(2*pi*r^3)/3; % Calculating the volume of hemispherical top [m3]
Vol_cyl=pi*r^2*h; % Calculating the volume of cylindrical bottom [m3]
Vol_total=Vol_top+Vol_cyl; % Calculating the total volume of acetylene bottle [m3]
disp(' ') % Display blank line
str = ['The volume of the acetylene bottle is ', num2str(Vol_total), ' cubic meters.'];
disp(str);Running the script should produce the following:
This script computes the volume of an acetylene bottle: Enter the radius of acetylene bottle in meters .3 Enter the height of cylindrical part of acetylene bottle in meters 1.5 The volume of the acetylene bottle is 0.48066 cubic meters.
diary Function Instead of writing a script from scratch, we sometimes solve problems in the Command Window as if we are using a scientific calculator. The steps we perform in this fashion can be used to create an m-file. For example, the diary function allows us to record a MATLAB session in a file and retrieve it for review. Reviewing the file and by copying relevant parts of it and pasting them in to an m-file, a script can be written easily.
Typing diary at the MATLAB prompt toggles the diary mode on and off. As soon as the diary mode is turned on, a file called diary is created in the current directory. If you like to save that file with a specific name, say for example problem16, type diary ('problem16'). A file named problem16 will be created. The following is the content of a diary file called problem16. Notice that in that session, the user is executing the four files we created earlier. The user's keyboard input and the resulting display output is recorded in the file. The session is ended by typing diary which is printed in the last line.
AcetyleneBottle
Vol_total =
0.4807
AcetyleneBottleInteractive
Enter the radius of acetylene bottle in meters .3
Enter the height of cylinderical part of acetylene bottle in meters 1.5
Vol_total =
0.4807
AcetyleneBottleInteractiveDisp
This script computes the volume of an acetylene bottle
Enter the radius of acetylene bottle in meters .5
Enter the height of cylinderical part of acetylene bottle in meters 1.6
The volume of the acetylene bottle is
1.5184
AcetyleneBottleInteractiveDisp1
This script computes the volume of an acetylene bottle:
Enter the radius of acetylene bottle in meters .9
Enter the height of cylinderical part of acetylene bottle in meters 1.9
The volume of the acetylene bottle is 6.3617 cubic meters.
diaryTry to apply the following guidelines when writing your scripts:
Share your code or programs with others, consider adopting one of Creative Commons or GNU General Public License schemes
Include your name and contact info in the opening lines
Use comments liberally
Group your code and use proper indentation
Use white space liberally
Use descriptive names for your variables
Use descriptive names for your m-files
A script is a file containing a sequence of MATLAB statements. Script files have a filename extension of .m.
Functions such as input, disp and num2str can be used to make scripts interactive,
diary function is useful to record a MATLAB command window session from which an m-file can be easily created,
Various style guidelines covered here help improve our code.
Problem Set for Introductory Programming
Write a script that will ask for pressure value in psi and display the equivalent pressure in kPa with a statement, such as "The converted pressure is: ..."
% This script converts pressures from psi to kPa
% User is prompted to enter pressure in psi
clc % Clear screen
disp('This script converts pressures from psi to kPa:')
disp(' ') % Display blank line
psi=input('What is the pressure value in psi? ');
kPa=psi*6.894757; % Calculating pressure in kPa
disp(' ') % Display blank line
str = ['The converted pressure is: ', num2str(kPa), ' kPa.'];
disp(str);
The script output is as follows:
This script converts pressures from psi to kPa: What is the pressure value in psi? 150 The converted pressure is: 1034.2135 kPa.
Write a script that generates a table of conversions from Fahrenheit to Celsius temperatures for a range and increment entered by the user, such as
Enter the beginning temperature in F:
Enter the ending temperature in F:
Enter the increment value:
Test your script with 20 the beginning Fahrenheit value, 200 the ending Fahrenheit value and 20 the increment.
% This script generates a table of conversions
% From Fahrenheit to Celsius temperatures
clc % Clear screen
disp('This script generates a table of conversions from Fahrenheit to Celsius')
disp(' ') % Display blank line
lowerF=input('Enter the beginning temperature in F: ');
upperF=input('Enter the ending temperature in F: ');
increment=input('Enter the increment value: ');
Fahrenheit=[lowerF:increment:upperF]; % Creating a row vector with F values
Celsius=5/9*(Fahrenheit-32); % Converting from F to C
disp(' ') % Display blank line
str = ['Fahrenheit Celsius '];% Displaying table header
disp(str);
% Tabulating results in two columns, ' is being used to transpose row to column
disp([Fahrenheit' Celsius'])
The script output is as follows:
This script generates a table of conversions from Fahrenheit to Celsius Enter the beginning temperature in F: 20 Enter the ending temperature in F: 200 Enter the increment value: 20 Fahrenheit Celsius 20.0000 -6.6667 40.0000 4.4444 60.0000 15.5556 80.0000 26.6667 100.0000 37.7778 120.0000 48.8889 140.0000 60.0000 160.0000 71.1111 180.0000 82.2222 200.0000 93.3333
Pascal's Law states that pressure is transmitted undiminished in all directions throughout a fluid at rest. (See the illustration below). An initial force of 150 N is transmitted from a piston of 25 mm^2 to a piston of 100 mm^2. This force is progressively increased up to 200 N. Write a script that computes the corresponding load carried by the larger piston and tabulate your results.
% This script computes the load carried by the larger piston in a hydraulic system
clc % Clear screen
disp('This script computes the load carried by the larger piston in a hydraulic system')
disp(' ') % Display blank line
initialF=150;
finalF=200;
increment=10;
area1=25;
area2=100;
F1=[initialF:increment:finalF]; % Creating a row vector with F1 values
F2=F1*area2/area1; % Calculating F2 values
disp(' ') % Display blank line
str = [' F1 F2 '];% Displaying table header
disp(str);
disp([F1' F2']) % Tabulating results in two columns, ' is being used to transpose row to column
The script output is as follows:
This script computes the load carried by the larger piston in a hydraulic system
F1 F2
150 600
160 640
170 680
180 720
190 760
200 800
Modify your script in previous problem so that the user provides the following input:
Enter the initial force in N:
Enter the final force in N:
Enter the increment value:
Enter the area of small piston in mm^2:
Enter the area of big piston in mm^2:
Test your script with 150, 200, 10, 25 and 100 with respect to each input variable.
% This script computes the load carried by the larger piston in a hydraulic system
clc % Clear screen
disp('This script computes the load carried by the larg